Hello everybody,
I would like to solve numerically this system of PDEs with the following initial conditions: 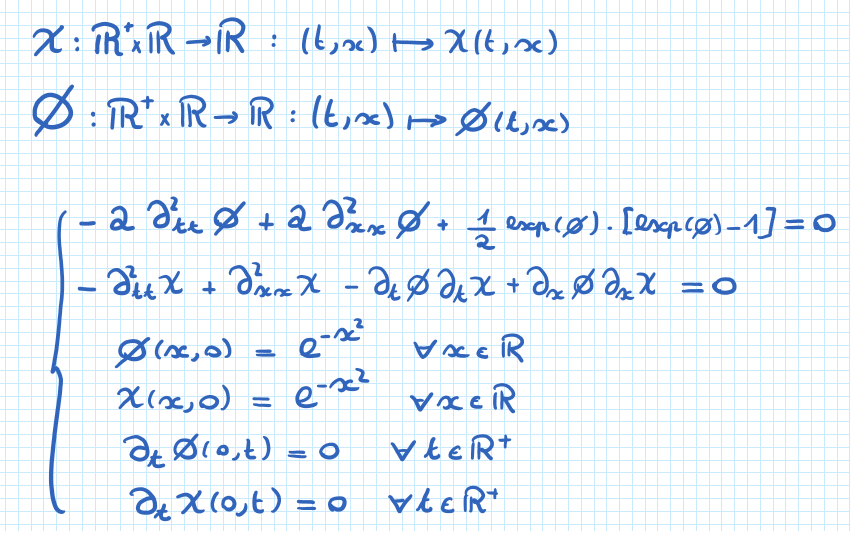
Here is my attempt to do it in Mathematica:
clear[\[Phi], \[Chi]];
sol = NDSolve[{
-2*D[\[Phi][x, t], t, t] +
2 D[\[Phi][x, t], x,
x] + (Exp (\[Phi][x, t])/
2)*((D[\[Chi][x, t], t])^2 - (D[\[Chi][x, t], x])^2) -
Exp[\[Phi][x, t]]*(Exp[\[Phi][x, t]] - 1) == 0,
-D[\[Chi][x, t], t, t] + D[\[Chi][x, t], x, x] -
D[\[Phi][x, t], t]*D[\[Chi][x, t], t] +
D[\[Phi][x, t], x]*D[\[Chi][x, t], x] == 0 ,
\[Phi][x, 0] == Exp[-x^2],
D[\[Phi][0, t], t] == 0,
\[Chi][x, 0] == Exp[-x^2],
D[\[Chi][0, t], t] == 0
},
{\[Phi], \[Chi]}, {x, 0, 10}, {t, 0, 10}];
Plot3D[\[Phi][x, t] /. sol[[1]], {x, 0, 10}, {t, 0, 10}]
Unfortunately it gives me an unexpected error.
I have reread the code many times but I do not find the error.
Can someone help me please?