The clone puzzle was recently popularized by a great YouTube presentation by Zvezdelina Stankova on the Numberphile channel (https://www.youtube.com/watch?v=lFQGSGsXbXE). It serves as a good examples of some key concepts in Mathematics:

• Invariants
• Limits (geometric series)
• Impossibility proofs by contradiction

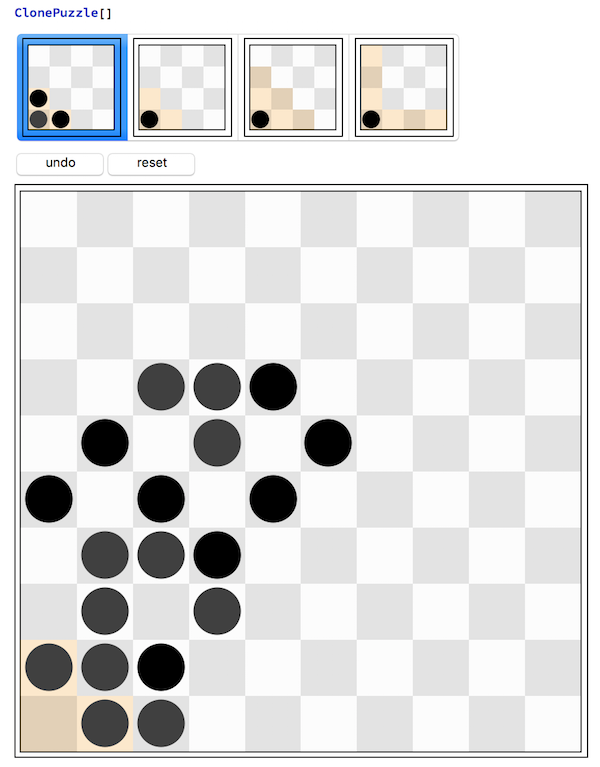
The game starts with three checkers in the lower-left corner of a quarter-infinite chessboard. A move replaces one checker with one each above and to the right of the original. The goal is to get all checkers out of the highlighted jail.

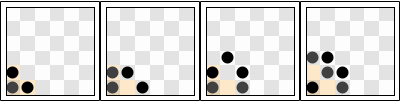
You can try to solve the challenge from any of the proposed initial positions, using the CDF version attached, or the source notebook of this post.

The invariant is constructed by assigning the value 1 to the lower-left square, then each square receives half the value of the square below or to the left. A move will not change the sum of all occupied squares. The total value of the highlighted jail is 2, and the value of the infinite rest of the board is also 2. To win, you would have to fill all squares in the infinite board.

Programming the Clone Puzzle

Each square of the board is a Button[] with the rendering depending dynamically on the board (which is an array of True/False values).

The board will automatically extend when you approach the top or right edges.

I've used a classless object-oriented approach, that attaches all code to a single unique symbol, with object data stored in additional symbols, all created in a Module[]. The constructor has this outline:

makeBoard[size_,initial_List]:=Module[{clone,board, ...},
    board=...;(*array of True/False values *)
    aux[]:=...;
    clone[undo]:=...;
    clone[game]:=...;
    clone]

Methods are of the form clone[meth]. The game is set up as a DynamicModule[] with a menu for the initial positions and undo/reset buttons:

ClonePuzzle[]:=With[{pops=Function[{pos,jail},makeBoard[10,pos,jail]->makeBoard[4,pos,jail][image]]@@@sampleLayouts},
    Clear[board];
    DynamicModule[{board=pops[[1,1]]},
    Column[{
    SetterBar[Dynamic[board],pops],
    Row[{Button["undo",board[undo],Enabled->Dynamic[board[dirty]]],
    Button["reset",board[reset],Enabled->Dynamic[board[dirty]]] },ImageSize->Full],
    Dynamic[board[game]]
    }],SaveDefinitions->True]]

The board rendering creates a table of buttons (in the render[] auxiliary function). The board itself depends only on hits size (dim), which avoids unnecessary dynamic updates.

clone[game]:=
    Deploy[Framed[Dynamic[GraphicsGrid[
        Table[Item[render[i,j],Background->bg[i,j]],{i,dim,1,-1},{j,dim}], Frame->True,ImageSize->Large],
    TrackedSymbols:>{dim}]]
];

Attachments: