Hi,

I try to simulate the equalization/distribution of a fluid within a confined volume. I selected the shallow water equations (Saint-Venant equations) and removed the slope and friction part of the equations. The two equations I use are:

eqn1 =

eqn2 =

With:

w - constant width of the channel
h - height of the water in the channel
u -  flow velocity
t - time
x - longitudinal axis along the channel
g - gravity constant

As boundary condition I use:

boundaryCondition = {u[-1, t] == 0, u[1, t] == 0}

which shall be equivalent to "no flow at x=+-1".

My initial condition is no flow at t=0 anywhere and some hat like distribution of the fluid height between x=-1 ... 1:

initialCondition = {h[x, 0] == 3 + Cos[x*\[Pi]/2]^2, u[x, 0] == 0};

Cos[x*\[Pi]/2]^2: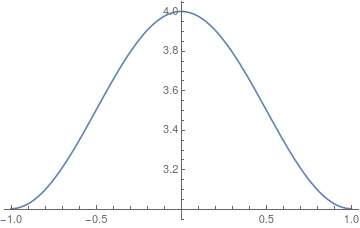

Before solving I assign the remaining constants:

constAssignments = {w -> 1, g -> 9.81};

After that I call NDSolve with the following parameters which unfortunately lead to a warning/error:

sol = NDSolve[{eqn1 /. constAssignments, eqn2 /. constAssignments, 
   initialCondition, boundaryCondition}, {u, h}, {x, -1, 1}, {t, 0, 
   10}]

NDSolve::ndsz: At t == 1.9560944493733925`, step size is effectively zero; singularity or stiff system suspected.
NDSolve::eerr: Warning: scaled local spatial error estimate of 4.424896536902471`*^7 at t = 1.9560944493733925` in the direction of independent variable x is much greater than the prescribed error tolerance. Grid spacing with 25 points may be too large to achieve the desired accuracy or precision. A singularity may have formed or a smaller grid spacing can be specified using the MaxStepSize or MinPoints method options.

A plot of the results with Plot3D[h[x, t] /. sol, {x, -1, 1}, {t, 0, 1.5}] reveals that it looks pretty good for the first tenth of a second but then the result gets disturbed.

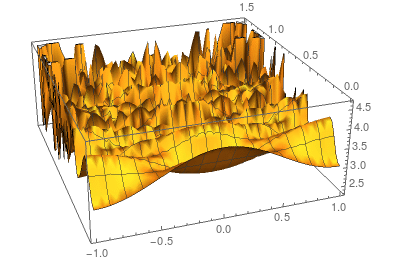
Do you have any suggestion how to solve this issue? I also wonder why DSolve is unable to solve this problem symbolically since the solution should be quite simple. I have attached the notebook file with the problem and some further explanations.

Thank you!

Attachments: