Feb 22, 2009
It appears that the absolute value, minus 1/2, of the limit(integral of (-1)^xx^(1/x) from 1 to 2N as N->infinity) would equal the partial sum of (-1)^xx^(1/x) from 1 to where the upper summation is even and growing without bound. Is anyone interested in improving or disproving this conjecture?
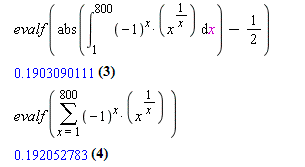
March 12, 2015
What about records of computing the integral analog of the MRB constant? (I call it the MKB constant.) See Google Scholar MKB constant.
Richard Mathar did a lot of work on it here , where M is the MRB constant and M1 is MKB:

M1 (MKB) can be written as and integral of a power of e:
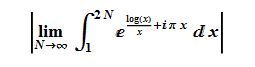
I've gotten Mathematica to compute 125 digits. However, they are not proven to be correct yet! They are
0.68765236892769436980931240936544016493963738490362254179507101010743\
366253478493706862729824049846818873192933433546612328629
. First, we compute the real part as far as Mathematica will allow.
a1 = NIntegrate[Cos[x Pi] x^(1/x), {x, 1, Infinity},
WorkingPrecision -> 100]
0.07077603931152880353952802183028200136575469620336299759658471973672\
987938741600037745028756981434374
a2 = NIntegrate[Cos[x Pi] x^(1/x), {x, 1, Infinity},
WorkingPrecision -> 120]
a2 - a1
0.07077603931152880353952802183028200136575469620336302758317278266053\
31986618615110244568060496758380620699811570793175408
2.998658806292380331927444551064700651847986149432*10^-53
a3 = NIntegrate[Cos[x Pi] x^(1/x), {x, 1, Infinity},
WorkingPrecision -> 150]
a3 - a2
0.07077603931152880353952802183028200136575469620336302758317278816361\
8457264385970709799491401005081151056924116255307801983594127144525095\
5653544005192
5.5030852586025244596853426853513292430889869429591759902612*10^-63
a4 = NIntegrate[Cos[x Pi] x^(1/x), {x, 1, Infinity},
WorkingPrecision -> 200]
a4 - a3
0.07077603931152880353952802183028200136575469620336302758317278816361\
8457264382036580831881266177238210031756216795402920795214039271485948\
634659563768084109747493815003439875479076850383786911941519465
-3.9341289676101348278429410251678994599048811883800878730391469306948\
367511*10^-78
a5 = NIntegrate[Cos[x Pi] x^(1/x), {x, 1, Infinity},
WorkingPrecision -> 250]
a5 - a4
0.07077603931152880353952802183028200136575469620336302758317278816361\
8457264382036580831881266177238209440733969109717926999044694539086929\
3857095687266500964737783523859835124762555195276023702167529617039725\
7261177753806842756198742365511173334813888
-5.9102224768568499379616934473239901924894999504143401327371546261745\
6363002821330856184541724766503*10^-103
Next, we compute the imaginary part to the same precision.
b1 = NIntegrate[I Sin[x Pi] x^(1/x), {x, 1, Infinity},
WorkingPrecision -> 100] - I/Pi
0.*10^-117 -
0.6840003894379321291827444599926611267109914826550016181302726087470\
544306934833279937664708191960468 I
b2 = NIntegrate[I Sin[x Pi] x^(1/x), {x, 1, Infinity},
WorkingPrecision -> 120] - I/Pi
b2 - b1
0.*10^-137 -
0.6840003894379321291827444599926611267109914826549994343226304054256\
46767722886537984405858512438464223325361496951820797 I
0.*10^-117 +
2.1838076422033214076629705967900093606123067575826*10^-51 I
b3 = NIntegrate[I Sin[x Pi] x^(1/x), {x, 1, Infinity},
WorkingPrecision -> 150] - I/Pi
b3 - b2
0.*10^-167 -
0.6840003894379321291827444599926611267109914826549994343226303771381\
5305812568206208637713014270949108628424796532117557865488349026349505\
4352728287677 I
0.*10^-137 +
2.8287493709597204475898028728369728973137041113531630645218*10^-62 I
b4 = NIntegrate[I Sin[x Pi] x^(1/x), {x, 1, Infinity},
WorkingPrecision -> 200] - I/Pi
b4 - b3
0.*10^-218 -
0.6840003894379321291827444599926611267109914826549994343226303771381\
5305812497663815095983421272147867735031056071869477552727290571462108\
208123698276619850397331432861469605963724235550107655309644965 I
0.*10^-167 +
7.0542393541729592998801240893393740460248080312761058454887397227149\
1304910*10^-76 I
b5 = NIntegrate[I Sin[x Pi] x^(1/x), {x, 1, Infinity},
WorkingPrecision -> 250] - I/Pi
b5 - b4
0.*10^-268 -
0.6840003894379321291827444599926611267109914826549994343226303771381\
5305812497663815095983421272147867223796451609148860995867828496814126\
9810848570299802270095261060286697622600207986034863822997401942304753\
4951409792726050072747412751162199808963072 I
0.*10^-218 +
5.1123460446272061655685946207464798122703884124663962338780532683279\
9843703703436946621273009904771*10^-102 I
b6 = NIntegrate[I Sin[x Pi] x^(1/x), {x, 1, Infinity},
WorkingPrecision -> 300] - I/Pi
b6 - b5
0.*10^-318 -
0.6840003894379321291827444599926611267109914826549994343226303771381\
5305812497663815095983421272147867223796451609148860995867804988314557\
9408739051911924508290758754789975176921766748245229306743723292030351\
1357229649514450909272015113199881208930542548540913212596310791355732\
04151474091653439098975 I
0.*10^-268 +
2.3508499569040210951838787776180450230549672244567844123778963451625\
36786502744023594180143211599163475397637962318600032530*10^-127 I
Notice that WorkingPrecision->100 gave 51 consistent (correct) digits, WorkingPrecision->120 gave 62 correct digits, WorkingPrecision->150 gave 76 correct digits, WorkingPrecision->200 gave 102 correct digits, so it is not too much of a stretch to believe WorkingPrecision->250 gave 125 correct digits.
In[78]:= c = N[Abs[a5 + b5], 125]
Out[78]= 0.\
6876523689276943698093124093654401649396373849036225417950710101074336\
6253478493706862729824049846818873192933433546612328629
April 18, 2015
Going back to integral analog of the MRB constant'
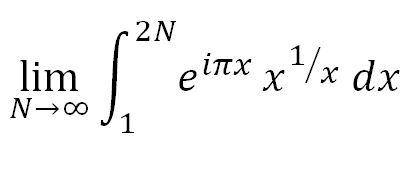 :
:
Using formula 5 on page 3 of http://arxiv.org/pdf/0912.3844v3.pdf
.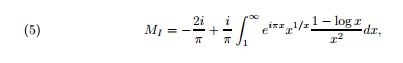
We can compute plenty of digits of the integral analog of the MRB constant' (I once called it the MKB constant, named after Marsha Kell-Burns my, now ex, wife.) In the paper, Mathar simply calls it M1.
Until further notice in this post when we compute the imaginary part of M1, we will be concerned with the imaginary part's absolute value only,
This time we will compute the Imaginary part first to at least 500 digits:
a[1] = 0; For[n = 1, n < 11,
a[n] = N[2/Pi -
1/Pi*NIntegrate[
Cos[Pi*x]*x^(1/x)*(1 - Log[x])/x^2, {x, 1, Infinity},
WorkingPrecision -> 100*n], 50 n]; Print[a[n] - a[n - 1]],
n++]; Print[a[11]]
\
giving
0.6840003894379321291827444599926611267109914826549994343226303771381530581249766381509598342127214787
0.*10^-101
0.*10^-151
0.*10^-201
0.*10^-251
0.*10^-301
0.*10^-351
0.*10^-401
0.*10^-451
0.*10^-501
0.6840003894379321291827444599926611267109914826549994343226303771381530581249766381509598342127214786722379645160914886099586780498831455794087390519118879988351918366211827085883779918191195794251385436100844782462528597869421390620796113023053439642582325892202911183326091512210367124716901047132601108752764946385830438156754378694878046808312868541961166205744280461776232345922905313658259576212809654022016030244583148587352474339130505540080799774619683572540292971258866450201101870835703060314349396491402064932644813564545345219868887520120
. Likewise the real part:
b[1] = 0; For[n = 1, n < 11,
b[n] = N[-1/Pi*
NIntegrate[Sin[Pi*x]*x^(1/x)*(1 - Log[x])/x^2, {x, 1, Infinity},
WorkingPrecision -> 100*n], 50 n]; Print[b[n] - b[n - 1]],
n++]; Print[b[11]]
giving
0.07077603931152880353952802183028200136575469620336302758317278816361845726438203658083188126617723821
0.*10^-102
0.*10^-152
0.*10^-202
0.*10^-252
0.*10^-302
0.*10^-352
0.*10^-402
0.*10^-452
0.*10^-502
0.07077603931152880353952802183028200136575469620336302758317278816361845726438203658083188126617723820944073396910971792699904464538475364292258443860652193330471222906120205483985764336623434898438270710499897053952312269178485299032185072743545220051257328105422174249313177670295863771714489658779291185716175115405623656039914848817528200250723061535734571065031458992196831648681239079549382556509741967588147362548743205919028695774572411439927516593391029992733107982746794845130889328251307263102570083031527430861023428334369104098217022622689
. Then the magnitude:
N[Sqrt[a[11]^2 + b[11]^2], 500]
giving
0.68765236892769436980931240936544016493963738490362254179507101010743\
3662534784937068627298240498468188731929334335466123286287665409457565\
9577211580255650416284625143925097120589697986500952590195706813170472\
5387265069668971286335322245474865156721299946377659227025219748069576\
0895993932096027520027641920489863095279507385793449828250341732295653\
3809181101532087948181335825805498812728097520936901677028741356923292\
2644964771090329726483682930417491673753430878118054062296678424687465\
624513174205
. That checks with the 200 digits computed by the quadosc command in mpmath by FelisPhasma at https://github.com/FelisPhasma/MKB-Constant .The function is defined here: http://mpmath.googlecode.com/svn/trunk/doc/build/calculus/integration.html#oscillatory-quadrature-quadosc

P.S.
I just now finished 750 digits, (about the max with formula 5 from the paper, as far as Mathematica is concerned).
Here is the work:
a[1] = 0; For[n = 1, n < 16,
a[n] = N[2/Pi -
1/Pi*NIntegrate[
Cos[Pi*x]*x^(1/x)*(1 - Log[x])/x^2, {x, 1, Infinity},
WorkingPrecision -> 100*n], 50 n]; Print[a[n] - a[n - 1]],
n++]; Print[a[16]];
b[1] = 0; For[n = 1, n < 16,
b[n] = N[-1/Pi*
NIntegrate[Sin[Pi*x]*x^(1/x)*(1 - Log[x])/x^2, {x, 1, Infinity},
WorkingPrecision -> 100*n], 50 n]; Print[b[n] - b[n - 1]],
n++]; Print[b[16]]; Print[N[Sqrt[a[16]^2 + b[16]^2], 750]]
0.6840003894379321291827444599926611267109914826549994343226303771381530581249766381509598342127214787
0.*10^-101
0.*10^-151
0.*10^-201
0.*10^-251
0.*10^-301
0.*10^-351
0.*10^-401
0.*10^-451
0.*10^-501
0.*10^-551
0.*10^-601
3.*10^-650
-4.*10^-700
-2.6*10^-749
0.68400038943793212918274445999266112671099148265499943432263037713815\
3058124976638150959834212721478672237964516091488609958678049883145579\
4087390519118879988351918366211827085883779918191195794251385436100844\
7824625285978694213906207961130230534396425823258922029111833260915122\
1036712471690104713260110875276494638583043815675437869487804680831286\
8541961166205744280461776232345922905313658259576212809654022016030244\
5831485873524743391305055400807997746196835725402929712588664502011018\
7083570306031434939649140206493264481356454534521986888752011950353818\
1776359577265099302389566135475579468144849763261779452665955246258699\
8679271659049208654746533234375478909962633090080006358213908728990850\
5026759549928935029206442637425786005036048098598304092996753145589012\
64547453361707037686708654522699
0.07077603931152880353952802183028200136575469620336302758317278816361845726438203658083188126617723821
0.*10^-102
0.*10^-152
0.*10^-202
0.*10^-252
0.*10^-302
0.*10^-352
0.*10^-402
0.*10^-452
0.*10^-502
2.*10^-551
-1.*10^-600
1.8*10^-650
1.27*10^-699
4.34*10^-749
0.07077603931152880353952802183028200136575469620336302758317278816361\
8457264382036580831881266177238209440733969109717926999044645384753642\
9225844386065219333047122290612020548398576433662343489843827071049989\
7053952312269178485299032185072743545220051257328105422174249313177670\
2958637717144896587792911857161751154056236560399148488175282002507230\
6153573457106503145899219683164868123907954938255650974196758814736254\
8743205919028695774572411439927516593391029992733107982746794845130889\
3282513072631025700830315274308610234283343691040982170226226904594029\
7055093272952022662549075225941956559080574835998923469310063614655255\
0629713179601483134045038416878054929072981851045829413286377842843667\
5378730394247519728064887287780998671021887797977772522419765594172569\
277490031071938177749184834961300
0.687652368927694369809312409365440164939637384903622541795071010107433662534784937068627298240498468188731929334335466123286287665409457565957721158025565041628462514392509712058969798650095259019570681317047253872650696689712863353222454748651567212999463776592270252197480695760895993932096027520027641920489863095279507385793449828250341732295653380918110153208794818133582580549881272809752093690167702874135692329226449647710903297264836829304174916737534308781180540622966784246874656245131742049004832216427665542900559350289936114782223424261285828326467186036500189315374147638489679365569122714398706519530651330568884655048857998738535162606116788633540389660052822237449082894798620397228331715198160243676576563833057235963591510865254600
Using formula 7 from http://arxiv.org/pdf/0912.3844v3.pdf,
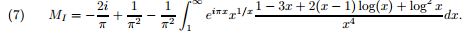 .
.
(Treating it as we did formula 5), First, the imaginary part to at least 1000 digits::
a[1] = 0; For[n = 1, n < 21,
a[n] = N[2/Pi +
1/Pi^2 NIntegrate[
Sin[x Pi] x^(1/x) (1 - 3 x + 2 (x - 1) Log[x] + Log[x]^2)/
x^4, {x, 1, Infinity}, WorkingPrecision -> 100 n], 50 n];
Print[a[n] - a[n - 1]], n++]; Print[a[21]]
0.6840003894379321291827444599926611267109914826549994343226303771381530581249766381509598342127214787
0.*10^-101
0.*10^-151
0.*10^-201
0.*10^-251
0.*10^-301
0.*10^-351
0.*10^-401
0.*10^-451
0.*10^-501
0.*10^-551
0.*10^-601
0.*10^-651
0.*10^-701
0.*10^-751
0.*10^-801
0.*10^-851
0.*10^-901
-2.*10^-950
5.*10^-1000
0.684000389437932129182744459992661126710991482654999434322630377138153058124976638150959834212721478672237964516091488609958678049883145579408739051911887998835191836621182708588377991819119579425138543610084478246252859786942139062079611302305343964258232589220291118332609151221036712471690104713260110875276494638583043815675437869487804680831286854196116620574428046177623234592290531365825957621280965402201603024458314858735247433913050554008079977461968357254029297125886645020110187083570306031434939649140206493264481356454534521986888752011950353818177635957726509930238956613547557946814484976326177945266595524625869986792716590492086547465332343754789099626330900800063582139087289908505026759549928935029206442637425786005036048098598304092996753145589012645474533617070376867086545228223060940434935219252885333298390272342234952870883304116640409421452765284609364941205344122569781634782508368641126766528707019957340895061936246645065753101916781254557006989818409283317145837167345971516970849116096077030635788389165381066055992688
Then the real part to at least 1000 digits:
b[1] = 0; For[n = 1, n < 21,
b[n] = N[1/Pi^2 -
1/Pi^2 NIntegrate[
Cos[Pi x] x^(1/x) (1 - 3 x + 2 (x - 1) Log[x] + Log[x]^2)/
x^4, {x, 1, Infinity}, WorkingPrecision -> 100 n], 50 n];
Print[b[n] - b[n - 1]], n++]; Print[b[21]]
0.07077603931152880353952802183028200136575469620336302758317278816361845726438203658083188126617723821
0.*10^-102
0.*10^-152
0.*10^-202
0.*10^-252
0.*10^-302
0.*10^-352
0.*10^-402
0.*10^-452
0.*10^-502
0.*10^-552
0.*10^-602
0.*10^-652
0.*10^-702
0.*10^-752
0.*10^-802
0.*10^-852
-3.*10^-901
8.*10^-951
-4.6*10^-1000
0.0707760393115288035395280218302820013657546962033630275831727881636184572643820365808318812661772382094407339691097179269990446453847536429225844386065219333047122290612020548398576433662343489843827071049989705395231226917848529903218507274354522005125732810542217424931317767029586377171448965877929118571617511540562365603991484881752820025072306153573457106503145899219683164868123907954938255650974196758814736254874320591902869577457241143992751659339102999273310798274679484513088932825130726310257008303152743086102342833436910409821702262269045940297055093272952022662549075225941956559080574835998923469310063614655255062971317960148313404503841687805492907298185104582941328637784284366753787303942475197280648872877809986710218877979777725224197655941725692774900310719381777491848349627938468198411955193898347075098152638657614980900350262780319142430252921925131515239611841070722530473939496294305264627977744876814858325335947117076721493110160508928494597906728688873533031986215124467678736429981544321187124269147141804397293341613
Then the magnitude:
In[97]:= N[Sqrt[a[21]^2 + b[21]^2], 1000]
Out[97]= 0.\
6876523689276943698093124093654401649396373849036225417950710101074336\
6253478493706862729824049846818873192933433546612328628766540945756595\
7721158025565041628462514392509712058969798650095259019570681317047253\
8726506966897128633532224547486515672129994637765922702521974806957608\
9599393209602752002764192048986309527950738579344982825034173229565338\
0918110153208794818133582580549881272809752093690167702874135692329226\
4496477109032972648368293041749167375343087811805406229667842468746562\
4513174204900483221642766554290055935028993611478222342426128582832646\
7186036500189315374147638489679365569122714398706519530651330568884655\
0488579987385351626061167886335403896600528222374490828947986203972283\
3171519816024367657656383305723596359151086525460036387486837632622334\
2987257095524637683005910353149353985736118868884201748241906260834981\
7303422370398413326428269921074045506558966667483453656748906071577744\
4147548424388220133662816274116986724576330176058912438027319979840883\
05950589130911719199
PPS. I just now finished a 1500 digit computation of the integral analog of the MRB constant, but I don't have any way of checking it other than to see that it confirms smaller computations. Which thing it does.
In[99]:= aa =
N[2/Pi + 1/Pi^2 NIntegrate[
Sin[x Pi] x^(1/x) (1 - 3 x + 2 (x - 1) Log[x] + Log[x]^2)/
x^4, {x, 1, Infinity}, WorkingPrecision -> 3000], 1500]
Out[99]= 0.\
6840003894379321291827444599926611267109914826549994343226303771381530\
5812497663815095983421272147867223796451609148860995867804988314557940\
8739051911887998835191836621182708588377991819119579425138543610084478\
2462528597869421390620796113023053439642582325892202911183326091512210\
3671247169010471326011087527649463858304381567543786948780468083128685\
4196116620574428046177623234592290531365825957621280965402201603024458\
3148587352474339130505540080799774619683572540292971258866450201101870\
8357030603143493964914020649326448135645453452198688875201195035381817\
7635957726509930238956613547557946814484976326177945266595524625869986\
7927165904920865474653323437547890996263309008000635821390872899085050\
2675954992893502920644263742578600503604809859830409299675314558901264\
5474533617070376867086545228223060940434935219252885333298390272342234\
9528708833041166404094214527652846093649412053441225697816347825083686\
4112676652870701995734089506193624664506575310191678125455700698981840\
9283317145837167345971516970849116096077030635788389165381066055992708\
4284702473154303800276803908560080204997803241058414188902018357202062\
9532415382916822796942734253441520784640814155687968986766443021927163\
6249354786973717955004441549085673392105556692081075647388204227896978\
1483978754685921758294318270385312597177598977912650715548994562461701\
1553879109152932039370312241134127950112036269188660519350584627066913\
4925878278209048717316088629321353274101519307401594635990058104175474\
300641475776727955287474213040
In[98]:= bb =
N[1/Pi^2 -
1/Pi^2 NIntegrate[
Cos[Pi x] x^(1/x) (1 - 3 x + 2 (x - 1) Log[x] + Log[x]^2)/
x^4, {x, 1, Infinity}, WorkingPrecision -> 3000], 1500]
Out[98]= 0.\
0707760393115288035395280218302820013657546962033630275831727881636184\
5726438203658083188126617723820944073396910971792699904464538475364292\
2584438606521933304712229061202054839857643366234348984382707104998970\
5395231226917848529903218507274354522005125732810542217424931317767029\
5863771714489658779291185716175115405623656039914848817528200250723061\
5357345710650314589921968316486812390795493825565097419675881473625487\
4320591902869577457241143992751659339102999273310798274679484513088932\
8251307263102570083031527430861023428334369104098217022622690459402970\
5509327295202266254907522594195655908057483599892346931006361465525506\
2971317960148313404503841687805492907298185104582941328637784284366753\
7873039424751972806488728778099867102188779797777252241976559417256927\
7490031071938177749184834962793846819841195519389834707509815263865761\
4980900350262780319142430252921925131515239611841070722530473939496294\
3052646279777448768148583253359471170767214931101605089284945979067286\
8887353303198621512446767873642998154432118712426914714180439729334146\
8345902382977472975053271988386946291215512340931334841526712825988330\
6521193975174379922254198045615178994412133135553490942451521573377205\
4086429300485891441696490339106907723915822537813700713422515725943626\
7756749980892097547020923938358076198570370106085596863039832425037481\
4946826330552459256977035009973219582010379262683780372730214991685800\
3676611833579648850161974289307066295385292264148146789532534018500663\
1153014589399140567464592864024
In[109]:= c1500 = Sqrt[aa^2 + bb^2]
Out[109]= \
0.68765236892769436980931240936544016493963738490362254179507101010743\
3662534784937068627298240498468188731929334335466123286287665409457565\
9577211580255650416284625143925097120589697986500952590195706813170472\
5387265069668971286335322245474865156721299946377659227025219748069576\
0895993932096027520027641920489863095279507385793449828250341732295653\
3809181101532087948181335825805498812728097520936901677028741356923292\
2644964771090329726483682930417491673753430878118054062296678424687465\
6245131742049004832216427665542900559350289936114782223424261285828326\
4671860365001893153741476384896793655691227143987065195306513305688846\
5504885799873853516260611678863354038966005282223744908289479862039722\
8331715198160243676576563833057235963591510865254600363874868376326223\
3429872570955246376830059103531493539857361188688842017482419062608349\
8173034223703984133264282699210740455065589666674834536567489060715777\
4441475484243882201336628162741169867245763301760589124380273199798408\
8305950589130911719198776146941477264898934365742508503405073273852990\
3546587114217499635584514475429656959327732862489935076490012861232249\
2446704232200904844779690044774489466704342791971033325818579375177198\
9865742583276770011926585495711579480114327818546199372349313180236079\
1389248808154759564302727311223193005229640892474022665093207969297797\
9723087954832182561714039165214592519432072341006090867558444590500046\
6707963346545638317950978935794173691635274461184852166407791838662429\
40408834876470623546535579027725
Mathar gives a simple scheme to find better formulas at http://arxiv.org/pdf/0912.3844v3.pdf . I could use some help in programming it: (I keep getting erroneous results!) Does anyone get the right results here?

Below, where the upper limit of the following integrals shows Infinity, it is meant to be the (Ultraviolet limit of the sequence) as mentioned by Mathar here:
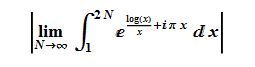
Until further notice in this post when we compute the imaginary part of M1, we will be concerned with the imaginary part's absolute value only,
I derived a new formula for computing the integral analog of the MRB constant':
f[x_]:=x^(1/x);-((2 I)/\[Pi]^3) + 1/\[Pi]^2 - (
2 I)/\[Pi] + (I/Pi)^3*
Integrate[(-1)^x*D[f[x], {x, 3}], {x, 1, Infinity}]
In the traditional form that is M1=
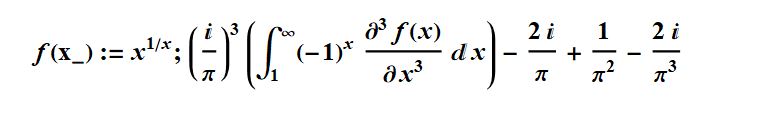
Using it I computed 2000 digits in only 10.8 minutes:
In[131]:= Timing[f[x_] = x^(1/x);
a = N[1/\[Pi]^2 + (1/Pi)^3*
NIntegrate[Sin[Pi*x]*D[f[x], {x, 3}], {x, 1, Infinity},
WorkingPrecision -> 4000], 2000];
b = N[2/\[Pi]^3 +
2/\[Pi] + (1/Pi)^3*
NIntegrate[Cos[Pi x]*D[f[x], {x, 3}], {x, 1, Infinity},
WorkingPrecision -> 4000], 2000];
Print[N[Sqrt[a^2 + b^2], 2000]]]
During evaluation of In[131]:= 0.68765236892769436980931240936544016493963738490362254179507101010743366253478493706862729824049846818873192933433546612328628766540945756595772115802556504162846251439250971205896979865009525901957068131704725387265069668971286335322245474865156721299946377659227025219748069576089599393209602752002764192048986309527950738579344982825034173229565338091811015320879481813358258054988127280975209369016770287413569232922644964771090329726483682930417491673753430878118054062296678424687465624513174204900483221642766554290055935028993611478222342426128582832646718603650018931537414763848967936556912271439870651953065133056888465504885799873853516260611678863354038966005282223744908289479862039722833171519816024367657656383305723596359151086525460036387486837632622334298725709552463768300591035314935398573611886888420174824190626083498173034223703984133264282699210740455065589666674834536567489060715777444147548424388220133662816274116986724576330176058912438027319979840883059505891309117191987761469414772648989343657425085034050732738529903546587114217499635584514475429656959327732862489935076490012861232249244670423220090484477969004477448946670434279197103332581857937517719898657425832767700119265854957115794801143278185461993723493131802360791389248808154759564302727311223193005229640892474022665093207969297797972308795483218256171403916521459251943207234100609086755844459050004667079633465456383179509789357941736916352744611848521664077918386624294040883487647062354653558109265769644276994369741555722263494599492834558291937955573706480722982389806312472239746286527176248883116124285469947303667188075506826507811479428582807366599407544908560990699866167233307144245764835741501174979679166078765231145175411199825822532170091858833628202128777966026600647843068442894310401343003939117236867245656732686719139206716028255819141802331701942027248337771633882445225049334329008827371320849006472846226868011129149192754883153995560921671208059671732704499253517327447921147157
Out[131]= {653.145, Null}
I am presently computing 10,000 digits using that formula. Come back here for results!
That formula didn't work out; I will try one of the following formulas.
Here are 2 more, more advanced formulas; remember f(x) is x^(1/x):
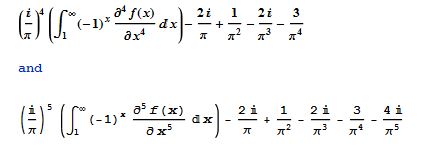
I did finish a 5,000 digit computation using M1=
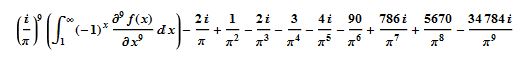
in 48.11 minutes.
Here are the 5000 digits:of the magnitude:
0.68765236892769436980931240936544016493963738490362254179507101010743366253478493706862729824049846818873192933433546612328628766540945756595772115802556504162846251439250971205896979865009525901957068131704725387265069668971286335322245474865156721299946377659227025219748069576089599393209602752002764192048986309527950738579344982825034173229565338091811015320879481813358258054988127280975209369016770287413569232922644964771090329726483682930417491673753430878118054062296678424687465624513174204900483221642766554290055935028993611478222342426128582832646718603650018931537414763848967936556912271439870651953065133056888465504885799873853516260611678863354038966005282223744908289479862039722833171519816024367657656383305723596359151086525460036387486837632622334298725709552463768300591035314935398573611886888420174824190626083498173034223703984133264282699210740455065589666674834536567489060715777444147548424388220133662816274116986724576330176058912438027319979840883059505891309117191987761469414772648989343657425085034050732738529903546587114217499635584514475429656959327732862489935076490012861232249244670423220090484477969004477448946670434279197103332581857937517719898657425832767700119265854957115794801143278185461993723493131802360791389248808154759564302727311223193005229640892474022665093207969297797972308795483218256171403916521459251943207234100609086755844459050004667079633465456383179509789357941736916352744611848521664077918386624294040883487647062354653558109265769644276994369741555722263494599492834558291937955573706480722982389806312472239746286527176248883116124285469947303667188075506826507811479428582807366599407544908560990699866167233307144245764835741501174979679166078765231145175411199825822532170091858833628202128777966026600647843068442894310401343003939117236867245656732686719139206716028255819141802331701942027248337771633882445225049334329008827371320849006472846226868011129149192754883153995560921671208059671732704499253517327447529208297180672654123457301218758892278525894167935930983363218877512533994251978272092700003994136520699813263053327399132641690231179063314931546906927612775633995348209911166678724589467821767106592498663827057034363632241807121831546175498178011687284590439293322231263406301066863589072717290630291441982684113819198880100231182613587798104863611185433976009254862585527222843445901958943153561148829083242874018226480554274231391324767376148485531787767908124831873688579979114662856184612164534836370699371440464263768724668291617743681719766849740663590277737977490693183461320266666793472116774276618408124767965369796362732668987556797338128876129264558867657737417548617146808592137056879602982206609613881069490166381528825180204703315896719667069923077454352649723496033985893188309150391579573916059639453655188856334980355047281560296288150836680499821806918067869468571687709518088408966653716009356556714281694904914038988996962213833530636987279769672200413448893419914190954063100962251649102614676944333201213024711868954772741991675045198246947499574872027800654821823797116399297131866662866832215332914761325880983081211272181775518951539503852063119472301382766303820851467743266039356123495461914463960644386394228342211998370152351720235034997434035743513051754761571835043769475528640144621307760159481496713401409374957729200400650100318226988524015127382509490642900236553851499823658269458873976032051355393161653806016080446394196719312454167915154602448638624354575153334932298393406734174580316934939632892851077461038399470015366439910136971186909599331204517462262508377673477745789645309425145559198802530351403897927622891172233239135167420567162398873965477371498335087310395422796362380227536212159184529243644094285328763286873653399867593200891823468738537356817916009007206857590792983184556882143118383332812491747733056313117179696094921120670802012310012864110800437831852620698327457619035904268498030693438632685623213366864129523404256345542376567721287706234359125016588483777876970236084456277023948551334490591022594253744077631232660869593809453087749830900393202787736482133628148979992109544954840067942735030391105496026321872468122542495017023785810605820545392820104069279893067324597299043883381251767370331206913429284614563732308018369972360638019778425246546329838131639355043236388708044857300408692365733932897876809202025693305332974091411983635619038514442263783801745983300121464879550146672827072002317686396598587702487509572349422593441184802476344187280014450860069307120621758277552124841158659386176036703247124389223327008210072318671884895179305778728051888524412158486781863155034447221379906386062559915129172725833420555901857729690605950941678587057025641848365090809750870051863842805803189784976076099574956436664131457150096711473033060684065060747340764998195621425524824611657787212347497307297184843276100338110267863618974154272345482369968216663233417338501929114697679974461999040589290327155974468087040862022522065912789
I'm getting closer to 10K digits of M1: Using 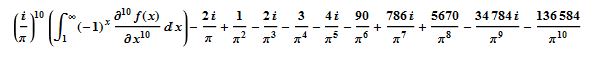 , where f(x)=x^(1/x).
, where f(x)=x^(1/x).
I got approx. 10K digits of the imaginary part, but the real part was a little garbled.
Finally using
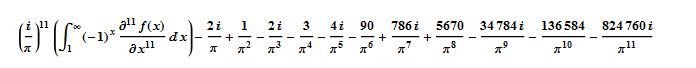 , where f(x) = x^(1/x) ,
, where f(x) = x^(1/x) ,
.I got about 10000 digits of M1 in about 12 hours. (It showed that the 5000 digit computation was only correct to 4979 digits, though.) Here is a rough program to get it:
f[x_]:=x^(1/x); Print[DateString[]]; Print[T0 = SessionTime[]]; prec = 10000;
Timing[Print[
a = N[Re[-(136584/Pi^10) - (34784*I)/Pi^9 +
5670/Pi^8 + (786*I)/Pi^7 - 90/Pi^6 -
(4*I)/Pi^5 - 3/Pi^4 - (2*I)/Pi^3 +
1/Pi^2 - (2*I)/Pi] -
(1/Pi)^10*
NIntegrate[Cos[Pi*x]*D[f[x], {x, 10}], {x, 1, Infinity},
WorkingPrecision -> prec,
PrecisionGoal -> prec], prec]];
Print[SessionTime[] - T0, " seconds"];
Print[
N[b = -Im[-(136584/Pi^10) - (34784*I)/Pi^9 +
5670/Pi^8 + (786*I)/Pi^7 - 90/Pi^6 -
(4*I)/Pi^5 - 3/Pi^4 - (2*I)/Pi^3 +
1/Pi^2 - (2*I)/Pi] +
(1/Pi)^10*
NIntegrate[Sin[Pi*x]*D[f[x], {x, 10}], {x, 1, Infinity},
WorkingPrecision -> prec,
PrecisionGoal -> prec], prec]]]; Print[
SessionTime[] - T0, " seconds"];
Print[N[Sqrt[a^2 + b^2], prec]]; Print[DateString[]];
See attached 10000MKB.pdf and 10KMKB.nb for work and digits.
On May 5, I computed another 10,000 digits in 9.55 hours see attached faster10KMKB.
On May 6, I computed another 10,000 digits in a blistering fast 5.1 hours see attached fastest10KMKB.nb.
On May 9, I improved that timing to 4.8 hours (17355 seconds). Here is the code I used:
d = 15; f[x_] = x^(1/x); ClearAll[a, b, h];
h[n_] := Sum[
StirlingS1[n, k]*Sum[(-j)^(k - j)*Binomial[k, j], {j, 0, k}], {k, 1,
n}]; h[0] = 1; g =
2 I/Pi - Sum[-I^(n + 1) h[n]/Pi^(n + 1), {n, 1, d}]; Print[
DateString[]];
Print[T0 = SessionTime[]]; prec = 10000;
Print[N[a = -Re[g] + (1/Pi)^(d + 1)*
NIntegrate[
Simplify[Cos[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"];
Print[N[b =
Im[g] - (1/Pi)^(d + 1)*
NIntegrate[
Simplify[Sin[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"]; Print[
N[Sqrt[a^2 + b^2], prec]]; Print[DateString[]];
April 20, 2015
FelisPhasma has been helpful in providing me with a little competition in computing the integral analog of the MRB constant. See https://github.com/FelisPhasma/MKB-Constant.
I've never done this before. But I so much would like to see others breaking these records that I'm going to give away a program that is practically guaranteed to break my record of 10,000 digits, for the integral analog of the MRB constant in a day or so. The program could use some "clean up" if you care to go that far. (The imaginary part is given as a positive, real constant: it actually starts with a negative sign and of course ends with I.)
Here it is:
f[x_] = x^(1/x); Print[DateString[]]; Print[
T0 = SessionTime[]]; prec = 11000; Timing[
Print[a =
N[Re[(633666648 I)/\[Pi]^13 -
33137280/\[Pi]^12 - ((824760 I)/\[Pi]^11) -
136584/\[Pi]^10 - (34784 I)/\[Pi]^9 +
5670/\[Pi]^8 + (786 I)/\[Pi]^7 - 90/\[Pi]^6 - (4 I)/\[Pi]^5 -
3/\[Pi]^4 - (2 I)/\[Pi]^3 +
1/\[Pi]^2 - (2 I)/\[Pi]] + (1/Pi)^12*
NIntegrate[Cos[Pi x]*D[f[x], {x, 12}], {x, 1, Infinity},
WorkingPrecision -> prec, PrecisionGoal -> prec], prec]];
Print[SessionTime[] - T0, " seconds"];
Print[N[b = -Im[(633666648 I)/\[Pi]^13 -
33137280/\[Pi]^12 - ((824760 I)/\[Pi]^11) -
136584/\[Pi]^10 - (34784 I)/\[Pi]^9 +
5670/\[Pi]^8 + (786 I)/\[Pi]^7 + 90/\[Pi]^6 - (4 I)/\[Pi]^5 -
3/\[Pi]^4 - (2 I)/\[Pi]^3 +
1/\[Pi]^2 - (2 I)/\[Pi]] - (1/Pi)^13*
NIntegrate[Cos[Pi x]*D[f[x], {x, 13}], {x, 1, Infinity},
WorkingPrecision -> prec, PrecisionGoal -> prec],
prec]]]; Print[SessionTime[] - T0, " seconds"]; Print[
N[Sqrt[a^2 + b^2], prec]]; Print[DateString[]];
Will anyone let me know you are running this program to break my record?
Edit: On Sat 2 May 2015 19:03:45 I started a 15,000 digit, new record computation of the real and imaginary parts and magnitude of the integral analog of the MRB constant, (where the imaginary part is given as a positive, real constant), using the following code.
f[x_] = x^(1/x); ClearAll[a];
h[n_] := Sum[
StirlingS1[n, k]*Sum[(-j)^(k - j)*Binomial[k, j], {j, 0, k}], {k, 1,
n}]; h[0] = 1; g = -2 I/Pi +
Sum[-I^(n + 1) h[n]/Pi^(n + 1), {n, 1, 18}]; Print[DateString[]];
Print[T0 = SessionTime[]]; prec = 15000;
Print[N[a =
Re[g] + (1/Pi)^19*
NIntegrate[
Simplify[Sin[Pi*x]*D[f[x], {x, 19}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"];
Print[N[b = -Im[g] + (1/Pi)^19*
NIntegrate[
Simplify[Cos[Pi*x]*D[f[x], {x, 19}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"]; Print[
N[Sqrt[a^2 + b^2], prec]]; Print[DateString[]];
The formula behind this computation is 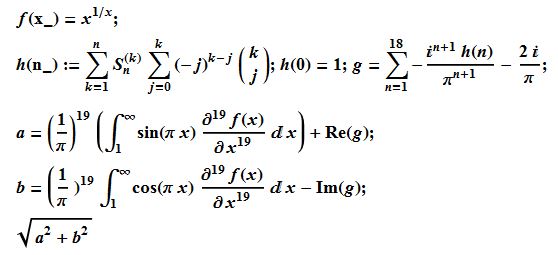
Edit: The program took 33.75 hours, The full run is attached in 15KMKB3.nb.
Edit May 9, 2015: I better than halved my time! I computed 15000 digits in 14.83 hours. See fastestMKB15K.nb/. The faster formula is
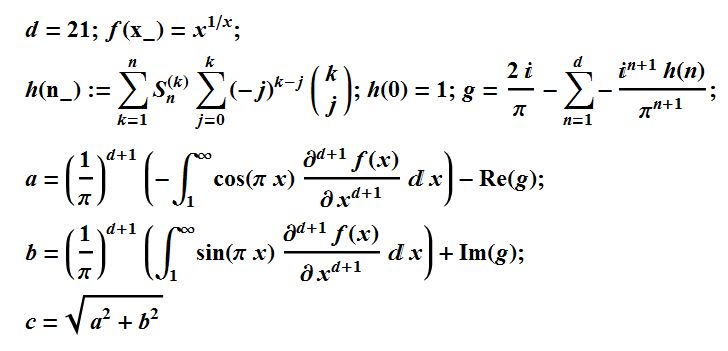
If you still want me to write out a code for more digits, for you to break that record, let me know.
May 11, 2015
Still talking about the integral analog of the MRB constant: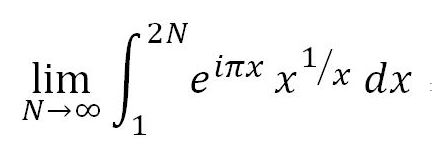
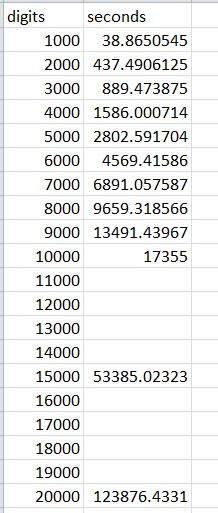
Here are my speed records -- can you beat any of them?
Here is a graph of those speed records with a trendline:

The 20,000 digit run is attached as MKB20K.nb, and MKB20K.pdf,
Here is the algorithm used:
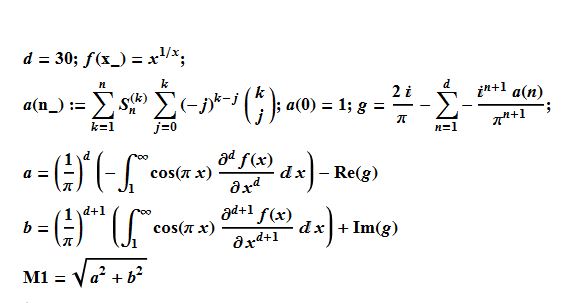
Here is the code:
d = 30; f[x_] = x^(1/x); ClearAll[a, b, h];
a[n_] := Sum[
StirlingS1[n, k]*Sum[(-j)^(k - j)*Binomial[k, j], {j, 0, k}], {k, 1,
n}]; a[0] = 1; g =
2 I/Pi - Sum[-I^(n + 1) a[n]/Pi^(n + 1), {n, 1, d}]; Print[
DateString[]];
Print[T0 = SessionTime[]]; prec = 20000;
Print[N[a = -Re[g] - (1/Pi)^(d)*
NIntegrate[
Simplify[Cos[Pi*x]*D[f[x], {x, d}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"];
Print[N[b =
Im[g] + (1/Pi)^(d + 1)*
NIntegrate[
Simplify[Cos[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"]; Print[
N[Sqrt[a^2 + b^2], prec]]; Print[DateString[]];
I just now completed a 25,000 digit computation. It took 63.7 hours and confirmed the 20,000 digits. I updated MKB20K.nb and MKB20K.pdf. Here is the algorithm and the code I used:
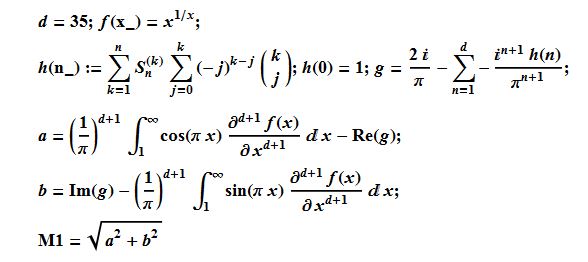
d = 35; f[x_] = x^(1/x); ClearAll[a, b, h];
h[n_] := Sum[
StirlingS1[n, k]*Sum[(-j)^(k - j)*Binomial[k, j], {j, 0, k}], {k, 1,
n}]; h[0] = 1; g =
2 I/Pi - Sum[-I^(n + 1) h[n]/Pi^(n + 1), {n, 1, d}]; Print[
DateString[]];
Print[T0 = SessionTime[]]; prec = 25000;
Print[N[a = -Re[g] + (1/Pi)^(d + 1)*
NIntegrate[
Simplify[Cos[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"];
Print[N[b =
Im[g] - (1/Pi)^(d + 1)*
NIntegrate[
Simplify[Sin[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"]; Print[
N[Sqrt[a^2 + b^2], prec]]; Print[DateString[]];
Here is new a graph of those speed records with a trendline: 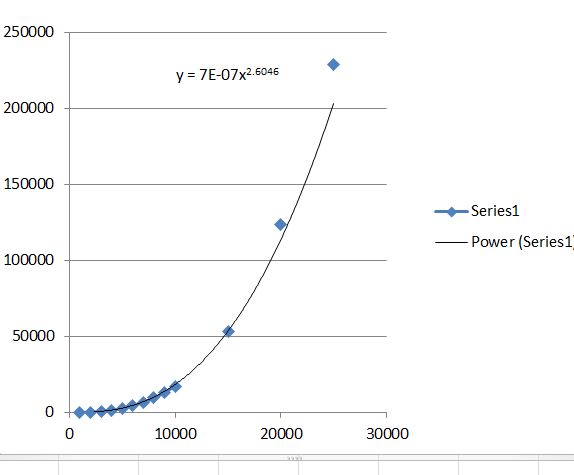
Edit:
On Tue 26 May 2015 06:21:00, I started a 30,000 digit computation using the following code.
Does anyone else want to try to break the record?
$MaxExtraPrecision = 100; d = 43; f[x_] = x^(1/x); ClearAll[a, b, h];
h[n_] := Sum[
StirlingS1[n, k]*Sum[(-j)^(k - j)*Binomial[k, j], {j, 0, k}], {k, 1,
n}]; h[0] = 1; g =
2 I/Pi - Sum[-I^(n + 1) h[n]/Pi^(n + 1), {n, 1, d}]; Print[
DateString[]];
Print[T0 = SessionTime[]]; prec = 30000;
Print[N[a = -Re[g] + (1/Pi)^(d + 1)*
NIntegrate[
Simplify[Cos[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"];
Print[N[b =
Im[g] - (1/Pi)^(d + 1)*
NIntegrate[
Simplify[Sin[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"]; Print[
N[Sqrt[a^2 + b^2], prec]]; Print[DateString[]];
Edit: My first full 30,0000 run finished on Sun 31 May 2015 00:45:09.
Time span: {"4.767 days", "114.4 hours", "6864 minutes", "411849 seconds"} See attached MKB30K2.nb worksheet.
Here is an updated speed record plot, with a trendline. (I think the 30,000 digit run can be done faster.)
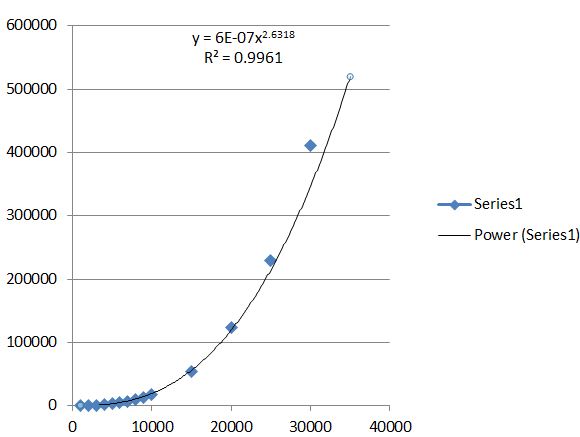
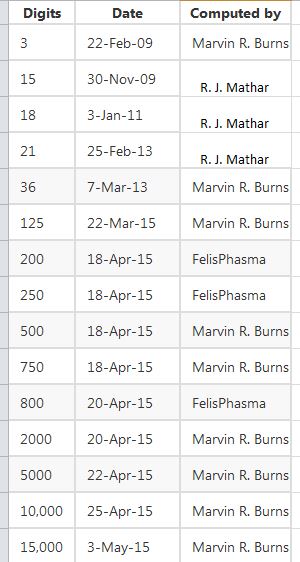
Here is an extensive record of records of computing the integral analog of the MRB constant:
![enter image description here][62]
Here is a graph of those records. (The progression of computed digits is so extreme, it is almost unbelievable!) 
6
June 5, 2015
I think I came up with a rough program that computes any "prec" digits of the integral analog of the MRB constant. It chooses, d, the best (or close to the best) order of derivative to use in Mathar's algorithm mentioned in a previous post (formula (12) at http://arxiv.org/pdf/0912.3844v3.pdf ), Then uses the appropriate code that integrates the integral analog of the constant. It shows the real and imaginary parts as positive real constants and the value the integral and gives some timings. It could use a lot of cleanups! I hope someone can help me test it with varying values of prec. Please reply with your intentions to use it and the results. If no one else can clean it up I will after I tested it more.
prec = 2000; d = Ceiling[0.264086 + 0.00143657 prec]; If[
Mod[d, 4] == 0, f[x_] = x^(1/x); ClearAll[a, b, h];
a[n_] :=
Sum[StirlingS1[n, k]*
Sum[(-j)^(k - j)*Binomial[k, j], {j, 0, k}], {k, 1, n}]; a[0] = 1;
g = 2 I/Pi - Sum[-I^(n + 1) a[n]/Pi^(n + 1), {n, 1, d}];
Print[DateString[]];
Print[T0 = SessionTime[]];
Print[N[a = -Re[g] - (1/Pi)^(d + 1)*
NIntegrate[
Simplify[Sin[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"];
Print[N[b =
Im[g] - (1/Pi)^(d + 1)*
NIntegrate[
Simplify[Cos[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"];
Print[N[Sqrt[a^2 + b^2], prec]]; Print[DateString[]];,
If[Mod[d, 4] == 1, f[x_] = x^(1/x); ClearAll[a, b, h];
h[n_] :=
Sum[StirlingS1[n, k]*
Sum[(-j)^(k - j)*Binomial[k, j], {j, 0, k}], {k, 1, n}];
h[0] = 1; g = 2 I/Pi - Sum[-I^(n + 1) h[n]/Pi^(n + 1), {n, 1, d}];
Print[DateString[]];
Print[T0 = SessionTime[]];
Print[N[
a = -Re[g] - (1/Pi)^(d + 1)*
NIntegrate[
Simplify[Cos[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"];
Print[N[
b = Im[g] + (1/Pi)^(d + 1)*
NIntegrate[
Simplify[Sin[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"];
Print[N[Sqrt[a^2 + b^2], prec]]; Print[DateString[]];,
If[Mod[d, 4] == 2, f[x_] = x^(1/x); ClearAll[a, b, h];
a[n_] :=
Sum[StirlingS1[n, k]*
Sum[(-j)^(k - j)*Binomial[k, j], {j, 0, k}], {k, 1, n}];
a[0] = 1; g = 2 I/Pi - Sum[-I^(n + 1) a[n]/Pi^(n + 1), {n, 1, d}];
Print[DateString[]];
Print[T0 = SessionTime[]];
Print[N[
a = -Re[g] - (1/Pi)^(d)*
NIntegrate[
Simplify[Cos[Pi*x]*D[f[x], {x, d}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"];
Print[N[
b = Im[g] + (1/Pi)^(d + 1)*
NIntegrate[
Simplify[Cos[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"];
Print[N[Sqrt[a^2 + b^2], prec]]; Print[DateString[]];,
If[Mod[d, 4] == 3, f[x_] = x^(1/x); ClearAll[a, b, h];
h[n_] :=
Sum[StirlingS1[n, k]*
Sum[(-j)^(k - j)*Binomial[k, j], {j, 0, k}], {k, 1, n}];
h[0] = 1; g = 2 I/Pi - Sum[-I^(n + 1) h[n]/Pi^(n + 1), {n, 1, d}];
Print[DateString[]];
Print[T0 = SessionTime[]];
Print[
N[a = -Re[g] + (1/Pi)^(d + 1)*
NIntegrate[
Simplify[Cos[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"];
Print[
N[b = Im[g] - (1/Pi)^(d + 1)*
NIntegrate[
Simplify[Sin[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"];
Print[N[Sqrt[a^2 + b^2], prec]]; Print[DateString[]];]]]]
Here are some of my best timings to compare with the program's results:
digits seconds
1000 38.8650545
2000 437.4906125
3000 889.473875
4000 1586.000714
5000 2802.591704
6000 4569.41586
7000 6891.057587
8000 9659.318566
9000 13491.43967
10000 17355
11000
12000
13000
14000
15000 53385.02323
16000
17000
18000
19000
20000 123876.4331
21000
22000
23000
24000
25000 229130.3088
26000
27000
28000
29000
30000 411848.6322
Edit: On Fri 5 Jun 2015 20:41:45 I started a 35,000 digit computation with the above "automated" program.
Edit: The 35,000 digit computation should be done by 10:24:38 am EDT | Sunday, June 14, 2015. In the above "automated" program I forgot to adjust the MaxExtraPrecision, but that shouldn't affect the accuracy in that program. It already computed the real part of the integral to 35,000 digits and the first 30,000 of those are the same as the real part of my previously mentioned 30,000 digit calculation. I will keep you posted.
Edit: The 35,000 digit computation finished on Sun 14 Jun 2015 06:52:29, taking 727844 seconds. It is attached as 35KMKB.nb. The first 30,000 digits of those are the same as the ones of my previously mentioned 30,000 digit calculation. (That shows the computation didn't take any "wild" turns because of the lack of MaxExtraPrecision.) Further, it is a good check of the 30,000 digit run, as all of the bigger computations are of the smaller because they all are calculated with distinct formulas using different orders of the derivative of x^(1/x).
Feb 28, 2016
For 2000 digits Mathematica 10. 2.0 shows some remarkable improvement over 10.1.2 with the above "automated program" for computing the digits of the integral analog of the MRB constant.
I will post some speed records that are strictly what the program produces in V 10.2.0, below, no picking and choosing of the methods by a human being. Some results will naturally be slower than my previously mentioned speed records, because I tried so very many methods and recorded only the fastest results.
digits seconds
2000 256.3853590
3000 794.4361122
4000 1633.5822870
5000 2858.9390025
10000 17678.7446323
20000 121431.1895170
40000 I got error msg
to be continued
I have to change the program for 40,000 digits! I'll post the new program when I get 40,000 to work.
As of Wed 29 Jul 2015 11:40:10, one of my computers was happily and busily churning away at 40,000 digits of the integral analog of the MRB constant, using the following formula.
Edit: Mathematica crashed at 11:07 PM 8/4/2016
(I used MKB as a symbol for the integral analog because it is called the MKB constant. You can find the name MKB constant at http://www.ebyte.it/library/educards/constants/MathConstants.html .) If you can weed through my code, at the bottom of this reply, you might want to check the formula for the placement of pluses, minuses, and imaginary units!!! A little hint when checking if the formula matches the code, d is 80 so Mod[d,4] =0.
f[x_] = x^(1/x) : a[n_] :=
Sum[StirlingS1[n, k]*
Sum[(-j)^(k - j)*Binomial[k, j], {j, 0, k}], {k, 1, n}]; a[0] = 1;
g = 2 I/Pi - Sum[-I^(n + 1) a[n]/Pi^(n + 1), {n, 1, 80}]
MKB = -g + (I/Pi)^81*
Integrate[f[x]*D[f[x], {x, 81}], {x, 1, Infinity}]
Here is the code,cleaned up a little: This is the version from Aug 6, 2015 452 pm; for the first time the imaginary part is signed and shown to be multiplied by the imaginary unit!
Block[{$MaxExtraPrecision = 200}, prec = 4000; f[x_] = x^(1/x);
ClearAll[a, b, h];
Print[DateString[]];
Print[T0 = SessionTime[]];
If[prec > 35000, d = Ceiling[0.002 prec],
d = Ceiling[0.264086 + 0.00143657 prec]];
h[n_] :=
Sum[StirlingS1[n, k]*
Sum[(-j)^(k - j)*Binomial[k, j], {j, 0, k}], {k, 1, n}];
h[0] = 1;
g = 2 I/Pi - Sum[-I^(n + 1) h[n]/Pi^(n + 1), {n, 1, d}];
sinplus1 :=
NIntegrate[
Simplify[Sin[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)];
cosplus1 :=
NIntegrate[
Simplify[Cos[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)];
middle := Print[SessionTime[] - T0, " seconds"];
end := Module[{}, Print[SessionTime[] - T0, " seconds"];
Print[c = Abs[a + b]]; Print[DateString[]]];
If[Mod[d, 4] == 0,
Print[N[a = -Re[g] - (1/Pi)^(d + 1)*sinplus1, prec]];
middle;
Print[N[b = -I (Im[g] - (1/Pi)^(d + 1)*cosplus1), prec]];
end];
If[Mod[d, 4] == 1,
Print[N[a = -Re[g] - (1/Pi)^(d + 1)*cosplus1, prec]];
middle;
Print[N[b = -I (Im[g] + (1/Pi)^(d + 1)*sinplus1), prec]]; end];
If[Mod[d, 4] == 2,
Print[N[a = -Re[g] + (1/Pi)^(d + 1)*sinplus1, prec]];
middle;
Print[N[b = -I (Im[g] + (1/Pi)^(d + 1)*cosplus1), prec]];
end];
If[Mod[d, 4] == 3,
Print[N[a = -Re[g] + (1/Pi)^(d + 1)*cosplus1, prec]];
middle;
Print[N[b = -I (Im[g] - (1/Pi)^(d + 1)*sinplus1), prec]];
end];]
Come back to see if I decided whether to try the 40K run again.
EDIT: It looks like I've only got one more test for the program (if it passes) before I retry the 40,000 digit calculation!
EDIT: On Thu 6 Aug 2015 17:23:18, I restarted the 40K run with Windows 10.
EDIT: My first thought was the program took up too much RAM, apparently over 115 GB! ( I have 64GB installed and a 51 GB paging file; nevertheless, Windows 10 closed the Mathematica kernel to keep the computer from losing data. Can someone else try the 40K run on their computer? It should take 2 weeks on a fast one. Please let me know if you try it and let me know the results, so I will know I don't have a problem with my computer., If two weeks is too great of a commitment, can you try taking note on the RAM used for two progressively larger runs, like 20K and 30 K? I will do the same, and we can compare notes. Thank You!
EDIT: I've been monitoring memory usage for smaller runs and found the program only uses minimal memory! This makes the action of Windows 10 (closing Mathematica kernel to avoid data loss) all the more a mystery! Could the 40K run really use up all of that RAM?
I know there are quite a few of you viewing this post; however, is anyone out there working on these calculations?.
Aug 10, 2016
V. 11 is about 1.25 times faster than my newest program for calculating MKB, (the integral analog of the MRB sum). V 10. 4 calculated 20,000 digits in 121431.1895170 seconds and V 11 did it in 96979.6545388 seconds. I've got a little more testing to do, (about 1 day's worth), then I'll try 40,000 digits again, which should take about 12 days. I will post all my updates here, so you might want to save this message as a favorite so you won't lose it.
Update 1
The 40 K automatically started against my wishes on Thu 11 Aug 2016 15:42:08, (due to my pasting two codes at once). I'll keep you informed, how it goes.
Update 2
Windows 10 is pushing an update. Wednesday is the latest it will let me restart. I will restart now with all the updates I can get, Then deffer further ones and hopefully get 12 restart free days to do my 40K.
Update 3
I ran all the updates I could find, differed further ones and restarted 40K on Sun 14 Aug 2016 10:32:40.
Update 4
Widows 10 stopped the calculation! AGAIN! Can anyone else try it and see if you get anywhere? Here is my latest code:
(*Other program:For large calculations.Tested for 1000-35000 digits-- \
see post at \
http://community.wolfram.com/groups/-/m/t/366628?p_p_auth=KA7y1gD4 \
and search for "analog" to find pertinent replies.Designed to include \
40000 digits.A157852 is saved as c,the real part as a and the \
imaginary part as b.*)Block[{$MaxExtraPrecision = 200},
prec = 40000(*Replace 40000 with number of desired digits.40000 \
digits should take two weeks on a 3.5 GH Pentium processor.*);
f[x_] = x^(1/x);
ClearAll[a, b, h];
Print[DateString[]];
Print[T0 = SessionTime[]];
If[prec > 35000, d = Ceiling[0.002 prec],
d = Ceiling[0.264086 + 0.00143657 prec]];
h[n_] :=
Sum[StirlingS1[n, k]*
Sum[(-j)^(k - j)*Binomial[k, j], {j, 0, k}], {k, 1, n}];
h[0] = 1;
g = 2 I/Pi - Sum[-I^(n + 1) h[n]/Pi^(n + 1), {n, 1, d}];
sinplus1 :=
NIntegrate[
Simplify[Sin[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)];
cosplus1 :=
NIntegrate[
Simplify[Cos[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)];
middle := Print[SessionTime[] - T0, " seconds"];
end := Module[{}, Print[SessionTime[] - T0, " seconds"];
Print[c = Abs[a + b]]; Print[DateString[]]];
If[Mod[d, 4] == 0,
Print[N[a = -Re[g] - (1/Pi)^(d + 1)*sinplus1, prec]];
middle;
Print[N[b = -I (Im[g] - (1/Pi)^(d + 1)*cosplus1), prec]];
end];
If[Mod[d, 4] == 1,
Print[N[a = -Re[g] - (1/Pi)^(d + 1)*cosplus1, prec]];
middle;
Print[N[b = -I (Im[g] + (1/Pi)^(d + 1)*sinplus1), prec]]; end];
If[Mod[d, 4] == 2,
Print[N[a = -Re[g] + (1/Pi)^(d + 1)*sinplus1, prec]];
middle;
Print[N[b = -I (Im[g] + (1/Pi)^(d + 1)*cosplus1), prec]];
end];
If[Mod[d, 4] == 3,
Print[N[a = -Re[g] + (1/Pi)^(d + 1)*cosplus1, prec]];
middle;
Print[N[b = -I (Im[g] - (1/Pi)^(d + 1)*sinplus1), prec]];
end];] (*Marvin Ray Burns,Aug 06 2015*)
Sometime in 2017,
To try to get windows 10 from closing Mathematica during the computation I tried the instructions found at https://www.autoitscript.com/forum/topic/177749-stopping-windows-10-from-auto-closing-programs-to-free-up-ram/ . I will record progress in this spot as I did before.
UPDATE I followed the memory usage on my computer and it did use around 64 GB of RAM. And then Windows closed down the Mathematica kernel. I assume that If I can ever afford to maximize my RAM to its 128GB limit the computation will be successful!
Anyone have better luck?
Nov 2017
Concentrating on integral analog of the MRB constant:
Search "integral analog" in the above messages for the understanding of the integral analog of the MRB constant. And search "For 2000 digits Mathematica 10. 2.0" for my history of calculating 40,000 digits of it.
. The basic program I wrote to calculate the Integral analog of the MRB constant is
(*Other program:For large calculations.Tested for 1000-35000 digits-- \
see post at \
http://community.wolfram.com/groups/-/m/t/366628?p_p_auth=KA7y1gD4 \
and search for "analog" to find pertinent replies.Designed to include \
40000 digits.A157852 is saved as c,the real part as a and the \
imaginary part as b.*)Block[{$MaxExtraPrecision = 200},
prec = 40000(*Replace 40000 with number of desired digits.40000 \
digits should take two weeks on a 3.5 GH Pentium processor.*);
f[x_] = x^(1/x);
ClearAll[a, b, h];
Print[DateString[]];
Print[T0 = SessionTime[]];
If[prec > 35000, d = Ceiling[0.264086 + 0.0017 prec],
d = Ceiling[0.264086 + 0.00143657 prec]];
h[n_] :=
Sum[StirlingS1[n, k]*
Sum[(-j)^(k - j)*Binomial[k, j], {j, 0, k}], {k, 1, n}];
h[0] = 1;
g = 2 I/Pi - Sum[-I^(n + 1) h[n]/Pi^(n + 1), {n, 1, d}];
sinplus1 :=
NIntegrate[
Simplify[Sin[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)];
cosplus1 :=
NIntegrate[
Simplify[Cos[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)];
middle := Print[SessionTime[] - T0, " seconds"];
end := Module[{}, Print[SessionTime[] - T0, " seconds"];
Print[c = Abs[a + b]]; Print[DateString[]]];
If[Mod[d, 4] == 0,
Print[N[a = -Re[g] - (1/Pi)^(d + 1)*sinplus1, prec]];
middle;
Print[N[b = -I (Im[g] - (1/Pi)^(d + 1)*cosplus1), prec]];
end];
If[Mod[d, 4] == 1,
Print[N[a = -Re[g] - (1/Pi)^(d + 1)*cosplus1, prec]];
middle;
Print[N[b = -I (Im[g] + (1/Pi)^(d + 1)*sinplus1), prec]]; end];
If[Mod[d, 4] == 2,
Print[N[a = -Re[g] + (1/Pi)^(d + 1)*sinplus1, prec]];
middle;
Print[N[b = -I (Im[g] + (1/Pi)^(d + 1)*cosplus1), prec]];
end];
If[Mod[d, 4] == 3,
Print[N[a = -Re[g] + (1/Pi)^(d + 1)*cosplus1, prec]];
middle;
Print[N[b = -I (Im[g] - (1/Pi)^(d + 1)*sinplus1), prec]];
end];] (*Marvin Ray Burns,
I think I found out why the integral analog of the MRB constant is so hard to calculate to prec=40000 digits! I've been using too high of an order of the derivative of x^(1/x). I've been running out of memory because of using the 80th derivative from d = Ceiling[0.002 prec], because the 58th derivative from Ceiling[0.264086 + 0.00143657 prec] was apparently too small leaving an error statement. I just now asked myself, why make such a big jump? When my big computer gets back from its tuneup I think I will try Ceiling[0.00146 prec] = 59th derivative.
EDIT
I tried Ceiling[0.00146 prec] and Ceiling[0.00145 prec] in Mathematica 11.0 and lost the kernel both times after 6 - 12 hours!
I'm now trying Ceiling[0.0017 prec] with v 10.4. It's been over 12 hours and I've not lost the kernel yet. Wish me luck!
EDIT
I got the following error message and a real part that does not agree with previous computations.
"NIntegrate failed to converge to prescribed accuracy after 9 recursive bisections in x near {x} = {<<42008>>}. NIntegrate obtained -<<42012>> and <<42014>> for the integral and error estimates."
I'm now trying Ceiling[0.0018 prec] with v 10.4....
Ceiling[0.0018 prec] with v 10.4 gave the same error.
I'm working on a new program that uses less memory; stay tuned!
March 13, 2018
I'm now trying Ceiling[0.0019 prec] with v 11.2...., on Mon 12 Mar 2018 05:40:13 Here is a record of the memory used by the program. At times the computer may use significantly more.
"Mon 12 Mar 2018 10:30:00" 14 GB DDR3 RAM
"Mon 12 Mar 2018 13:00:00" 15 GB DDR3 RAM
"Mon 12 Mar 2018 14:00:00" 16 GB DDR3 RAM
"Mon 12 Mar 2018 14:30:00" 17 GB DDR3 RAM
"Mon 12 Mar 2018 15:00:00" 18 GB DDR3 RAM
"Mon 12 Mar 2018 22:30:00" 24 GB DDR3 RAM
"Mon 12 Mar 2018 24:00:00" 26 GB DDR3 RAM
"Tue 13 Mar 2018 06:30:00" 33 GB DDR3 RAM
"Tue 13 Mar 2018 07:30:00" 14 GB DDR3 RAM
"Tue 13 Mar 2018 08:00:00" 15 GB DDR3 RAM
"Tue 13 Mar 2018 08:30:00" 16 GB DDR3 RAM
"Tue 13 Mar 2018 11:30:00" 19 GB DDR3 RAM
"Tue 13 Mar 2018 12:00:00" 20 GB DDR3 RAM
"Tue 13 Mar 2018 14:00:00" 22 GB DDR3 RAM
"Tue 13 Mar 2018 14:30:00" 5 GB DDR3 RAM
"Tue 13 Mar 2018 15:00:00" 6 GB DDR3 RAM
"Tue 13 Mar 2018 16:30:00" 8 GB DDR3 RAM
"Tue 13 Mar 2018 18:30:00" 11 GB DDR3 RAM
"Tue 13 Mar 2018 19:30:00" 13 GB DDR3 RAM
"Tue 13 Mar 2018 20:30:00" 14 GB DDR3 RAM
"Tue 13 Mar 2018 21:00:00" 8 GB DDR3 RAM
"Tue 13 Mar 2018 21:30:00" 11 GB DDR3 RAM
"Wed 14 Mar 2018 07:30:00" 26 GB DDR3 RAM
"Wed 14 Mar 2018 07:30:00" 26 GB DDR3 RAM
"Wed 14 Mar 2018 08:00:00" 25 GB DDR3 RAM.Total used by programs 44.54 GB DDR3 RAM.
"Wed 14 Mar 2018 20:00:00" 37 GB DDR3 RAM.Total used by programs 40.32 GB DDR3 RAM.
"Thu 15 Mar 2018 08:00:00" 0 GB DDR3 RAM.Total used by programs 3.84 GB DDR3 RAM.
Update:
V 11.2 cut off its kernel sometime between "Mon 14 Mar 2018 20:00:00" and "Mon 15 Mar 2018 08:00:00."
It seems to me that V11 under Windows 10 cuts off my RAM-intensive operations.
The last success I had was using V10.2 under Windows 7. I am trying that combination again, this time for the 40 k digits. Below is the code I used then and am using now. At first, I just changed only "prec=35000" to "prac=40000" and got an errant answer for the real part. And I got memory use starting out at
"Thu 15 Mar 2018 08:53:47" 0.3 GB, total computer use 3.84 GB
"Thu 15 Mar 2018 11:48:47" 04.3 GB, total computer use 7.68 GB
"Thu 15 Mar 2018 13:00:00" 01.3 GB, total computer use 5.12 GB
"Thu 15 Mar 2018 14:00:00" 01.3 GB, total computer use 5.12 GB
So now I also changed the coefficient of prec from "d = Ceiling[0.264086 + 0.00143657 prec]" to "d = Ceiling[ 0.002 prec]." I think I can get by with .002 because 10.3 in Windows 7 seems to use less memory that the V 11's in Windows 10.
prec = 40000; d = Ceiling[0.002 prec]; If[Mod[d, 4] == 0,
f[x_] = x^(1/x); ClearAll[a, b, h];
a[n_] :=
Sum[StirlingS1[n, k]*
Sum[(-j)^(k - j)*Binomial[k, j], {j, 0, k}], {k, 1, n}]; a[0] = 1;
g = 2 I/Pi - Sum[-I^(n + 1) a[n]/Pi^(n + 1), {n, 1, d}];
Print[DateString[]];
Print[T0 = SessionTime[]];
Print[N[a = -Re[g] - (1/Pi)^(d + 1)*
NIntegrate[
Simplify[Sin[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"];
Print[N[b =
Im[g] - (1/Pi)^(d + 1)*
NIntegrate[
Simplify[Cos[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"];
Print[N[Sqrt[a^2 + b^2], prec]]; Print[DateString[]];,
If[Mod[d, 4] == 1, f[x_] = x^(1/x); ClearAll[a, b, h];
h[n_] :=
Sum[StirlingS1[n, k]*
Sum[(-j)^(k - j)*Binomial[k, j], {j, 0, k}], {k, 1, n}];
h[0] = 1; g = 2 I/Pi - Sum[-I^(n + 1) h[n]/Pi^(n + 1), {n, 1, d}];
Print[DateString[]];
Print[T0 = SessionTime[]];
Print[N[
a = -Re[g] - (1/Pi)^(d + 1)*
NIntegrate[
Simplify[Cos[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"];
Print[N[
b = Im[g] + (1/Pi)^(d + 1)*
NIntegrate[
Simplify[Sin[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"];
Print[N[Sqrt[a^2 + b^2], prec]]; Print[DateString[]];,
If[Mod[d, 4] == 2, f[x_] = x^(1/x); ClearAll[a, b, h];
a[n_] :=
Sum[StirlingS1[n, k]*
Sum[(-j)^(k - j)*Binomial[k, j], {j, 0, k}], {k, 1, n}];
a[0] = 1; g = 2 I/Pi - Sum[-I^(n + 1) a[n]/Pi^(n + 1), {n, 1, d}];
Print[DateString[]];
Print[T0 = SessionTime[]];
Print[N[
a = -Re[g] - (1/Pi)^(d)*
NIntegrate[
Simplify[Cos[Pi*x]*D[f[x], {x, d}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"];
Print[N[
b = Im[g] + (1/Pi)^(d + 1)*
NIntegrate[
Simplify[Cos[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"];
Print[N[Sqrt[a^2 + b^2], prec]]; Print[DateString[]];,
If[Mod[d, 4] == 3, f[x_] = x^(1/x); ClearAll[a, b, h];
h[n_] :=
Sum[StirlingS1[n, k]*
Sum[(-j)^(k - j)*Binomial[k, j], {j, 0, k}], {k, 1, n}];
h[0] = 1; g = 2 I/Pi - Sum[-I^(n + 1) h[n]/Pi^(n + 1), {n, 1, d}];
Print[DateString[]];
Print[T0 = SessionTime[]];
Print[
N[a = -Re[g] + (1/Pi)^(d + 1)*
NIntegrate[
Simplify[Cos[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"];
Print[
N[b = Im[g] - (1/Pi)^(d + 1)*
NIntegrate[
Simplify[Sin[Pi*x]*D[f[x], {x, d + 1}]], {x, 1, Infinity},
WorkingPrecision -> prec*(105/100),
PrecisionGoal -> prec*(105/100)], prec]];
Print[SessionTime[] - T0, " seconds"];
Print[N[Sqrt[a^2 + b^2], prec]]; Print[DateString[]];]]]]
Memory use:
"Thu 15 Mar 2018 16:30:46" .3 GB. Total used by programs 3.8 GB.
Here is a break down of the memory use as of 16:45 March 17, 2018
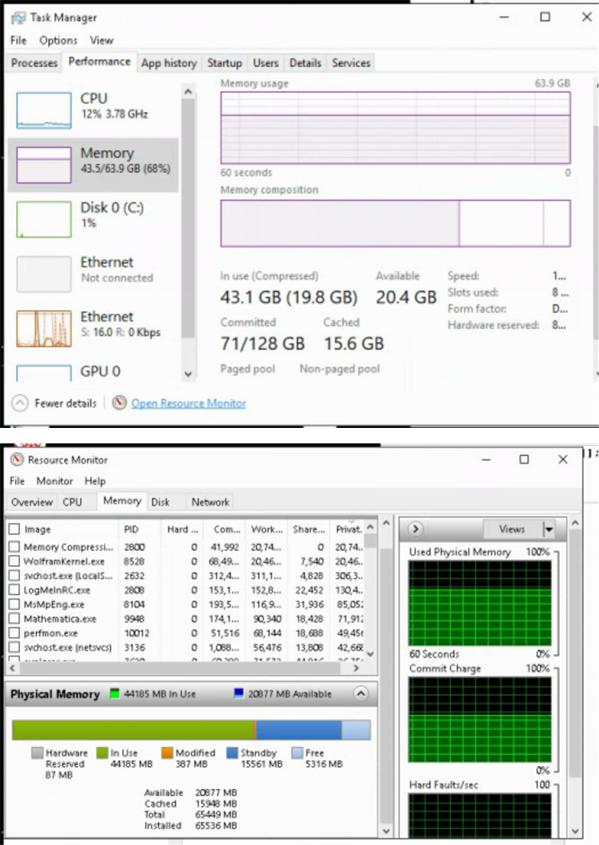
Mar 18, 2018, 8:10 AM
Just in case I run out of memory, I increased the size of my paging file!
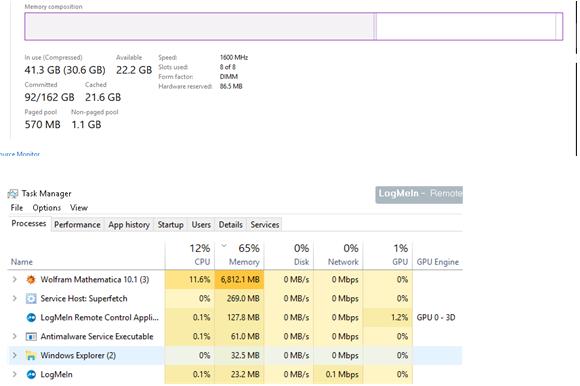
"Sun 17 Mar 2018 16:00:00" 15 GB. Total used by programs 49.92 GB.
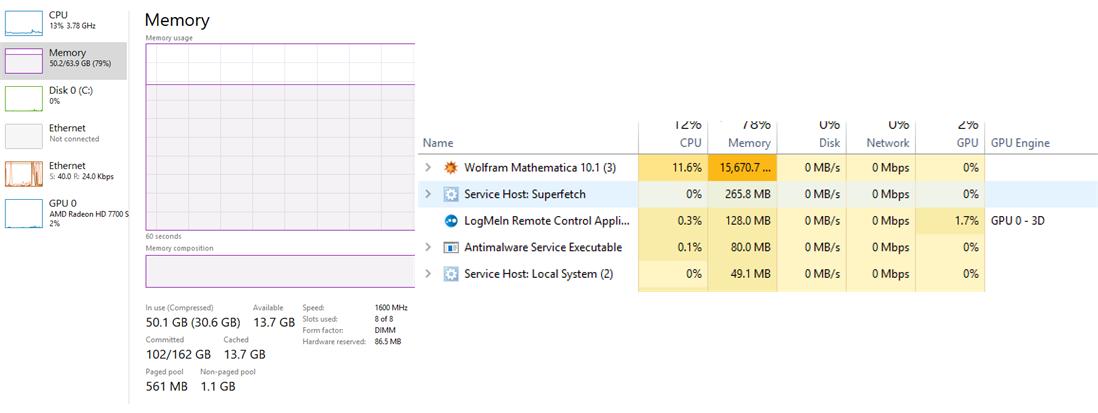

I no longer believe the V 11's use a lot more memory. If I hadn't increased my paging file Windows would have closed Mathematica already!

I might be slowing the computation down a little, but I don't want to take any chances of running out of memory, so I increased the paging file 1 more time. 
 The computer has been committing up to 160 GB of total RAM for a while now.
The computer has been committing up to 160 GB of total RAM for a while now.  Finally, the committed memory is going down.
Finally, the committed memory is going down. 
My computer is acting real sluggish right now. Mathematica is using a minimum amount of DDR3 RAM, but the computer is still committing a near-record of virtual RAM.  My computer is acting too funny, so I aborted the evaluation. The kernel remained running and overall memory remained maxed out. I tried to retrieve a and b (the variables with the real and imaginary parts of the solution), but the computer wouldn't recall them for me. The computer won't evaluate any Mathematica operations. I am restarting my computer and inspecting the damage!
My computer is acting too funny, so I aborted the evaluation. The kernel remained running and overall memory remained maxed out. I tried to retrieve a and b (the variables with the real and imaginary parts of the solution), but the computer wouldn't recall them for me. The computer won't evaluate any Mathematica operations. I am restarting my computer and inspecting the damage!
Update:
Windows said it found no errors on my hard drive; that's great!
I'm going to replace my Intel 6 core processor with a faster 8 -core Intel Xeon E5-2687W v2 CPU, and add an additional hard drive. The new processor and my motherboard both take 128 GB RAM, but ECC is the only 16G DDR3 mims I can find. I'm not sure if my MSI Big Bang-XPower II will take ECC. 40,000 digits of the integral analog might have to wait for me to get a new system. I am working on a new program to compute the MRB constant in little steps and will use it on my new processor.