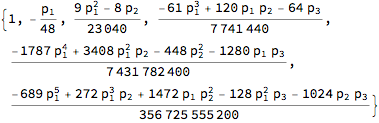You can weight the $c_i$ with an indeterminate t^i, and compute the series as a function of t:

genus[Q_, n_Integer] := 
  Module[{z, x}, 
   SymmetricReduction[
      SeriesCoefficient[
       Product[ComposeSeries[Series[Q[z], {z, 0, n}], 
         Series[x[i] z, {z, 0, n}]], {i, 1, n}], n], 
      Table[x[i], {i, 1, n}], 
      Table[Subscript[c, i] t^i, {i, 1, n}]][[1]] // FactorTerms];  (* <-- weights t^i *)
AgenusTotal[n_Integer] := 
  Total[Table[genus[(Sqrt[#]/2)/Sinh[Sqrt[#]/2] &, i] /. c -> p, {i, 0, n}]];
Series[Sqrt[AgenusTotal[3]], {t, 0, 5}]

You can also take the square root of the series:

Sqrt[Series[AgenusTotal[3], {t, 0, 5}]]

To get rid of the t, extract the coefficients; they can be added together with Total:

CoefficientList[Sqrt@Series[AgenusTotal[3], {t, 0, 5}], t] // Simplify