As Daniel Lichtblau stated, RandomVariate combined with a specific distribution (such as NormalDistribution) does the trick, and Mathematica provides plenty of built-in distributions to play with. One benefit of using built-in distributions is that we can easily and efficiently manipulate them symbolically.
For instance, numeric random variates of a specific distributions are available:
RandomVariate[NormalDistribution[0, 1], {20}]
(* {0.270132, -1.79075, 0.0748062, 0.715661, 0.617855, 0.202395, \
-1.01686, -0.125683, 1.5585, 1.42078, 2.04629, -0.309086, -1.33024, \
0.591959, 0.530648, -0.52868, -1.07803, 0.504637, 0.327951, -0.569275} *)
Variance[%]
(* 0.963508 *)
... but also, it is possible compare this with symbolic result:
Variance[NormalDistribution[0, 1]]
(* 1 *)
EDIT: This is probably closest to what you want. This is an example directly from Mathematica documentation:
dist = ProbabilityDistribution[(Sqrt[2] / Pi) (1 / (1 + x^4)), {x, -Infinity, Infinity}];
It's important to define the function so that it integrates to unity over range of defined ProbabilityDistribution.
Integrate[(Sqrt[2] / Pi) (1 / (1 + x^4)), {x, -Infinity, Infinity}]
(* 1 *)
Some random variates:
Histogram[RandomVariate[dist, {1000}]]
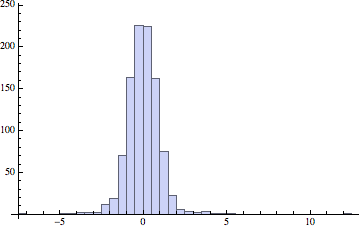
And symbolic manipulation is possible:
Variance[dist]
(* 1 *)
Also, using TransformedDistribution, we can also map one distribution to another. Let's take inverse function of cumulative distribution function of a normal distribution:
InverseFunction[CDF[NormalDistribution[0, 1]]][x]
(* -Sqrt[2] InverseErfc[2 x] *)
Now we use this to map uniform distribution to above normal distribution:
dist = TransformedDistribution[-Sqrt[2] InverseErfc[2 x], x \[Distributed] UniformDistribution[{0, 1}]];
We can generate transformed numeric random variates this way:
Histogram[RandomVariate[dist, {10000}]]
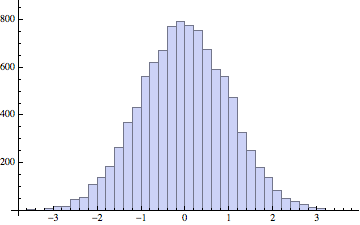
Also, symbolic manipulation is still possible. Now it's considerably slower, though (first value is runtime in seconds, second is the symbolic result):
Variance[dist] // AbsoluteTiming
(* {2.605953, 1} *)