A common function to 'unwrap' a list of data which has had a modulus operation working on it is still absent from the Wolfram Language. This also quite commonly happens when you measure something in the lab which is for example an angle that jumps back to '0' after every rotation. To solve this, I wrote my own function, hopefully this is helpful for you. Here it is:

ClearAll[Unwrap]
Unwrap[lst_List]:=Unwrap[lst,2Pi] (* phase jumps of 2Pi is the default because of trigonometric funtions *)
Unwrap[lst_List,\[CapitalDelta]_]:=Unwrap[lst,\[CapitalDelta],Scaled[0.5]] (* default tolerance is half the phase jump \[CapitalDelta] *)
Unwrap[lst_List,\[CapitalDelta]_,tolerance_]:=Module[{tol,jumps},
    tol=If[Head[tolerance]===Scaled,
        \[CapitalDelta] tolerance[[1]]
    ,
        tolerance
    ];
    jumps=Differences[lst];
    jumps=-Sign[jumps]Unitize[Chop[Abs[jumps],tol]];
    jumps=\[CapitalDelta] Prepend[Accumulate[jumps],0];
    jumps+lst
]

When a list is given, the default period is assumed to be 2Pi, and the tolerance Pi. But one can specify any one likes with the second and third arguments.

So let's create some data and plot it:

dat=Table[Sin[0.2x]+4Sin[0.05x],{x,0,200}];
ListPlot[dat,AspectRatio->1/4,ImageSize->600,PlotMarkers->Automatic]

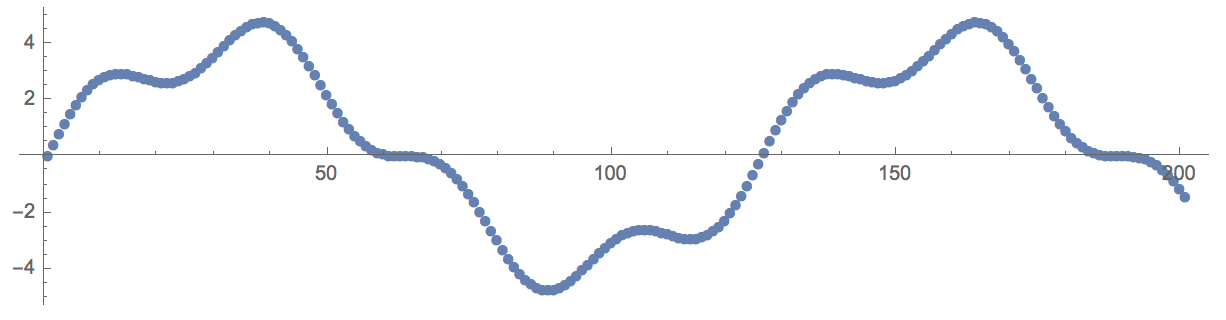
Now, let's take the modulus of the data and plot it:

mod=Mod[dat,4,-2];
ListPlot[mod,AspectRatio->1/4,ImageSize->600,PlotMarkers->Automatic]

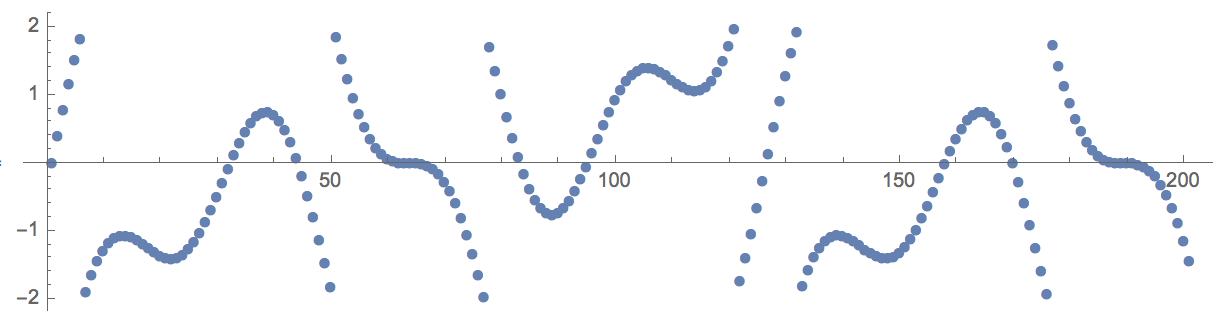
Now we indeed have many sharp jumps, but with the above function we can undo this:

unmod=Unwrap[mod,4];
ListPlot[unmod,AspectRatio->1/4,ImageSize->600,PlotMarkers->Automatic]

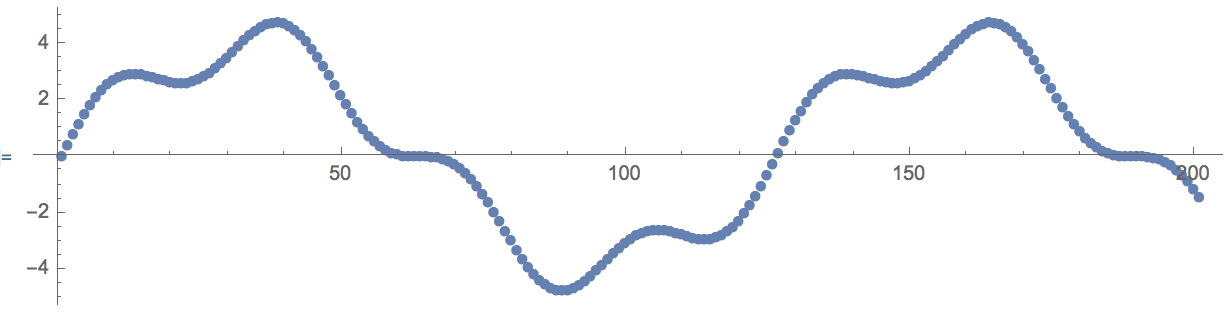
So we return now to our original data; great!

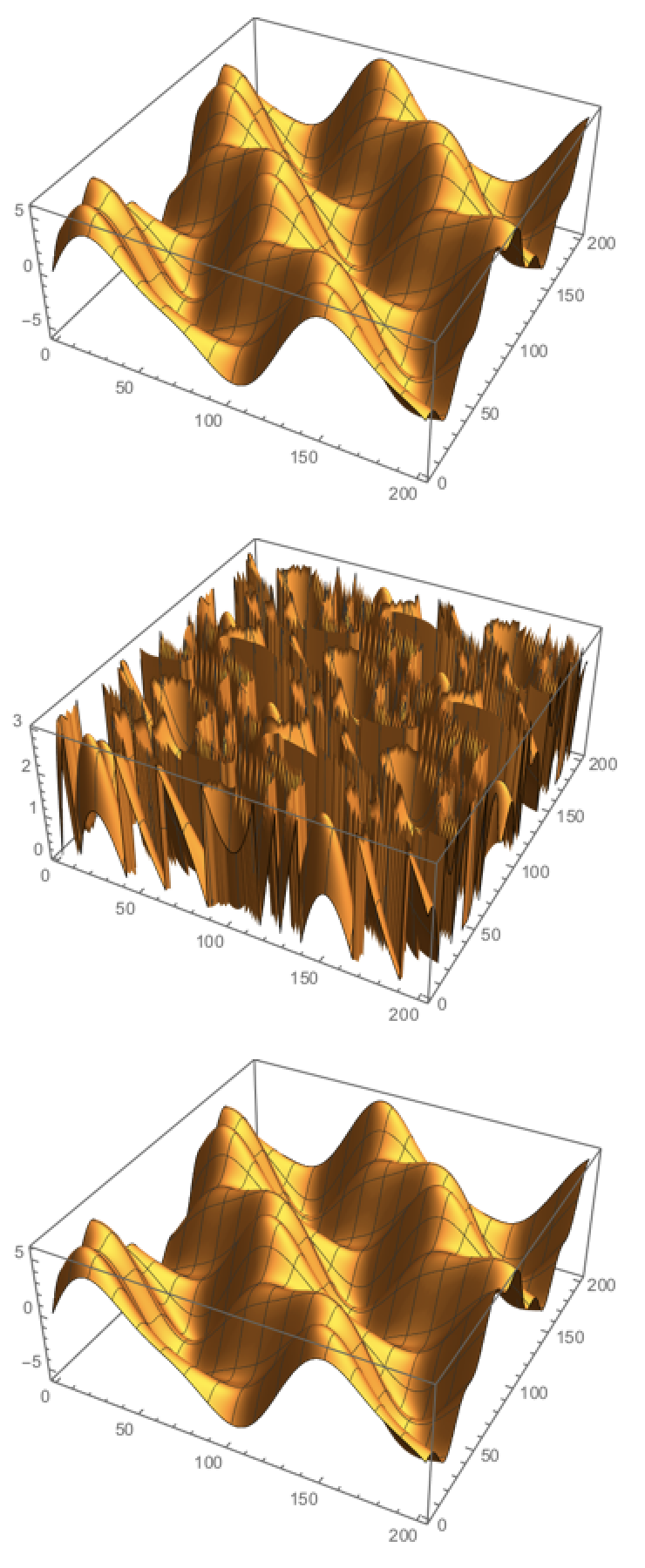
With some tricks we can also do it with 2D-data, here i create some data, plot it, mod it (what a mess!), plot it, unmod it, plot it:

dat=Table[Sin[0.2x]+4Sin[0.05x+0.05y]+Sin[0.1y],{x,0,200},{y,0,200}];
ListPlot3D[dat]
mod=Mod[dat,3];
ListPlot3D[mod]
unmod=Unwrap[#,3]&/@mod;
tmp=Unwrap[#,3]-#&[unmod[[All,1]]];
unmod=unmod+tmp;
ListPlot3D[unmod]

Hope you enjoy it and find it useful!