The rule is simple:
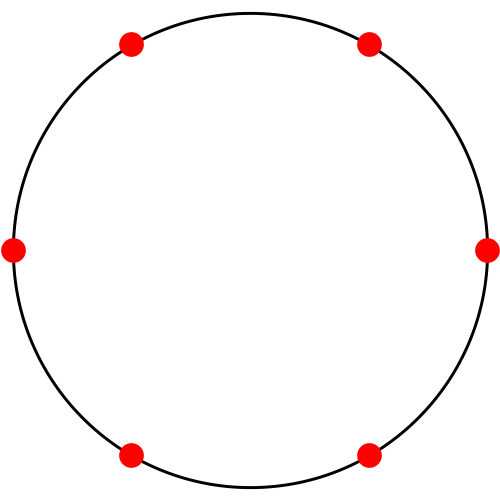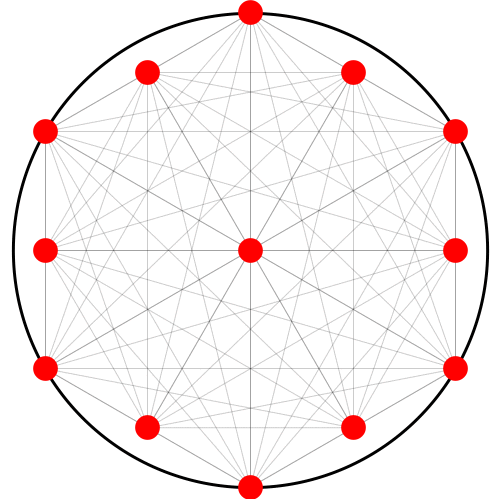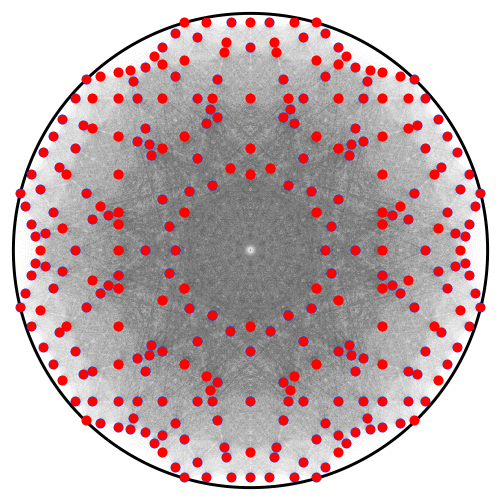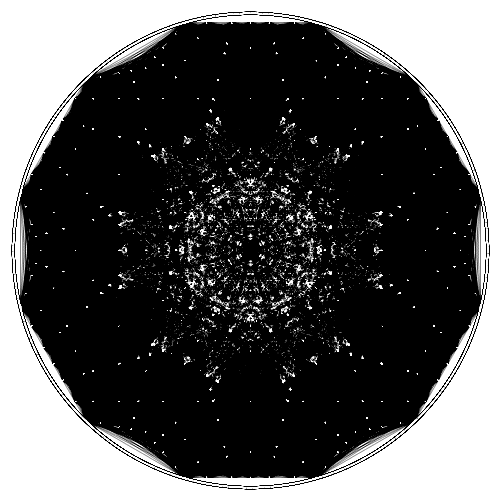
- Start with n-points in any arbitrary configuration.
- Connect every point to every other point with a line.
- Draw a point where any new intersections occur.
- These intersections become your initial set of points for the next iteration. Repeat the process.
I only took it 3 iterations because render time blows up, but it looks like it approaches a particular figure as # of iterations -> infinity. We may suspect that different sets of initial points yield a converging image, while others do not converge. Much like a geometric series.
Here is a closer look at the 3rd iteration:

We could also keep the points from previous iterations, yielding something more like this:
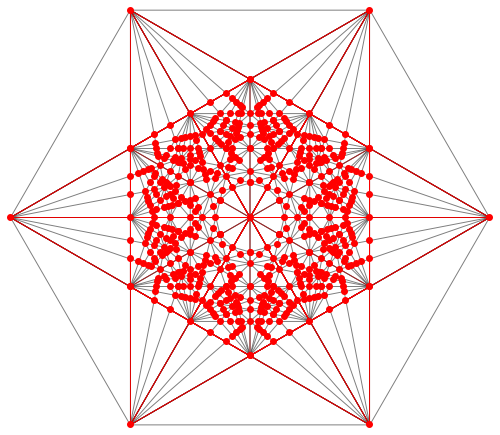
The code is not super clean, did a lot of manual stuff.
pts0 = N[CirclePoints[6]];
lines = Subsets[pts2, {2}];
threshold = 0.0000000001;
lul = {};
Monitor[
Do[
p = Quiet[
Position[lul,
t_ /; (RegionDistance[InfiniteLine[lines[[i]]], t[[1]]] <
threshold &&
RegionDistance[InfiniteLine[lines[[i]]], t[[2]]] <
threshold)]];
Quiet[If[MatchQ[p, {}],
AppendTo[lul, lines[[i]]],
Set[lul,
ReplacePart[lul,
p[[1]][[1]] ->
Flatten[MaximalBy[{lines[[i]], lul[[p[[1]][[1]]]]},
EuclideanDistance[#[[1]], #[[2]]] &, 1], 1]]]]]
Clear[p];
, {i, 1, Length[lines]}]
, {i, Length[lul]}]
longestUniqueLines=lul;
intersectionpoints =
Monitor[
DeleteDuplicates[
Flatten[
Table[
If[MatchQ[
RegionIntersection[Line[longestUniqueLines[[i]]],
Line[longestUniqueLines[[
j]]]], _EmptyRegion] \[Or] (RegionDistance[
Line[longestUniqueLines[[i]]],
longestUniqueLines[[j]][[1]]] < threshold) \[Or]
(RegionDistance[Line[longestUniqueLines[[i]]],
longestUniqueLines[[j]][[2]]] < threshold) \[Or]
(RegionDistance[Line[longestUniqueLines[[j]]],
longestUniqueLines[[i]][[1]]] < threshold) \[Or]
(RegionDistance[Line[longestUniqueLines[[j]]],
longestUniqueLines[[i]][[2]]] < threshold)
, Nothing,
Flatten[RegionIntersection[Line[longestUniqueLines[[i]]],
Line[longestUniqueLines[[j]]]][[1]]]
], {i, Length[longestUniqueLines]}, {j,
Delete[Range[Length[longestUniqueLines]],
Table[{q}, {q, i}]]}]
, 1]
, Abs[#1[[1]] - #2[[1]]] < threshold \[And]
Abs[#1[[2]] - #2[[2]]] < threshold &];
, {i, j}]