Run this

Clear[into1, pureIntonationTree]
into1[l_List] := Block[{l0 = NestWhile[(1/2) # &, #, # > 2 &] & /@ l},
   Union[If[MemberQ[l0, 2], Join[{1}, l0], l0]]
   ] /; VectorQ[l, (# >= 1) &]
pureIntonationTree[] := 
 Module[{s0 = {1 (* c *) , (9/8) (* d *), (10/9) (* ,e *), (16/15) (* 
     f *), (9/8) (* g *), (10/9) (* ,a *), (9/8) (* ,h *), (16/15) (* 
     c *)}, s1, s2, \[Delta] = 1/43, h = 2^(1/12)},
  s1 = into1 /@ 
    NestList[FoldList[Times, #[[5]], Rest[s0]] &, 
     FoldList[Times, First[s0], Rest[s0]], 12];
  s2 = ConstantArray @@@ 
    Transpose[{Range[Length[s1] - 1, 0, -1], Length /@ s1}];
  Graphics[{Blue, PointSize[\[Delta]/2], 
    Point[Transpose[#]] & /@ Inner[List, s1, s2, List],
     {White, Opacity[0.1], EdgeForm[Black], 
     Polygon[{{1 - \[Delta], 
        13}, {1 - \[Delta], -1}, {h - \[Delta], -1}, {h - \[Delta], 
        13}, {1 - \[Delta], 13}}]},
    {Gray, Opacity[0.6], EdgeForm[Black], 
     Polygon[{{h - \[Delta], 
        13}, {h - \[Delta], -1}, {h^2 - \[Delta], -1}, {h^2 - \
\[Delta], 13}, {h - \[Delta], 13}}]},
    {White, Opacity[0.1], EdgeForm[Black], 
     Polygon[{{h^2 - \[Delta], 
        13}, {h^2 - \[Delta], -1}, {h^3 - \[Delta], -1}, {h^3 - \
\[Delta], 13}, {h^2 - \[Delta], 13}}]},
    {Gray, Opacity[0.6], EdgeForm[Black], 
     Polygon[{{h^3 - \[Delta], 
        13}, {h^3 - \[Delta], -1}, {h^4 - \[Delta], -1}, {h^4 - \
\[Delta], 13}, {h^3 - \[Delta], 13}}]},
    {White, Opacity[0.1], EdgeForm[Black], 
     Polygon[{{h^4 - \[Delta], 
        13}, {h^4 - \[Delta], -1}, {h^5 - \[Delta], -1}, {h^5 - \
\[Delta], 13}, {h^4 - \[Delta], 13}}]},
    {White, Opacity[0.1], EdgeForm[Black], 
     Polygon[{{h^5 - \[Delta], 
        13}, {h^5 - \[Delta], -1}, {h^6 - \[Delta], -1}, {h^6 - \
\[Delta], 13}, {h^5 - \[Delta], 13}}]},
    {Gray, Opacity[0.6], EdgeForm[Black], 
     Polygon[{{h^6 - \[Delta], 
        13}, {h^6 - \[Delta], -1}, {h^7 - \[Delta], -1}, {h^7 - \
\[Delta], 13}, {h^6 - \[Delta], 13}}]},
    {White, Opacity[0.1], EdgeForm[Black], 
     Polygon[{{h^7 - \[Delta], 
        13}, {h^7 - \[Delta], -1}, {h^8 - \[Delta], -1}, {h^8 - \
\[Delta], 13}, {h^7 - \[Delta], 13}}]},
    {Gray, Opacity[0.6], EdgeForm[Black], 
     Polygon[{{h^8 - \[Delta], 
        13}, {h^8 - \[Delta], -1}, {h^9 - \[Delta], -1}, {h^9 - \
\[Delta], 13}, {h^8 - \[Delta], 13}}]},
    {White, Opacity[0.1], EdgeForm[Black], 
     Polygon[{{h^9 - \[Delta], 
        13}, {h^9 - \[Delta], -1}, {h^10 - \[Delta], -1}, {h^10 - \
\[Delta], 13}, {h^9 - \[Delta], 13}}]},
    {Gray, Opacity[0.6], EdgeForm[Black], 
     Polygon[{{h^10 - \[Delta], 
        13}, {h^10 - \[Delta], -1}, {h^11 - \[Delta], -1}, {h^11 - \
\[Delta], 13}, {h^10 - \[Delta], 13}}]},
    {White, Opacity[0.1], EdgeForm[Black], 
     Polygon[{{h^11 - \[Delta], 
        13}, {h^11 - \[Delta], -1}, {h^12 - \[Delta], -1}, {h^12 - \
\[Delta], 13}, {h^11 - \[Delta], 13}}]},
    {White, Opacity[0.1], EdgeForm[Black], 
     Polygon[{{h^12 - \[Delta], 
        13}, {h^12 - \[Delta], -1}, {h^13 - \[Delta], -1}, {h^13 - \
\[Delta], 13}, {h^12 - \[Delta], 13}}]}
    }, AspectRatio -> 1/2,
   Frame -> True,
   FrameLabel -> {None, None, "Tasten", "Tonarten"},
   FrameTicks -> {{{{12, "C"}, {11, "G"}, {10, "D"}, {9, "A"}, {8, 
        "E"}, {7, "H"}, {6, "Fis"}, {5, "Des"}, {4, "As"}, {3, 
        "Es"}, {2, "B"}, {1, "F"}, {0, "C"}}, 
      None}, {{{1, "c"}, {h^2, "d"}, {h^4, "e"}, {h^5, "f"}, {h^7, 
        "g"}, {h^9, "a"}, {h^11, "h"}, {h^12, "c"}}, None}}
   ]
  ]

to see how many different frequencies of the pure intonation are bundled onto one key on a keyboard

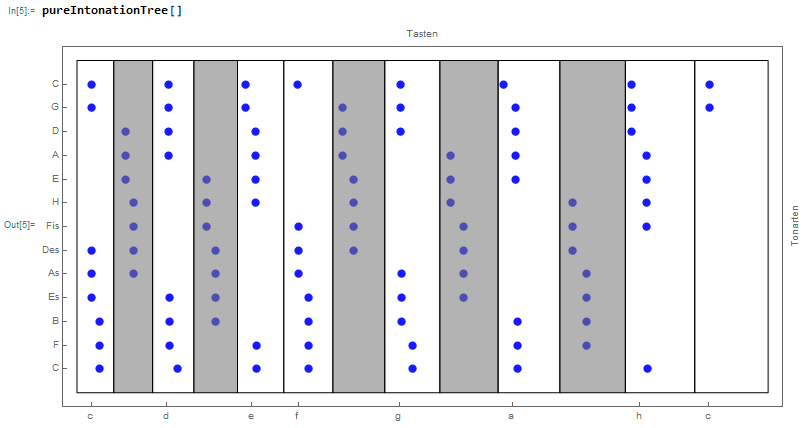
Observe how the C from the end of the cycle of fifths (12 fifths or 7 octaves) shifts with respect to the starting C. Observe also how the frequencies mapped to the same key on the keyboard deviate from each other less than they deviate from the nearest frequency of a neighboring key. So it justifies the equal intonation beside the fact that one can -impure- modulate to anywhere.