Introduction
The goal of my project during the Wolfram Summer School 2018 was to develop a genetic algorithm framework that can handle a variety of different data structures. Genetic algorithms use methods inspired by evolution like mutation and crossover to solve problems that are hard to tackle algorithmically. These methods are extensively used in many fields of science and technology and can come up with solutions that engineers never have thought about e.g. Nasa's evolved antenna. Genetic algorithms generate successive generations of a population by applying the evolutionary operators i.e. selection, mutation and crossover. The role of selection is to guarantee that better individuals have a higher chance to create offsprings in the next generation. During the selection mechanism a fitness function is used that quantifies how well a given element performs on the problem to be solved.
The Framework
My purpose was to create a high-level framework that requires minimal code from the user to set up and run a genetic algorithm with custom data types. The new function takes the following parameters:
GeneticAlgorithm[Init, Fitness, ConstraintList, Crossover, Mutation]
Parameters:
- Init: The initial element of the population that specifies the type of the objects the function has to work with.
- Fitness: The fitness function takes an element of the population and outputs its fitness value that quantifies how well the element is performing on the problem at hand.
- ConstraintList (Optional): A list of constraints can be provided that don't let a certain set of elements appear in the population.
- Crossover and Mutation (Optional): These functions describe how the elements of the population are supposed to be changed. The framework can automatically handle some standard data types, but for custom object types these functions need to be specified.
Specifying these functions and getting the GeneticAlgorithm function run is typically just a few lines of code in Mathematica.
Fitness Landscape
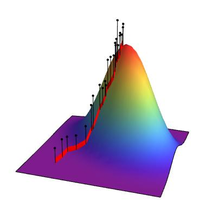
The space of possible solutions can be described with a fitness landscape where each solution is assigned its fitness value. The goal of the genetic algorithm is to find the global maxima in this landscape which can be a challenging task when working with a complicated fitness function. The fitness landscape is typically a multidimensional surface, but in the following example the elements of the population are represented as two dimensional vectors so our fitness landscape becomes three dimensional. The simulation shows how the population evolves until reaching the global maxima.
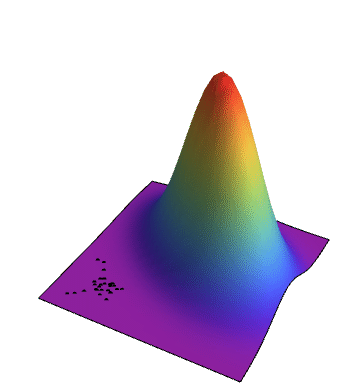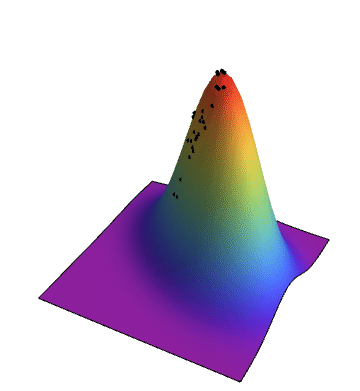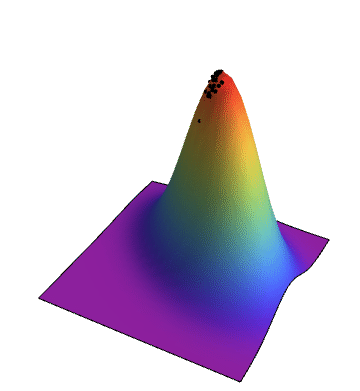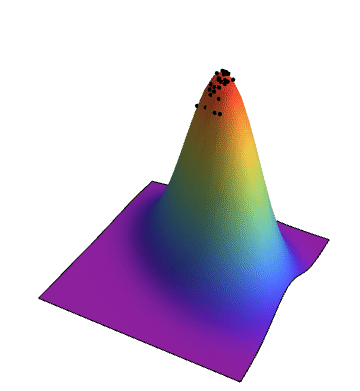
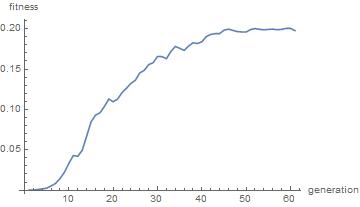
The plot below shows how the average fitness of the population increases from generation to generation:
Use Cases
To demonstrate the power and universality of genetic algorithms I created some use cases taken from different domains where the use of these evolutionary methods can really make a difference in solving tough problems.
Fitting Ellipses Inside a Random Polygon
It is a hard problem to find the best fitting ellipse inside a random polygon as no analytical solution exists. However, genetic algorithms can easily tackle such a problem. The image on the left shows an element of the initial population while the image on the right shows a typical element just after a few generations which shows that the population converges reasonably fast to the best solution.


Balancing Binary Trees
Another use case I created to show the usefulness of genetic algorithms is balancing binary trees. In such binary trees the nodes are organized in a very strict manner having bigger and smaller elements in different branches at each node. So the order in which the numbers are added to the binary tree determines the structure of the resulting tree. That's why a binary tree is represented as an ordered list of numbers where the mutation and crossover operations are interpreted in terms of permutations that change the order of elements in the list. The two figures below show how the population evolves in only 20 generations to come up with an almost perfectly balanced tree.
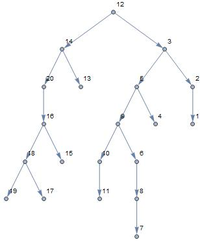
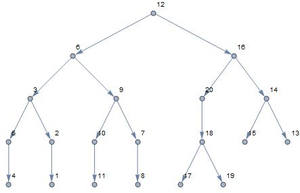
Evolution of Programs
The branch of computer science that deals with evolving computer code is called genetic programming and its methods can provide solutions that compete or sometimes even outperform human-engineered results. The crucial question is which representation of programs allows greatest flexibility when performing the genetic operations i.e. selection, crossover and mutation. The way I choose to represent programs is by creating a derivation graph based on a certain grammar of the programming language. This grammar is the Backus Naur Form that enumerates all the valid syntactical constructs of the language. A simple grammar I created for polynomials is the following:
rulesPolynom = {
root :> Hold[Function[x, expr]],
expr :> Hold[expr + expr],
expr :> Hold[exprX * exprX],
expr :> Hold[exprX],
exprX :> const Hold[x]^const,
const :> RandomInteger[{-10, 10}]
};
Every program can be represented as a derivation tree that specifies in what order the certain derivation rules are used. An example can be seen below:
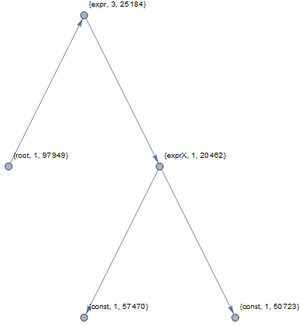
${Function}$[ ${x}$, ${2 x^3}$]
Each node consists of tree entities in the derivation graph: the name of the current symbol, the number of the derivation rule that we apply for the given symbol and finally a random number to keep the nodes unique.
The advantage of using such a derivation graph as a representation of programs is that it makes it easy to perform the mutation and crossover mechanisms on the programs. When mutating a certain code a random node in its derivation graph is picked and replaced by a newly generated random derivation started from the given symbol. Performing the crossover of two programs is just as convenient: a common node is chosen in the two graphs (not taking into account the random number that makes the nodes unique) and the two branches of the different graphs are then swapped to create an offspring for the next generation. These operations always result in syntactically valid and perfectly functional programs.
For this example the fitness function simply measured how well the given program approximates a certain target function. During this evolution a large variety of different programs occurred ranging from quite simple to extremely complicated ones.

${Function}$[ ${x}$, ${\frac{4}{x^2}-\frac{4}{x^3}}$]
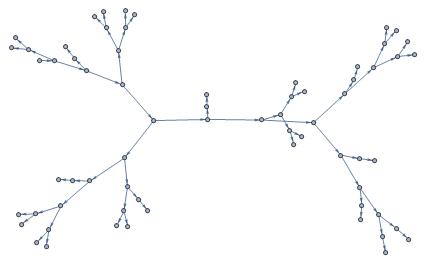
${Function}$[ ${x}$, ${-\frac{4}{x^6}-5 x^5-\frac{2}{x^5}+20 x^4+9 x^3+\frac{20}{x^3}+12 x^2-\frac{4}{x^2}-5 x-\frac{12}{x}+2}$]
The above-described example works with a simple grammar covering functions made of polynomials. However, the BNF grammar can be created to work with any set of Wolfram Language functions. It is also possible to create a grammar that describes the whole Wolfram Language allowing programs to evolve into any form possible. At first glance, it seems like an elaborate task to create this complete grammar, but I think it can be achieved by simply scraping the documentation as standard notations are used to describe the usage of functions e.g. f , expr, crit.
Discussion and Future Directions
This genetic algorithm framework can be used for arbitrary objects by specifying the mutation and crossover functions that are only a few lines of Wolfram Language code for a typical application. The effectiveness of the GeneticAlgorithm function can be further improved by introducing some advanced methods to maintain the diversity of the population. Also, different types of problems might work best with different settings of the hyperparameters (e.g. size of population) and selection mechanisms. For this reason, a meta-algorithm could be developed that would set these simulation parameters based on the analysis of the problem before actually running the genetic algorithm making this effective optimization technique even more efficient.
To check out the code please follow this Github link.