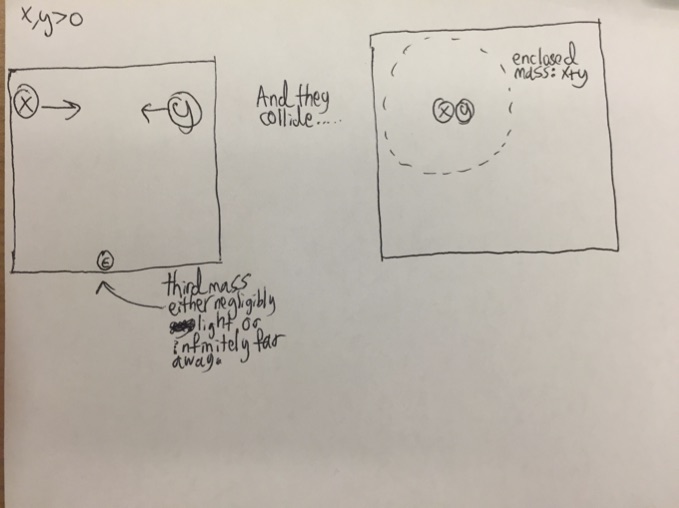
It has been hypothesized that the (Newtonian) three-body problem is computationally universal (or Turing complete). This means (roughly speaking) that any computer program can be transformed into a three-body problem initial condition which after being simulated can eventually be decoded as the output of the initial computer program. My task was to find ways to encode basic computer programs (in particular, addition and multiplication) in terms of three-body problem initial conditions.

For example, addition (of two positive real numbers) may (under some assumptions about what can be done with the third mass) be expressed in terms of the three-body problem in the following way:

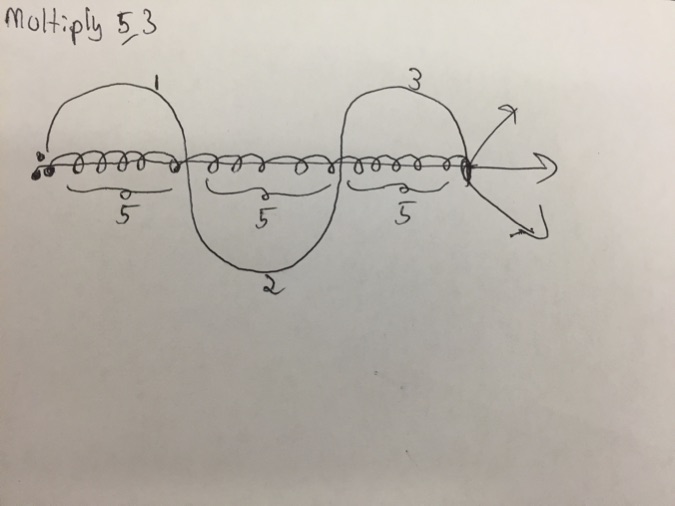
I then attempted to find initial conditions that could encode the multiplication of two positive numbers. I searched for initial conditions which produced trajectories of the following form:

What I attempted to do was to take the initial condition:

{1 -> Association["Mass" -> 1, "Position" -> {0, 0}, 
     "Velocity" -> {0, 0}], 
   2 -> Association["Mass" -> 1, "Position" -> {0, -.9}, 
     "Velocity" -> {1, 0}], 
   3 -> Association["Mass" -> 1, "Position" -> {0, .9}, 
     "Velocity" -> {-2, 0}*0.8]};

whose trajectory looks like:

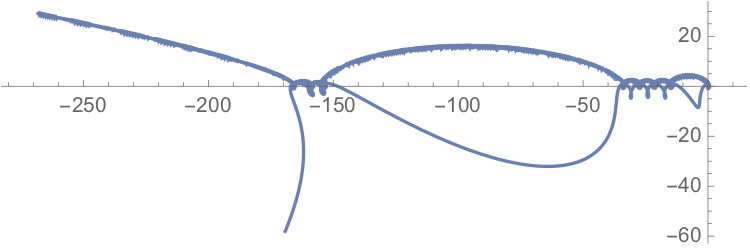
and then perturb it repeatedly, on each iteration choosing the initial condition that produces a trajectory whose form is closest to the desired form.

https://github.com/watcher00090/Summer2018Starter/tree/master/Project

On another note, my mentor (Vladimir Grankovsky) wrote code to compute how long it takes for a given solution to the three-body problem to become trivial (the system is called "trivial" if one particle is flying away from the other two and has a very low probability of returning) and then produced a plot of the time it takes for the solution to become trivial against the velocity of the second particle (vel2) with respect to the initial conditions:

{m1, m2, m3, pos1, pos2, pos3, vel1, vel3} = {1., 1., 1., {-1.0, 0.}, {0.0, 0.0}, {1.0, 0.0}, {.5, .5}, {0, 0`}}

where the x-coordinate of vel2 varies from -0.01 to 0.01 and y-coordinate of vel2 varies from -0.01 to 0.02 (both varying with a step size of 0.01/160):