Augmented and Virtual reality functions in Mathematica

Overture

The goal of my project at Wolfram Summer School '18 was to implement VR and AR visualization features in the Wolfram Language. Conceptually, the underlying idea was to create two simple functions through which deploy in a VR or AR environment any 3D object created from Mathematica, spanning from a random solid (e.g. created using the ConvexHullMesh function):

ConvexHullMesh[RandomReal[5, {50, 3}]]

to a detailed view of 3D elevation data for a specific region:

ListPlot3D[GeoElevationData[GeoDisk[Entity["City", {"Tivoli", "Lazio", "Italy"}], 4 Quantity[1, "Kilometers"]], GeoZoomLevel -> 12]]

How

The two functions ARDeploy and VRDeploy work in conjunction with the WebVR BoilerPlate platform and AR.js library, which provide the required JavaScript tools to manage the VR/AR environments. The objects representation is translated from Mathematica into a js compatible format by Three.js and Aframe.js libraries. In particular, VRDeploy enables to investigate abstract mathematical (and any 3D Mathematica models) representations in a new environment leading to a clearer and easier understanding of them. In combination with mobile devices, equipped with a headset, enables the user full immersion experience. ARDeploy, on the other side, enables the "on-screen" exploration of the same objects compatible in VRDeploy, attaching it to a marker which could be visualized in the Mathematica notebook. The great difference between the two functions relies on the way the 3D object is explored. The VRDeploy offers a static full immersive point of view while ARDeploy offers a dynamic exploration.

These two functions (in form of Mathematica package) and all the required files can be downloaded at https://github.com/DomenicoRomano/ARVRDeploy.

VRDeploy Example Code

VRDeploy (as ARDeploy) works with any 3D surfaces from Plot3D or Example Data. In the example code below the 3D surface from Plot3D is translated in a VR object, VRDeploy returns a link to a webpage in which there is the WebVR environment with the Plot3D object visualised:

VRDeploy[Plot3D[0.5 *Sin[0.4*x y], {x, -4, 4}, {y, -4, 4}, MaxRecursion -> 4]]

Below a screenshot view of the webpage returned by VRDeploy as seen from mobile devices, this provides the full immersion experience. It is also possible to switch to normal view and then navigate the VR scene using the mobile device orientation hardware.

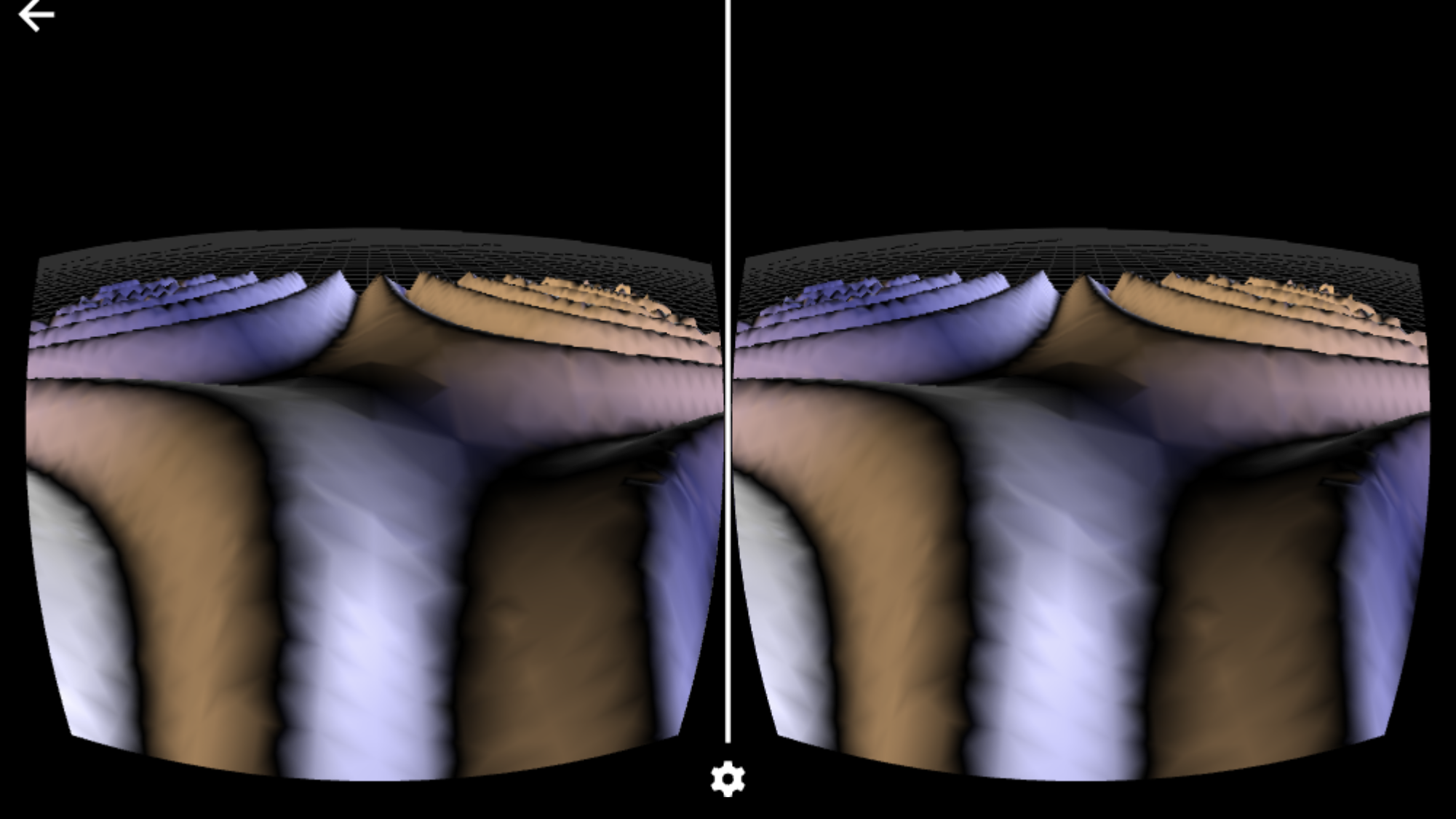
Below a view of the same webpage as above returned by VRDeploy as seen from a laptop/desktop computer:

Another example is the VR visualization of the stars distribution around the Earth, using the StarData function. The following code extracts the position of the 35000 closest stars to our Sun, then converts the distances to parsec and VRDeploy them:

VRDeploy[Graphics3D[
  Sphere[QuantityMagnitude[
    DeleteMissing[StarData[EntityClass["Star", 
     List[Rule[EntityProperty["Star", "DistanceFromEarth"], 
       TakeSmallest[35000]]]], "HelioCoordinates"]]/3.26],
   .05], {
  Axes -> {True, True, True}, 
   AxesLabel -> {"pc", "pc", "pc"}, ImageSize -> Large}]]

Resulting in the picture below:

ARDeploy example

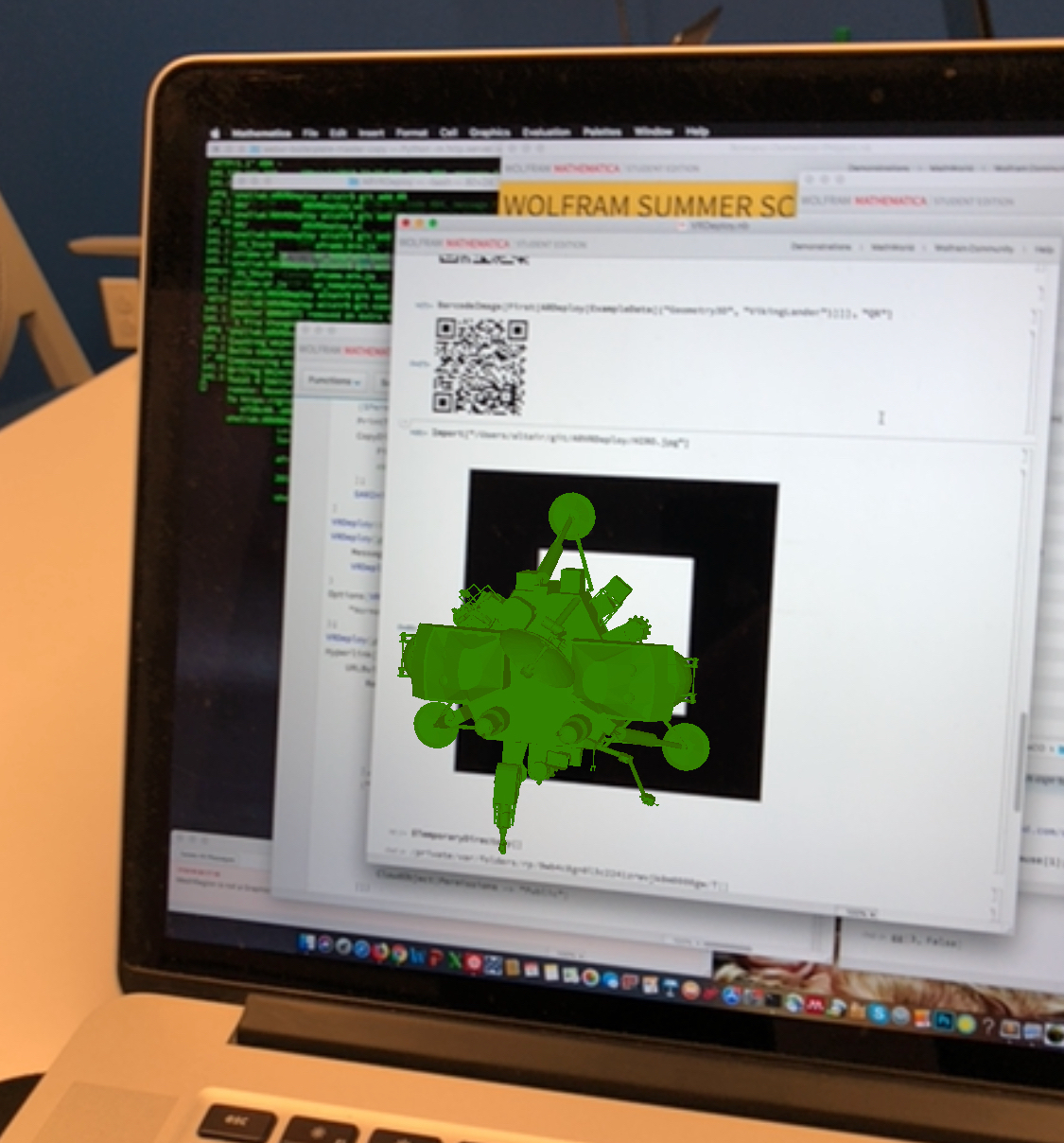
A simple example of ARDeploy function presented here use the Viking Lander model from the 3D Example data of Wolfram Mathematica, following is the code:

ARDeploy[ExampleData[{"Geometry3D", "VikingLander"}]]

The returned CloudObject is a link to a webpage, which can be easily converted to a QR code and scanned by mobile devices.

BarcodeImage[
 First[ARDeploy[ExampleData[{"Geometry3D", "VikingLander"}]]], "QR"]

The webpage opened in the mobile device will ask "to allow the application to access the camera". After granting the access to the camera the mobile device will recognize the marker, plotting on it the ARDeployed object:

Future Directions

Next steps require to enrich the visualization experience with interactive capabilities, displaying specific information or changing the object properties. Another required step is the marker independent placement of the object, using absolute GPS coordinates. The required mobile hardware improvements will be soon available. It will be also interesting to offer a virtual reality Mathematica notebook in which the user could experience the advantages to learn in a full-immersive three-dimensional virtual world.