Goal of the project
Analyse and study algorithms for tiling a prescribed region or the entire (euclidean) plane using zero or more copies of polyominoes from a given set of polyominoes.
What are polyominoes?
A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. A monomino would simply be a square, a domino is a rectangle made using two squares, a tromino would be a set of two arrangements of three squares - an L shaped and I shaped. In general, an n-omino is a set of n rook wise connected unit squares. The interesting thing about these arrangements is that there doesn't exist any formula for enumerating polyominoes of a given size, except for special cases.
Representation of a tile
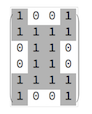
All the tiles are represented as a matrix filled with 1s and 0s representing occupied and unoccupied squares respectively.
The variable tiles is initialised to contain the following tiles: { 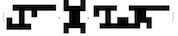 }
}
Representation of the surface to be tilled
Surface to be tilled is also a matrix (universe), initialised as a 50 x 50 zero matrix.
Initialising matrices
universe = Table[0, {50}, {50}]; visualUniverse = Table[0, {50}, {50}];
tiles = {{{0, 1, 1, 1, 1, 1, 1, 1}, {0, 0, 1, 0, 1, 0, 0, 0}, {1, 0, 1, 0, 0, 0, 0, 0}, {1, 1, 1, 1, 0, 0, 0, 0}}, {{1, 0, 0, 1}, {1, 1, 1, 1}, {0, 1, 1, 0}, {0, 1, 1, 0}, {1, 1, 1, 1}, {1, 0, 0, 1}}, {{1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1}, {1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0}, {0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0}, {0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0}}}
Reflections and rotations of the tiles
A function allTiles[tile] was made to produce all the unique reflections and rotations of a given tile.
tiles = Flatten[allTiles /@ tiles, 1];
ArrayPlot /@ tiles

Starting the tiling
A couple of tiles are added in the left top corner in universe (using the function addTile[tile, universe, {x,y}]. This is required so that the function growUniverse[universe, tiles, visualUniverse] has a region around which it can tile:
universe = addTile[tiles[[1]], universe, {1, 1}];
universe = addTile[tiles[[13]], universe, {1, 2}];
universe = addTile[tiles[[9]], universe, {7, 3}];

(The plot is actually of visualUniverse and not universe, which has different values for different tiles, just like universe - one has to add tiles to visualUniverse initially)
Expanding the tiling
Once there are a couple of tiles (perhaps in the top left corner), the growUniverse[universe, tiles, visualUniverse] can be used to add another tile around the perimeter in an optimum manner (based on a score function defined later in the post). 
Comparing arrangements
While expanding the tilled region along the boundary, a comparison has to be made between the various tilings produced after placing (a) tile around the perimeter in different ways. One easy way could be to see the area of the spanning rectangle produced and then choose the arrangement which gives least area. Unfortunately there are cases, like the one shown in right, which have same area but one leads to successful tiling while the other one doesn't.
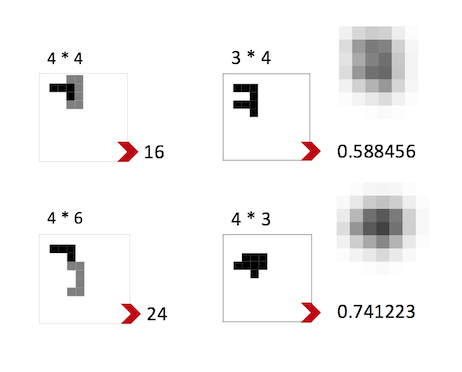
So, in order to compare - the image of the tiling is blurred and then maximum values of the image data are taken into consideration.
Scanning along the perimeter
The search region slides along the perimeter and calculates score for each best configuration produced while sliding, and then the configuration with maximum score is chosen.

The following image shows the sliding window (red) which slides along line produced by findPerimeter[universe]. The image adjacent to it shows the cost of adding the black tile to the positions in the sliding window (not all points in sliding window are checked). Lighter region represents less cost.

Detecting overlap
Overlap is detected by adding the positioned tile and universe and then checking the maximum value of the cells in the matrix.
Detecting Voids

ArrayPlot[universe]
img = Image[universe,"Bit"]
fImg=FillingTransform[Image[universe,"Bit"],Padding->0,CornerNeighbors->True]
Subtract[fImg,img]
Voids are detected by making use of FillingTransform which gives a version of image with all extended minima filled. The output of filling transform is compared with the original image.
Tilings produced



One can go on tiling indefinitely but the function needs some more optimisation to run faster.
Some functions for intuition
allTiles[tile_] := Module[{list = {}},
list = Join[NestList[rotatec, tile, 3],
NestList[rotatec, mirrorv[tile], 3]];
DeleteDuplicates[list]
]
Finds all the (unique) reflected and rotated tile configurations (almost 8) of the given tile.
positionTile[tile_, {x_, y_}, {w_, h_}] :=
Module[{temptile, addrowsa, addrowsb},
temptile =
MapThread[
Join, {Table[0, {Dimensions[tile][[1]]}, {x - 1}], tile,
Table[0, {Dimensions[tile][[
1]]}, {w - (x - 1 + Dimensions[tile][[2]])}]
}
];
addrowsa = Table[0, {y - 1}, {w}];
addrowsb = Table[0, {h - (y - 1 + Dimensions[tile][[1]])}, {w}];
Join[addrowsa, temptile, addrowsb]
]
Returns a matrix with tile positioned at (x,y) in a h x w matrix and having 0s everywhere else.
usedSpace[universe_] := Module[{xRange, yRange, selectedRows},
xRange = MinMax[Last /@ Position[space, 1]];
yRange = MinMax[First /@ Position[space, 1]];
selectedRows = Take[universe, yRange];
Map[Take[#, xRange] &, selectedRows]
]
Returns the spanning rectangle of the tilled region in the universe.
usedRange[universe_] := {MinMax[Last /@ Position[universe, 1]],
MinMax[First /@ Position[universe, 1]]}
Returns the x and y ranges of the spanning rectangle of the tilled region in the universe.
findPerimeter[universe_] :=
Position[Erosion[universe, 1] - Erosion[universe, 2], 1]
Finds the points along the boundary of the tilled region in the universe.
scanRange[tile_, space_] := Module[{xRange, yRange, h, w, hMax, wMax,},
xRange = usedRange[space][[1]];
yRange = usedRange[space][[2]];
{h, w} = Dimensions[tile];
{hMax, wMax} = Dimensions[space];
{{Max[xRange[[1]] - w, 1],
Min[xRange[[2]] + 1, wMax - w + 1]}, {Max[yRange[[1]] - h, 1],
Min[yRange[[2]] + 1, hMax - h + 1]}}
]
Returns the x and y range of the region to be scanned for the tile in the space, where space is any (square) part of the universe.
addTile[tile_, region_, {x_, y_}] := Module[{},
If[overlapQ[tile, region, {x, y}] == True, 0,
space + positionTile[tile, {x, y}, Dimensions[region]]
]
]
Returns a matrix with the tile added to the region at (x,y) position. Returns 0 if the addition of tile fails. Region is any (square) part of the universe.
detectVoid[region_] := Module[{selectedRegion},
selectedRegion = usedSpace[region];
! (Values@ComponentMeasurements[selectedRegion, "Count"] ==
Values@ComponentMeasurements[selectedRegion, "FilledCount"])
]
Returns true if there is a void in the region, false otherwise.
score[region] := Module[{xRange, yRange},
If[region == 0, Return[Infinity];];
If[TrueQ[detectVoid[region]], Infinity,
{xRange, yRange} = usedRange[region];
First[(Differences[xRange] + 1)*(Differences[yRange] + 1)]
]
]
Gives the area of the spanning rectangle of the tilled space in the region.
scoreImg[region_] :=
Max[1 - ImageData[
Blur[Downsample[Rasterize[ArrayPlot[region]], 5, 5], 20]]]
Gives the score of the region calculated using image blur.
addNextTile[region_, tiles_] :=
Module[{minScores, regiontoscan, scores, scoresImg, newPos },
SetSharedVariable[minScores];
minScores = {};
ParallelMap[
tile = #;
regiontoscan = scanRange[tile, region];
scores =
Transpose[
Table[score[addTile[tile, region, {x, y}]], {x,
regiontoscan[[1, 1]], regiontoscan[[1, 2]]}, {y,
regiontoscan[[2, 1]], regiontoscan[[2, 2]]}]];
scoresImg =
Transpose[
Table[scoreImg[addTile[tile, region, {x, y}]], {x,
regiontoscan[[1, 1]], regiontoscan[[1, 2]]}, {y,
regiontoscan[[2, 1]], regiontoscan[[2, 2]]}]];
scores =
scores/Max[Cases[Join[scores, {1}], _Integer]]*(1 - scoresImg);
newPos =
Reverse[First[Take[Position[scores, Min[scores]], 1]]] +
First /@ regiontoscan - {1, 1};
AppendTo[minScores, {Min[scores], addTile[tile, region, newPos]}];
&, tiles];
First[SortBy[minScores, #[[1]] &]][[2]]
]
Adds a tile in optimum manner (using both the scores) to the region.
putUniverse[universe_, region_, {offsetx_, offsety_}] := Module[{},
For[j = offsety, j <= offsety + Dimensions[region][[1]] - 1, j++,
universe[[j]][[
offsetx ;; (offsetx + Dimensions[region][[2]] - 1)]] =
space[[j - offsety + 1]];
];
universe // ArrayPlot
]
Replaces the cells in universe with those in region starting at position (x,y).
takeUniverse[universe_, {offsetx_, offsety_}, {width_, height_}] :=
Module[{xRange, yRange, selectedRows},
xRange = {offsetx, offsetx + width - 1};
yRange = {offsety, offsety + height - 1};
selectedRows = Take[universe, yRange];
Map[Take[#, xRange] &, selectedRows]
]
Returns (as a matrix) a part of universe with dimensions height x width starting at position (offsetx,offsety).
increaseSpace[universe_, d_, l_] := Module[{newSpace, addrows},
Switch[d,
1,
addrows = Table[0, {l}, {Dimensions[universe][[2]]}];
newSpace = Join[addrows, universe];,
3,
addrows = Table[0, {l}, {Dimensions[universe][[2]]}];
newSpace = Join[universe, addrows];,
2,
newSpace =
MapThread[
Join, {universe, Table[0, {Dimensions[universe][[1]]}, {l}]}];,
4,
newSpace =
MapThread[Join, {Table[0, {Dimensions[universe][[1]]}, {l}], universe}];
];
newSpace
]
Expands the universe in d direction (1,2,3,4 clockwise starting from top) by adding l empty rows/columns.
trygrowUniverse[universe_, tiles_, {offsetx_, offsety_}] :=
Module[{dimension, usedrange, ibound, spaced},
dimension = Ceiling[1.5*(First /@ Dimensions /@ tiles // Max)];
usedrange = usedRange[universe];
ibound = innerBound[universe];
spaced =
takeUniverse[
universe, {offsetx, offsety}, {dimension, dimension}];
addNextTilewCost[spaced, tiles]
]
Gives the score of the arrangement after adding a tile in optimum position in a square of side dimension in the universe at position (offsetx, offsety)
growUniverse[universe_, tiles_, visualUniverse_] :=
Module[{minMinScores, offset},
universeBackup = universe;
SetSharedVariable[minMinScores];
minMinScores = {};
Map[
offset = #;
AppendTo[minMinScores, trygrowUniverse[universe, tiles, offset]];
&,
Position[Erosion[universe, 1] - Erosion[universe, 2], 1]
];
universe = First[SortBy[minMinScores, #[[1]] &]][[2]];
visualUniverse =
visualUniverse + RandomReal[]*(universe - universeBackup);
]
Adds a new tile along the boundary of the tilled region in universe, and updates visualUniverse.
The entire code can be found on GitHub