This is the best I could get using this model
deltaData = {{1.00, 0}, {0.96, 0.3416}, {0.92, 0.4749}, {0.88,
0.5715}, {0.84, 0.648}, {0.80, 0.711}, {0.76, 0.764}, {0.72,
0.8089}, {0.66, 0.864}, {0.62, 0.8939}, {0.58, 0.919}, {0.54,
0.9399}, {0.50, 0.9569}, {0.46, 0.9704}, {0.42, 0.9809}, {0.38,
0.9885}, {0.34, 0.9938}, {0.30, 0.9971}, {0.26, 0.9989}, {0.22,
0.9997}, {0.16, 1}, {0.14, 1}};
deltaFit =
NonlinearModelFit[
deltaData, (1 + a*T + c*T^2 + e*T^3 + g*T^4 + i*T^5 + k*T^6)/(1 +
b*T + d*T^2 + f*T^3 + h*T^4 + j*T^5 + l*T^6), {a, b, c, d, e, f,
g, h, i, j, k, l}, T];
Plot[deltaFit[T], {T, 0, 1}]
data = {{0.203, 0.031}, {0.203, 0.030}, {0.246, 0.055}, {0.267,
0.072}, {0.300, 0.105}, {0.300, 0.105}, {0.330, 0.147}, {0.373,
0.214}, {0.397, 0.255}, {0.415, 0.293}, {0.445, 0.351}, {0.477,
0.430}, {0.493, 0.463}, {0.520, 0.538}, {0.541, 0.590}, {0.582,
0.717}, {0.589, 0.733}, {0.625, 0.847}, {0.645, 0.911}, {0.685,
1.029}, {0.688, 1.043}, {0.730, 1.181}, {0.751, 1.247}, {0.782,
1.338}, {0.793, 1.375}, {0.830, 1.472}, {0.856, 1.531}, {0.878,
1.585}};
AlphaBCS = 1.746;
delta[T_, p_, alpha_] := p*deltaFit[T] + (1 - p)*deltaFit[T]/alpha;
fx[T_, x_, p_,
alpha_] := (Exp[AlphaBCS/T*(x^2 + delta[T, p, alpha]^2)^(1/2)] +
1)^(-1);
Ses[T_, p_, alpha_] := -6*AlphaBCS/Pi^2*
NIntegrate[
fx[T, x, p, alpha]*
Log[fx[T, x, p, alpha]] + (1 - fx[T, x, p, alpha])*
Log[1 - fx[T, x, p, alpha]], {x, 0, 10}, AccuracyGoal -> 5];
ces = D[fx[T, x, p, alpha]*
Log[fx[T, x, p, alpha]] + (1 - fx[T, x, p, alpha])*
Log[1 - fx[T, x, p, alpha]], T];
Ces[T0_, p0_, alpha0_] := -6*AlphaBCS/Pi^2*T0*
NIntegrate[ces /. {T -> T0, p -> p0, alpha -> alpha0}, {x, 0, 10},
AccuracyGoal -> 5]
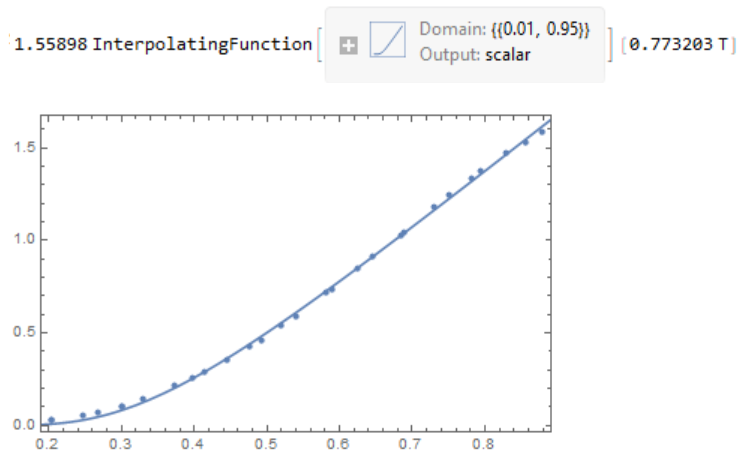
ff = Interpolation[Table[{t, Ces[t, .5, 1.764]}, {t, 0.01, .95, .01}]];nlm = NonlinearModelFit[data, a*ff[T*b], {{a, 1}, {b, 1}}, T];
Normal[nlm]
Show[ListPlot[data], Plot[nlm[T], {T, 0.015, .95}], Frame -> True]