Introduction
In Stephen Wolfram's book A New Kind of Science, he discovered a function that he conjectures to have some very special properties. He conjectures that for only positive inputs, all of the positive outputs produce Fibonacci Numbers, where each successive element greater than or equal to 3 is the sum of its previous elements. The function which he discovered follows as such: (2-(x^2-y^2-xy)^2)x 
This post will go through the proof that that specific Diophantine Equation produces Fibonacci Numbers for positive inputs and outputs. The goal of this post is to show a method that can be used to prove Dr Wolfram's Conjecture.
Proof
If we analyze the x^2-y^2-xy part, if this is an integer K such that K^2<2, then we will have discovered what x and y values satisfy the initial conditions stated above. The only integers squared that is less than 2 are 1, 0, and -1 (We can have a negative value because it will be squared).
So, using Mathematica, we can find the x and y values satisfying the conditions: First setting x^2-y^2-xy equal to 0 and solving: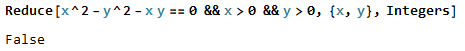 
Now setting x^2-y^2-xy equal to 1 and solving: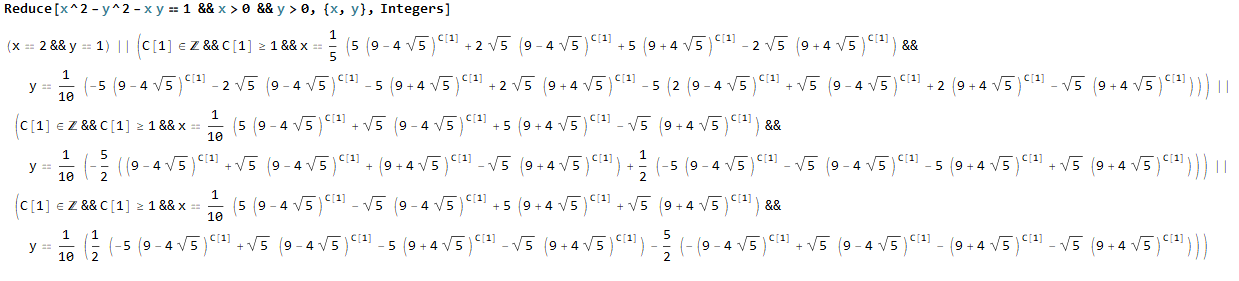 
Now setting x^2-y^2-xy equal to -1 and solving: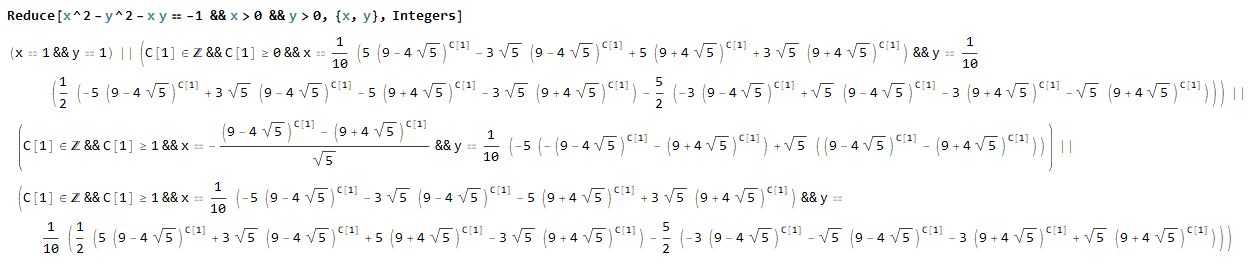 
We know that the first 100 Fibonacci Numbers are {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, 1346269, 2178309, 3524578, 5702887, 9227465, 14930352, 24157817, 39088169, 63245986, 102334155, 165580141, 267914296, 433494437, 701408733, 1134903170, 1836311903, 2971215073, 4807526976, 7778742049, 12586269025, 20365011074, 32951280099, 53316291173, 86267571272, 139583862445, 225851433717, 365435296162, 591286729879, 956722026041, 1548008755920, 2504730781961, 4052739537881, 6557470319842, 10610209857723, 17167680177565, 27777890035288, 44945570212853, 72723460248141, 117669030460994, 190392490709135, 308061521170129, 498454011879264, 806515533049393, 1304969544928657, 2111485077978050, 3416454622906707, 5527939700884757, 8944394323791464, 14472334024676221, 23416728348467685, 37889062373143906, 61305790721611591, 99194853094755497, 160500643816367088, 259695496911122585, 420196140727489673, 679891637638612258, 1100087778366101931, 1779979416004714189, 2880067194370816120, 4660046610375530309, 7540113804746346429, 12200160415121876738, 19740274219868223167, 31940434634990099905, 51680708854858323072, 83621143489848422977, 135301852344706746049, 218922995834555169026, 354224848179261915075}
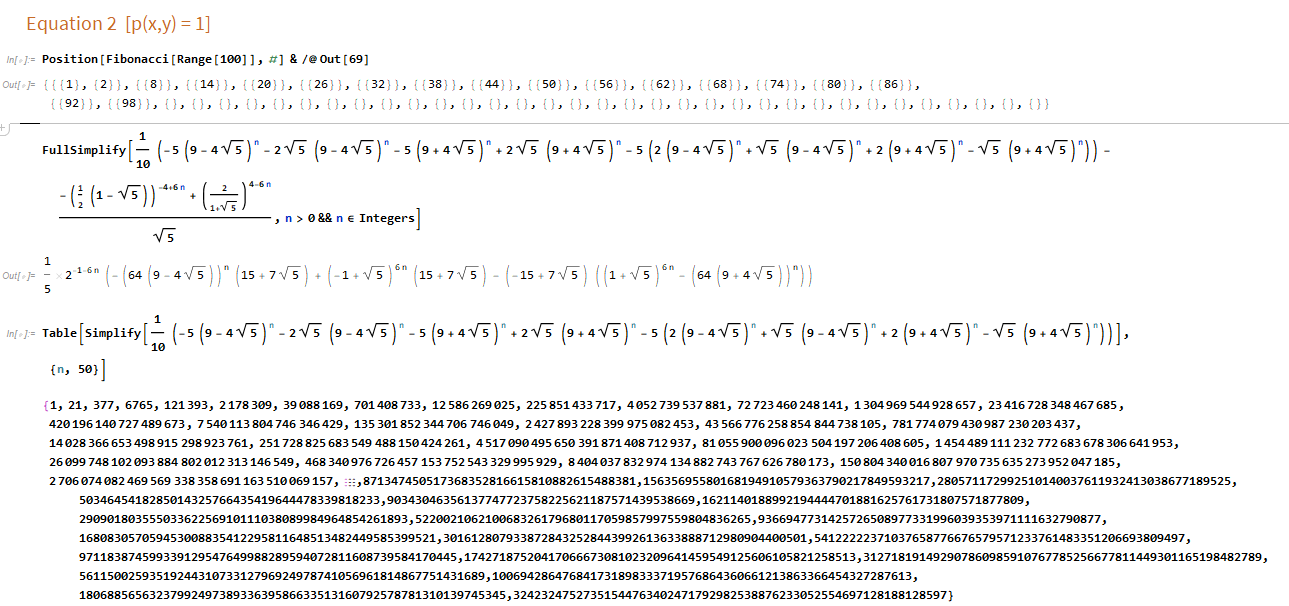
Now if we solve the first equation for the first 50 outputs we get: 
It can be seen that the equation produces every sixth Fibonacci number starting from the third element so using Binet's formula to produce every nth Fibonacci, by making these two equations equal each other, it can be proven that the equation (left) produces only Fibonacci numbers. 
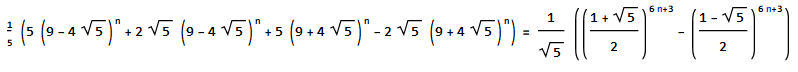We must show that the above equation is true, and takes on the form, 
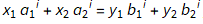, and that 
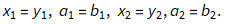Setting 
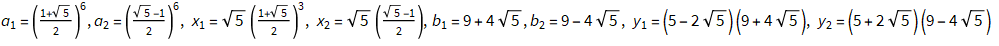, we can do the following:
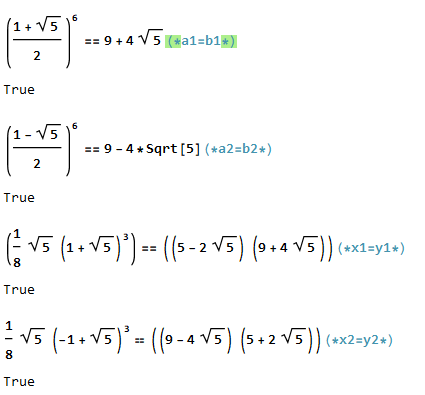
Following that logic, the proof can be extended to the other 11 equations as shown below:
The code for the remaining proofs has been attached to this post.
Attachments:
