Just need to make sure the B.C. and the I.C.'s are consistent. Here is an example with boundary condition at x=0 which is sin function.
eq = D[y[x, t], t, t] == D[y[x, t], x, x];
bc = {y[0, t] == t Sin[t], y[2 Pi, t] == 0};
ic = {y[x, 0] == Sin[x], (D[y[x, t], t] /. t -> 0) == 0};
sol = NDSolve[Flatten@{eq, ic, bc}, y, {x, 0, 2 Pi }, {t, 0, 10}]
which gives
{{y->InterpolatingFunction[{{0.,6.28318530717959},{0.,10.}},<>]}}
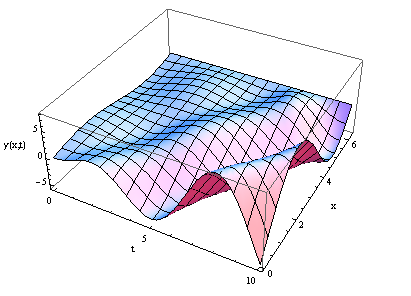
Now you can plot the solution
Plot3D[Evaluate[y[x, t] /. sol], {t, 0, 10}, {x, 0, 2 Pi },
PlotRange -> All, AxesLabel -> {"t", "x", "y(x,t)"}]
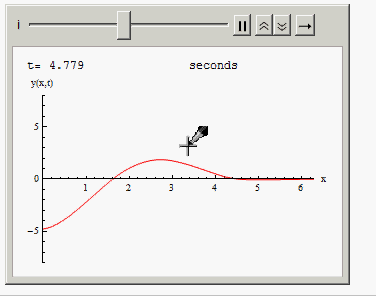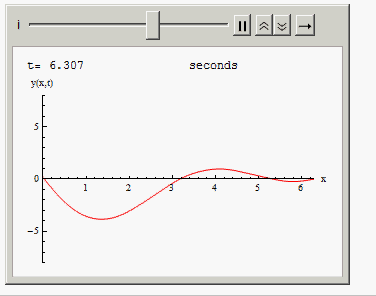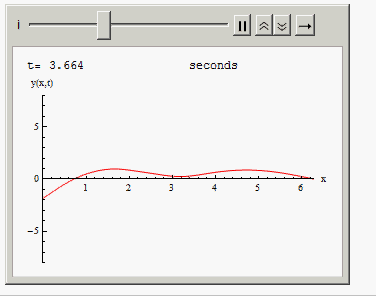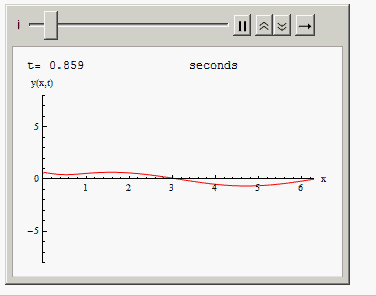
Or you can animate the solution in time:
Animate[Grid[{{"t=", i, " seconds"},
{Plot[Evaluate[y[x, t] /. sol /. t -> i], {x, 0, 2 Pi },
PlotRange -> {{0, 2 Pi}, {-8, 8}}, AxesLabel -> {"x", "y(x,t)"},
ImageSize -> 300, PlotStyle -> Red], SpanFromLeft}}], {i, 0,10, .001}]