Let's again consider the "Miss Brasilia", "Miss Australia" case:
Clear[l1, l2, x1, x2, r, pinkify]
l1 = "Miss Australia";
l2 = "Miss Brasilia";
x1 = ToCharacterCode[l1];
x2 = ToCharacterCode[l2];
pinkify[m_] := Block[{m1 = m, m2 = m, p = Position[m, 1], o, po},
For[o = 1, o <= Length[p], o++,
po = p[[o]];
If[Position[m1[[1 ;; po[[1]], po[[2]]]], 1, {1}, 1][[1, 1]] ==
po[[1]]
&& Position[m1[[po[[1]], 1 ;; po[[2]]]], 1, {1}, 1][[1, 1]] ==
po[[2]],
m2[[po[[1]], po[[2]]]] =
Item[m[[po[[1]], po[[2]]]], Background -> Green], (* else *)
m2[[po[[1]], po[[2]]]] =
Item[m[[po[[1]], po[[2]]]], Background -> Pink];
m1[[po[[1]], po[[2]]]] = 0
]
];
m2
] /; MatrixQ[m]
With[{r = Floor[Max[StringLength[l1], StringLength[l2]]/2] - 1},
Grid[pinkify[Normal[
SparseArray[
Join[
Table[Rule[{1, 1 + o}, Characters[l1][[o]]], {o,
StringLength[l1]}],
Table[
Rule[{1 + o, 1}, Characters[l2][[o]]], {o, StringLength[l2]}],
Flatten[
Table[Rule[{1 + o2, 1 + o1},
If[x1[[o1]] == x2[[o2]] && r >= Abs[o1 - o2], 1, 0]], {o2,
StringLength[l2]}, {o1, StringLength[l1]}], 1]
]
]
]
],
Frame -> All, ItemSize -> {3/2, 4/3}, Alignment -> Center
]
]
resulting in
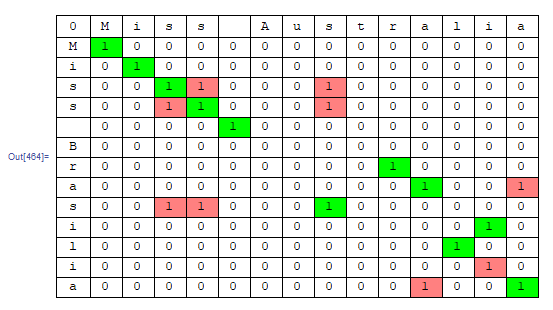
the pink 1do not go into the count, because they are not the rolling first ones in both directions seen from the beginning. One is left with m = 11, 6 perfect matches and 5 mismatches. This would count for a 2 t = 5 = 11 - 6, whereas the python implementation has 2 t = 4. This raises the idea, that not all mismatches must be count, but the existence of some permutation of more than 3 characters has to be realized, making the implemention more complex, as follows:
Clear[jaro]
jaro[s1_String, s2_String, prec_: $MachinePrecision] :=
Block[{r, l1 = StringLength[s1], l2 = StringLength[s2], l3, m, t},
r = Floor[Max[l1, l2]/2] - 1;
If[r >= 0,(* then *)
l3 = DeleteDuplicates[
Flatten[check[{Transpose[{ToCharacterCode[s1],
Range[l1]}][[#]]},
Transpose[{ToCharacterCode[s2], Range[l2]}][[
Min[l2, Max[1, # - r]] ;; Min[l2, # + r]]]] & /@ Range[l1],
1], ((First[#1] == First[#2]) || (Last[#1] == Last[#2])) &];
m = Length[l3];
If[m > 0,
t = share[
MapAt[First,
SortBy[#, Last] & /@ Transpose[l3], {{1, All}, {2, All}}]]/2;
N[(m/l1 + m/l2 + (m - t)/m)/3, prec], (* else *)
0
], (* else *)
0
]
] /; StringLength[s1] > 0 && StringLength[s2] > 0 && prec > 1
with the function share[], taking care for correspondances between the both strings of matching characters as well as for a rolling remapping for partnerless characters:
Clear[share]
share::insane = "x `1` as `2` is not bijective above 0";
share[l1_List, l2_List] :=
Block[{m = Length[l1], t = 0, x1, x2, o1, x3, o2, o3, z, seqL = 0, r,
r0, recycleQ, o4},
(* search for maximal connected sets of equal characters and denote \
them # - 1 as t *)
x1 = ConstantArray[0, m];
x2 = ConstantArray[0, m];
For[o1 = 1, o1 <= m, o1++,
x3 = Position[x2, 0, {1}, 1];
If[TensorRank[x3] == 2,
For[o2 = x3[[1, 1]], o2 <= m, o2++,
If[l2[[o2]] == l1[[o1]] && x2[[o2]] == 0,
If[o1 == o2,
x1[[o1]] = -1;
x2[[o2]] = -1, (* else *)
If[l1[[o2]] == l2[[o2]],
x1[[o2]] = -1;
x2[[o2]] = -1, (* else *)
If[l1[[o1]] == l2[[o1]],
x1[[o1]] = -1;
x2[[o1]] = -1, (* else *)
x2[[o2]] = o1;
x1[[o1]] = o2;
Break[]
]
]
]
]
]
]
];
For[o1 = 1, o1 <= m, o1++,
If[x1[[o1]] > 0,
If[x2[[o1]] > 0,
seqL += 1, (* else *)
z = l1[[o1]];
o2 = o1 + 1;
r = -1; recycleQ = True;
While[r != 0,
o4 = Position[x1[[o2 ;;]], -1, {1}, 1];
o4 = If[TensorRank[o4] == 2, o4[[1, 1]] - 1, m];
If[FreeQ[l1[[o2 ;; o4]], z],
If[x1[[o2 - 1]] > o2 - 1, x2[[x1[[o2 - 1]]]] = 0];
r = 0,(* else *)
o3 = o2 - 1 + First[First[Position[l1[[o2 ;; o4]], z, {1}, 1]]];
r = x1[[o3]];
If[recycleQ,
x1[[o3]] = x1[[o2 - 1]];
x2[[x1[[o2 - 1]]]] = o3;
x1[[o2 - 1]] = 0;
recycleQ = False, (* else *)
x1[[o3]] = r0;
x2[[r0]] = o3
];
r0 = r;
o2 = Min[o3 + 1, m]
]
];
If[insaneQ[x1], Message[share::insane, 1, x1]];
If[insaneQ[x2], Message[share::insane, 2, x2]];
t += (detect[x1[[o1 - seqL ;; o1 - 1]],
x2[[o1 - seqL ;; o1 - 1]], o1 - seqL, o1 - 1] +
If[seqL > 0, 1, 0]);
seqL = 0
], (* else *)
If[x2[[o1]] > 0,
z = l2[[o1]];
o2 = o1 + 1;
r = -1; recycleQ = True;
While[r != 0,
o4 = Position[x2[[o2 ;;]], -1, {1}, 1];
o4 = If[TensorRank[o4] == 2, m, o4[[1, 1]] - 1, m];
If[FreeQ[l2[[o2 ;; o4]], z],
If[x2[[o2 - 1]] > o2 - 1, x1[[x2[[o2 - 1]]]] = 0];
r = 0, (* else *)
o3 = o2 - 1 + First[First[Position[l2[[o2 ;; o4]], z, {1}, 1]]];
r = x2[[o3]];
If[recycleQ,
x2[[o3]] = x2[[o2 - 1]];
x1[[x2[[o2 - 1]]]] = o3;
x2[[o2 - 1]] = 0;
recycleQ = False, (* else *)
x2[[o3]] = r0;
x1[[r0]] = o3;
];
r0 = r;
o2 = Min[o3 + 1, m]
]
];
If[insaneQ[x1], Message[share::insane, 1, x1]];
If[insaneQ[x2], Message[share::insane, 2, x2]];
t += (detect[x1[[o1 - seqL ;; o1 - 1]],
x2[[o1 - seqL ;; o1 - 1]], o1 - seqL, o1 - 1] +
If[seqL > 0, 1, 0]);
seqL = 0, (* else:
x1\[LeftDoubleBracket]o1\[RightDoubleBracket] \[LessEqual] 0,
x2\[LeftDoubleBracket]o1\[RightDoubleBracket] \[LessEqual] 0 *)
t += (detect[x1[[o1 - seqL ;; o1 - 1]],
x2[[o1 - seqL ;; o1 - 1]], o1 - seqL, o1 - 1] +
If[seqL > 0, 1, 0]);
seqL = 0
]
]
];
t + If[seqL > 0,
detect[x1[[o1 - seqL ;; o1 - 1]], x2[[o1 - seqL ;; o1 - 1]],
o1 - seqL, o1 - 1],
0] - Count[x1, -1]
]
share[{l1_List, l2_List}] :=
share[l1, l2] /;
Length[l1] == Length[l2] && Length[l1] > 0 && VectorQ[l1, NumberQ] &&
VectorQ[l2, NumberQ]
share[{l1_List, l2_List}] := 0 /; Length[l1] == 0 && Length[l2] == 0
share[] itself depends on dectect[]:
Clear[insaneQ, check, detectI, detect]
insaneQ[l1_List?VectorQ] := Block[{l = Fold[DeleteCases, l1, {-1, 0}]},
Length[DeleteDuplicates[l]] != Length[l]
]
check[l1_List, l2_List] :=
Flatten[Outer[List, l1, Select[l2, #[[1]] == l1[[1, 1]] &], 1], 1]
detectI[l1_List, l2_List, o1_Integer, o2_Integer] :=
Block[{m = Length[l1], permQ = True, o3},
If[o1 < o2,
(* Is l2 a permutation of l1 in Interval[{o1,o2}]? *)
For[o3 = 1, o3 <= m, o3++,
If[permQ,
permQ = (o1 <= l1[[o3]] <= o2) && (o1 <= l2[[o3]] <= o2)
]
];
If[m > 2 && permQ,(* "jaro" permutation exists *)
o2 - o1,(* else *)
o2 - o1 + 1
], (* else *)
1
]
]
detect[l1_List, l2_List, o1_Integer, o2_Integer] :=
Block[{m = Length[l1], x = 0, o3},
If[o1 < o2,
(* Contain l1,l2 a permutation of more than 2 characters? *)
For[o3 = 1, o3 <= m, o3++,
x += If[(o1 <= l1[[o3]] <= o2) && (o1 <= l2[[o3]] <= o2), 1, 0]
];
If[x > 2,(* "jaro" permutation exists *)
o2 - o1,(* else *)
o2 - o1 + 1
], (* else *)
1
]
]
if one would use detectI[] one would check for a complete permutation between matches. detect[] looks only for some (> 2) characters in both strings.
With this in place look into test cases:
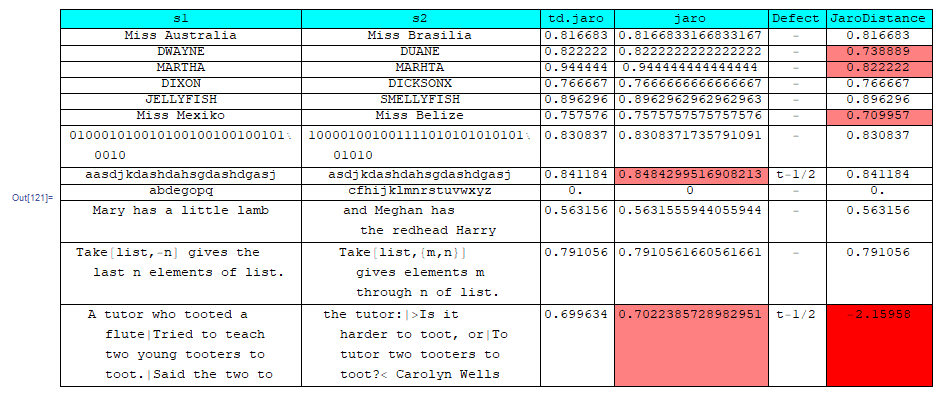
The first fail is bizarre, because it is a permutation, but other implementations have t bigger. The second fail could be fixed if one would use detectI[] instead of detect[], but then elsewhere fails show up.
For your convenience the notebook is in the appendix.
 Attachments:
Attachments: