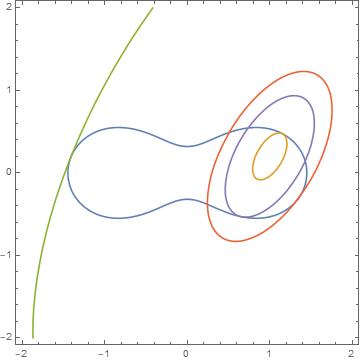
The goal is to find the largest ellipse (with given ratio of axes), centered at a given point and with a given orientatiion, that fits inside a specified non-convex oval.

 equation of oval

In[1]:= oval[{x_, y_}] = ((x - 1)^2 + y^2) ((x + 1)^2 + y^2) - (21/20)^4;

 derive equation of an ellipse with axes "a" and "b", centered at { xc, yc } 
with major axis making angle \[Theta] with x-axis.

In[2]:= Thread[{xel, yel} =  
   DiagonalMatrix[{a, b}^-1].RotationMatrix[-\[Theta]].{x - xc, y - yc}];

In[3]:= eleq[{{a_, b_}, xc_, yc_, \[Theta]_}, {x_, y_}] = xel^2 + yel^2 - 1;

 symbolically find largest ellipse with axes "a" and "a/2", 
centered at { 1, (1/5) } 
oriented at \[Pi]/3
RegionWithin takes about 1 minute.

In[4]:= AbsoluteTiming[
 RegionWithin[ImplicitRegion[oval[{x, y}] <= 0, {x, y}], 
   ImplicitRegion[eleq[{{a, a/2}, 1, 1/5, \[Pi]/3}, {x, y}] <= 0, {x, y}], 
   GenerateConditions -> True] // N]

Out[4]= {63.4787, 0. < a <= 0.315686 || -0.315686 <= a < 0.}

Calculating it numerically with a Lagrange multiplier 
and NSolve takes about 1 second.  
The desired answer is the one with the smallest value of a.

In[5]:= AbsoluteTiming[
 sln = NSolve[{a >= 0, oval[{x, y}] == 0, 
    eleq[{{a, a/2}, 1, 1/5, \[Pi]/3}, {x, y}] == 0, 
    Sequence @@ 
     D[oval[{x, 
         y}] == \[Lambda] eleq[{{a, a/2}, 1, 1/5, \[Pi]/3}, {x, y}], {{x, 
        y}}]}, {a, x, y, \[Lambda]}, Reals]]

Out[5]= {0.808361, {{a -> 0.315686, \[Lambda] -> 0.869176, x -> 1.15549, 
   y -> 0.474695}, {a -> 4.34436, \[Lambda] -> 7.03937, x -> -1.41308, 
   y -> 0.191823}, {a -> 0.817698, \[Lambda] -> 1.46331, x -> 0.654269, 
   y -> -0.531984}, {a -> 1.14366, \[Lambda] -> 1.77874, x -> 1.34316, 
   y -> -0.315728}}}

 eliminating the Lagrange multiplier before solving speeds up the calculation.

In[6]:= AbsoluteTiming[
 sln = NSolve[{a >= 0, oval[{x, y}] == 0, 
    eleq[{{a, a/2}, 1, 1/5, \[Pi]/3}, {x, y}] == 0, 
    Eliminate[ 
     D[oval[{x, 
         y}] == \[Lambda] eleq[{{a, a/2}, 1, 1/5, \[Pi]/3}, {x, y}], {{x, 
        y}}], \[Lambda]]}, {a, x, y}, Reals]]

Out[6]= {0.0641214, {{x -> 1.15549, y -> 0.474695, a -> 0.315686}, {x -> -1.41308, 
   y -> 0.191823, a -> 4.34436}, {x -> 1.34316, y -> -0.315728, 
   a -> 1.14366}, {x -> 0.654269, y -> -0.531984, a -> 0.817698}}}

 Plotting all the results show that the curves are tangent at the intersection point.