Introduction
Packing ellipses in a non-convex oval involves two problems: keeping the ellipses inside the oval and keep the ellipses disjoint. The basic approach for keeping the ellipses inside was discussed in a previous post
http://community.wolfram.com/groups/-/m/t/1453823
This function is applied to a group of discrete points, from which an interpolation function is created for use in the optimization.
Keeping the ellipses disjoint, a simpler problem, is done by using Lagrange multipliers to create constraints, see
http://www.optimization-online.org/DB_FILE/2016/03/5348.pdf
The optimization is done as as random searches using ParametricIPOPTMinimize.
ParametricIPOPT Code
In[1]:= Needs["IPOPTLink`"]
In[2]:= statusrl = {0 -> "Solve_Succeeded", 1 -> "Solved_To_Acceptable_Level",
2 -> "Infeasible_Problem_Detected",
3 -> "Search_Direction_Becomes_Too_Small", 4 -> "Diverging_Iterates",
5 -> "User_Requested_Stop",
6 -> "Feasible_Point_Found", -1 -> "Maximum_Iterations_Exceeded", -2 ->
"Restoration_Failed", -3 -> "Error_In_Step_Computation", -4 ->
"Maximum_CpuTime_Exceeded", -10 -> "Not_Enough_Degrees_Of_Freedom", -11 ->
"Invalid_Problem_Definition", -12 -> "Invalid_Option", -13 ->
"Invalid_Number_Detected", -100 -> "Unrecoverable_Exception", -101 ->
"NonIpopt_Exception_Thrown", -102 -> "Insufficient_Memory", -199 ->
"Internal_Error"};
In[3]:=
In[4]:= iMin[obj_, cons_List, vwb_List, nrands_Integer, seed_Integer, opts___] :=
Block[{lecons, vars, lbubs, cfuns, clbubs, v, lb, ub, params, param, pip,
starts, pres, listres, status, goodres, finalres},
lecons = cons /. {
( a_ == b_ ) -> LessEqual[0, a - b, 0],
( a_ <= b_ ) -> LessEqual[-\[Infinity], a - b, 0],
(a_ >= b_ ) -> LessEqual[0, a - b, \[Infinity]]
};
{vars, lbubs} = Transpose[vwb /.
{v_, lb_?NumericQ, ub_?NumericQ} :> {v, {lb, ub}}];
If[Length[cons] == 0, {cfuns, clbubs} = { {}, {} },
{cfuns, clbubs} =
Transpose[lecons /. LessEqual[lb_, v_, ub_] -> {v, {lb, ub}} ]
];
params = Table[param[i], {i, Length[vwb]}];
pip = ParametricIPOPTMinimize[obj, vars, params, lbubs, cfuns, clbubs,
params, "RuntimeOptions" -> {"WarningMessages" -> False}, opts];
SeedRandom[seed];
starts = Transpose[RandomReal[#, nrands] & /@ lbubs];
pres = pip @@@ starts;
listres = {IPOPTMinValue[#], IPOPTArgMin[#], IPOPTReturnCode[#]} & /@ pres;
IPOPTDataDelete /@ pres;
status = listres[[All, 3]];
Print[Tally[status] /. {s_, n_Integer} :> { s /. statusrl, n}];
goodres = Select[listres, Or[#[[3]] == 0, #[[3]] == 1] &];
finalres = If[Length[goodres] == 0,
listres[[Ordering[listres[[All, 1]]]]][[1]],
goodres[[ Ordering[goodres[[All, 1]]]]][[1]]
];
{finalres[[1]],
Thread[vars -> finalres[[2]]], finalres[[3]] /. statusrl}
]
Packing Code
equation of circumscribing oval is oval[{x,y}] == 0
In[5]:= oval[{x_, y_}] = ((x - 1)^2 + y^2) ((x + 1)^2 + y^2) - (21/20)^4;
code to generate equation of an ellipse with semi-major axes "a" and "b"
In[6]:= rottransrl[{xc_, yc_, \[Theta]_}, {x_, y_}] =
Thread[{x, y} -> RotationMatrix[-\[Theta]].{x - xc, y - yc}];
In[7]:= Thread[{xel, yel} =
DiagonalMatrix[{a, b}^-1].RotationMatrix[-\[Theta]].{x - xc, y - yc}];
In[8]:= ell[a_, b_][xc_, yc_, \[Theta]_][x_, y_] = xel^2 + yel^2 - 1;
eliminate \[Lambda] from Lagrange multiplier equation for minimizing size of ellipse with axes "a" and "a/2" that overlaps oval
In[9]:= eld = Eliminate[
D[oval[{x, y}] == \[Lambda] ell[a, a/2][xc, yc, \[Theta]][x, y], {{x,
y}}], \[Lambda]] // FullSimplify
Out[9]= 5 y (xc + x (-2 + x xc) + xc y^2) +
3 (-xc y + (2 x - xc) y (x^2 + y^2) - x (-1 + x^2 + y^2) yc) Cos[
2 \[Theta]] ==
5 x (-1 + x^2 + y^2) yc +
3 (x^4 - x^3 xc + x (xc - xc y^2) - y (1 + y^2) (y - yc) +
x^2 (-1 + y yc)) Sin[2 \[Theta]] && a != 0
define function using previous result without a!=0
In[10]:= el[xc_, yc_, \[Theta]_] = eld[[1]]
Out[10]= 5 y (xc + x (-2 + x xc) + xc y^2) +
3 (-xc y + (2 x - xc) y (x^2 + y^2) - x (-1 + x^2 + y^2) yc) Cos[
2 \[Theta]] ==
5 x (-1 + x^2 + y^2) yc +
3 (x^4 - x^3 xc + x (xc - xc y^2) - y (1 + y^2) (y - yc) +
x^2 (-1 + y yc)) Sin[2 \[Theta]]
define function to find larger axis of largest ellipse centered at {xc,yc} with orientation \[Theta] that finds inside oval.
Min is needed due to multiple solution of Lagrange multiplier equations.
In[11]:= dist[{xc_?NumericQ,
yc_?NumericQ, \[Theta]_?NumericQ}] := -N @ Sign[oval[{xc, yc}]]*
Min[a /. NSolve[{a >= 0,
oval[{x, y}] == 0,
ell[a, a/2][xc, yc, \[Theta]][x, y] == 0,
el[xc, yc, \[Theta]]},
{a, x, y}, Reals]]
evaluate the function at certain discrete values
In[12]:= AbsoluteTiming[
Quiet[disttblflat =
N @ Flatten[
Table[{xc, yc, \[Theta], dist[{xc, yc, \[Theta]}]}, {xc, -2, 2, 1/
10}, {yc, -1, 1, 1/10}, {\[Theta], 0, 2 \[Pi], \[Pi]/10}], 2]];]
Out[12]= {797.969, Null}
construct an interpolation function from the values at discrete points
In[13]:= Dimensions[
disttbl = disttblflat /. {a_?NumericQ, b_, c_, d_} :> {{a, b, c}, d}]
Out[13]= {18081, 2}
In[14]:= itbl = Interpolation[disttbl, InterpolationOrder -> 2];
area of the oval for calculating packing fraction
In[15]:= ovalarea = NIntegrate[Boole[oval[{x, y}] <= 0], {x, -2, 2}, {y, -2, 2}]
Out[15]= 2.56423
plot of the oval
In[16]:= ovalplot =
ContourPlot[Evaluate[oval[{x, y}] == 0], {x, -1.5, 1.5}, {y, -1.5, 1.5},
ImageSize -> Small, ContourStyle -> Red];
forall[vars, c == d, a <= b] using Lagrange multipliers
In[17]:= lagforall[LessEqual[a_, b_], Equal[c_, d_], vars_List] :=
{Flatten @ {LessEqual[a, b], Equal[c, d], \[Lambda] >= 0,
D[a - b == \[Lambda] (c - d), {vars}]} /. \[Lambda] -> \[Lambda][
Sequence @@ vars],
Join[vars, {\[Lambda][Sequence @@ vars]}]}
constraint for two curves to not overlap
In[18]:= curvesnooverlap[curve1_, {xc1_, yc1_, \[Theta]1_},
curve2_, {xc2_, yc2_, \[Theta]2_}, {x_, y_}] :=
lagforall[
0 <= curve1[xc1, yc1, \[Theta]1][x, y],
curve2[xc2, yc2, \[Theta]2][x, y] == 0,
{x, y}
]
no overlap constraint for two ellipses
In[19]:= noeqs[i_, j_] =
curvesnooverlap[ell[a, a/2], {xc[i], yc[i], \[Theta][i]},
ell[a, a/2], {xc[j], yc[j], \[Theta][j]}, {xno[i, j], yno[i, j]}];
all the constraints: all the ellipses fit into the oval and all are disjoint
In[20]:= cons[n_Integer] :=
Join[Table[a == itbl[xc[i], yc[i], \[Theta][i]], {i, n}],
Flatten[Table[Sequence @@ noeqs[i, j][[1]], {i, n - 1}, {j, i + 1, n}], 1]]
all the variables with bounds
In[21]:= vwb[n_Integer] :=
Join[{{a, 0, 1}}, Table[{xc[i], -1.5, 1.5}, {i, n}],
Table[{yc[i], -.5, .5}, {i, n}],
Table[{\[Theta][i], \[Pi]/2, 3 \[Pi]/2}, {i, n}],
Flatten[Table[{xno[i, j], -1.5, 1.5}, {i, n - 1}, {j, i + 1, n}], 1],
Flatten[Table[{yno[i, j], -.5, .5}, {i, n - 1}, {j, i + 1, n}], 1],
Flatten[Table[{\[Lambda][xno[i, j], yno[i, j]], 0, 5}, {i, n - 1}, {j,
i + 1, n}], 1]]
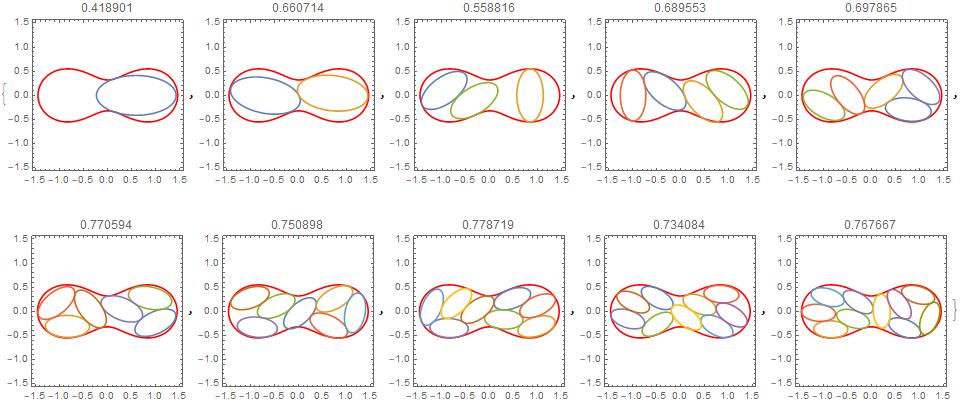
plotting function, putting packing fraction over plot
In[22]:= plt[n_Integer, sln_] :=
Show[ovalplot,
ContourPlot[
Evaluate[Table[ell[a, a/2][xc[i], yc[i], \[Theta][i]][x, y] == 0, {i, n}] /.
sln[[2]]], {x, -1.5, 1.5}, {y, -1.5, 1.5}],
PlotLabel -> ToString[ ((n*\[Pi] a a/2)/ovalarea /. sln[[2]])]
]
Packing Calculation
In[23]:= plts = Range[10];
In[24]:= AbsoluteTiming[plts[[1]] = plt[1, iMin[-a, cons[1], vwb[1], 100, 0]]];
During evaluation of In[24]:= {{Maximum_Iterations_Exceeded,3},{Solve_Succeeded,97}}
In[25]:= AbsoluteTiming[
Do[plts[[i]] = plt[i, iMin[-a, cons[i], vwb[i], 50, 0]], {i, 2, 10}]]
During evaluation of In[25]:= {{Solve_Succeeded,40},{Maximum_Iterations_Exceeded,5},{Infeasible_Problem_Detected,5}}
During evaluation of In[25]:= {{Maximum_Iterations_Exceeded,26},{Infeasible_Problem_Detected,13},{Restoration_Failed,1},{Solve_Succeeded,10}}
During evaluation of In[25]:= {{Maximum_Iterations_Exceeded,31},{Infeasible_Problem_Detected,12},{Solve_Succeeded,7}}
During evaluation of In[25]:= {{Maximum_Iterations_Exceeded,36},{Solve_Succeeded,9},{Infeasible_Problem_Detected,5}}
During evaluation of In[25]:= {{Solve_Succeeded,11},{Maximum_Iterations_Exceeded,34},{Infeasible_Problem_Detected,5}}
During evaluation of In[25]:= {{Maximum_Iterations_Exceeded,35},{Solve_Succeeded,9},{Infeasible_Problem_Detected,6}}
During evaluation of In[25]:= {{Maximum_Iterations_Exceeded,43},{Solve_Succeeded,6},{Infeasible_Problem_Detected,1}}
During evaluation of In[25]:= {{Maximum_Iterations_Exceeded,35},{Solve_Succeeded,8},{Infeasible_Problem_Detected,7}}
During evaluation of In[25]:= {{Maximum_Iterations_Exceeded,36},{Solve_Succeeded,7},{Infeasible_Problem_Detected,7}}
Out[25]= {3989.62, Null}
In[26]:= plts