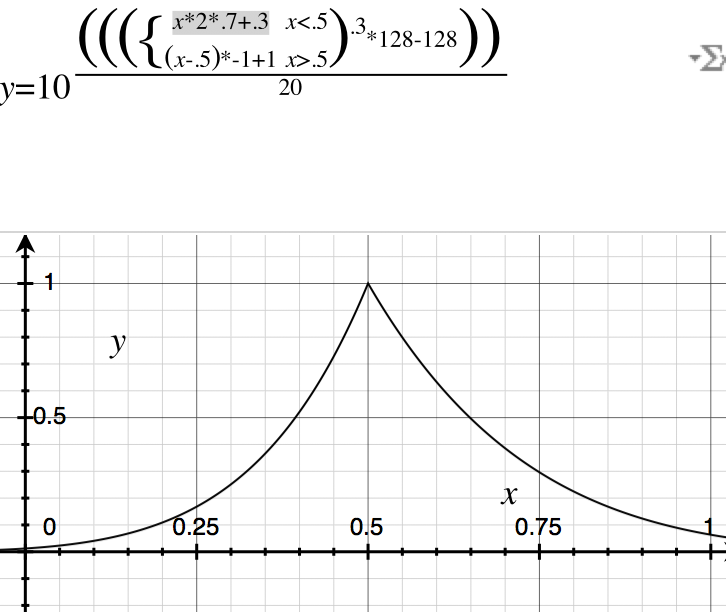
I'm trying to save some CPU cycles in an application by finding a curve formula that's "very similar but simpler" than the ones I have. I'm wondering what the best way to do this in Wolfram Alpha is. I tried to split it up into a table and then run cubic fit on it but Alpha wasn't really having that.
Any suggestions?
Here are the two formulas I'm attempting to approximate:
plot 10^((( (x*1.4+.3)^(.3) )*128-128)/20) from x=0 to 1
plot 10^((( (1-(x-.5))^.3 )*128-128)/20) from x=0 to 1
Here they are as tables:
Table[ 10^((( (x*1.4+.3)^(.3) )*128-128)/20) ,{x,0,1,.05}]
Table[ 10^((( (1-(x-.5))^.3 )*128-128)/20) ,{x,0,1,.05}]
And here's the syntax I tried.
quadratic fit[Table[ 10^((( (1-(x-.5))^.3 )*128-128)/20) ,{x,0,1,.05}]]
Here's what it looks like in Apple Grapher: