Hey Everyone! I'm currently working on a problem in a course on mathematical modeling concerning Outer Billiards. I'm supposed to write a program that does the following:
Start with a ball (a point particle) somewhere outside an equilateral triangle with side length equal to 1. You have two possibilities here and you select one of them. When it arrives at the corner it has traveled a distance d1. Then the particle continues in the same direction as before the same distance d1 There it changes direction momentarily and moves towards the other corner. Then the procedure is repeated, at the second corner it has traveled a distance d2 and it continues in the same direction the same distance d2, etc.
One problem that I've encountered is that for some points the trajectory of the point particle crosses the interior of the triangle, which is not allowed. Therefore I would like to create a test inside of my for loop which says that: "IF the trajectory towards a corner crosses the interior of the triangle, move instead to the next corner." Now, my lecturer gave me a hint that one can use determinants in order to make a pretty easy test, but I find it somewhat hard to understand intuitively. So I would like to make another test, but I don't know how exactly. Here is the program that I'm working on:
corner = {{1/2, Sqrt[3] /2}, {0, 0}, {1, 0}};
ourtriangle = Triangle[{corner[[1]], corner[[2]], corner[[3]]}];
p0 = {2, 2};
plotpoints = {p0};
cornerindex = 1;
n = 3;
For[i = 1, i < n, i++,
p1 = 2*corner[[cornerindex]] - p0;
p0 = p1;
AppendTo[plotpoints, p1];
cornerindex = Mod[i, 3] + 1;
]
traj = Table[plotpoints[[i]], {i, n}];
plot1 = Graphics[{Dashed, Line[traj]}];
Show[plot1, Graphics[ourtriangle], Axes -> False]
This yields the following graph: 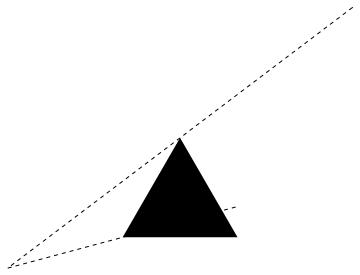
So, in this case I would like the trajectory to instead move towards the right-most corner but I really dont know how. Could someone please give me at least a hint?
Thank you all.