MIT's MPB and MEEP programs have a very interesting function called interpolate (and a variant kinterpolate-uniform), which basically creates points between a set of points, working like the Mathematica's Subdivide function.
Unfortunately Subdivide does not work with more than two vectors, subdividing only the endpoints. We can easily extend this behavior with the new functions:
SubdividePoints[pts_List?MatrixQ, n_Integer] := Block[{pt},
pt = Flatten[Table[
pts[[i]]*(1-t) + pts[[i+1]]*t
, {i, Length@pts-1}, {t, Subdivide[0,1,n+1]}]
, 1];
pt = Delete[pt, Position[Norm /@ Differences@pt, 0]]
]
And the another one for a uniform coverage.
SubdividePointsUniform[pts_List?MatrixQ, n_Integer] := Module[{L, m, pt},
L = (Norm /@ Differences@pts);
m = Round[L/Min[L/n]];
pt = Flatten[Table[
pts[[i]]*(1-t) + pts[[i+1]]*t
, {i, Length@pts-1}, {t, Subdivide[0,1,m[[i]]+1]}]
, 1];
pt = Delete[pt, Position[Norm /@ Differences@pt, 0]]
]
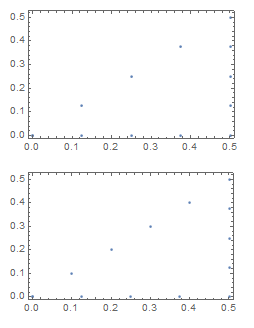
A simple example of usage would be creating points in the Brillouin zone of a square:
pts = {{0,0}, {1,0}, {1,1}, {0,0}}/2;
SubdividePoints[pts, 3] // ListPlot
SubdividePointsUniform[pts, 3] // ListPlot