I don't think this system has a solution (over the reals). If we define
f[?_, ?_] := 2 Cos[?] - 1.5 Sin[?] - 0.08 Cos[?]^2 + 0.08 Sin[?]^2 - 0.05 Cos[?/2]/?
g[?_, ?_] := 2 Sin[?] + 1.5 Cos[?] - 0.16 Cos[?] Sin[?] - Sin[?/2]
then we'd like to know where
f[?, ?] == g[?, ?] == 0
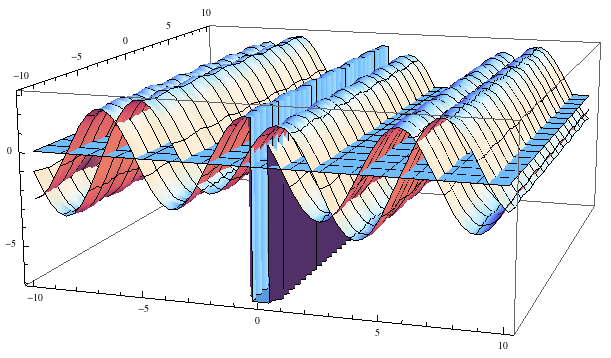
If we plot all three functions, it appears they don't simultaneously intersect.
Plot3D[{f[x, y], g[x, y], 0}, {x, -10, 10}, {y, -10, 10}]