Open in Cloud | Download to Desktop via Attachments Below

The following question appeared in Parade Magazine's Ask Marilyn column for Sunday, May 2, 2010:
A friend and I once went from his house to mine with one bicycle. I started walking and he rode the bike. When he got a couple of blocks ahead, he left the bike on the sidewalk and started walking. When I got to the bike, I started riding, passing him, and then left the bike a couple of blocks ahead. When he got to the bike, he started riding. We did this the whole way.
At least one of us was always walking. At times, one was riding; at other times, we were both walking. I'm sure this was faster than if we had no bike. But some people insist that it was no faster because somebody was always walking. Who's right?
Marilyn's answer was: "The reader is right. It's true that someone was always walking. But neither friend walked the whole distance. Both biked part of the way. This increased their average speed, so they saved time."
As with the Monty Hall problem, numerous readers wrote in to disagree with Marilyn, insisting that since someone was always walking, the journey could be no faster than if both had walked the entire distance. What do you think?
Designating the two friends as A and B, the situation is as follows (assuming A has the bike first):
A rides the bike and B walks, until A is a fixed distance h ahead of B, at which time A dismounts and leaves the bike on the sidewalk.
A and B walk until B comes to the bike, at which time B picks it up.
B rides the bike and A walks, until B is a distance h ahead of A, at which time B dismounts and leaves the bike on the sidewalk.
A and B walk until A gets to the bike, at which time A picks it up.
Step 1 follows Step 4, and the steps repeat sequentially until the last friend reaches the other house.
In his book Number-Crunching:Taming Unruly Computational Problems from Mathematical Physics to Science Fiction (which I highly recommend), Paul Nahin presents a Matlab program to simulate this problem. The program uses a discrete time step, and it occurred to me that with careful bookkeeping, the finish time (i.e., the time for the last friend to reach the house) could be calculated exactly. I decided to write my own simulation using Wolfram Mathematica. To begin, I define the following terms:
d: Distance between the two houses
h: Distance ahead, i.e., the rider leaves the bike this distance ahead of the walker
rA: Speed at which A rides the bike
wA: Speed at which A walks
rB: Speed at which B rides the bike
wB: Speed at which B walks
t : Time
$\Delta$t: Time increment
I also made the assumption that both friends are able to ride the bicycle faster than they walk, i.e., rA > wA and rB > wB.
In general, at the beginning of any step, A is at xA and B is at xB. At the end of the step, A is at xA + vA$\Delta$t and B is at xB + vB$\Delta$t, where A's velocity vA is either wA or rA depending on the particular step; B's velocity vB is either wB or rB; and $\Delta$t is calculated from the velocities and distances particular to that step. We must then check whether either of the two friends will reach the other house before $\Delta$t elapses.
The calculations for each step are as follows:
Step 1
When Step 1 is completed, A is h units ahead of B. Since A is riding the bike and B is walking, we have the equation xA + rA·$\Delta$t = xB + wB·$\Delta$t + h. Solving for $\Delta$t gives $\Delta$t = (xB - xA + h) / (rA - wB). Thus at the end of Step 1, A is at xA + rA·$\Delta$t, B is at xB + wB·$\Delta$t, and the time is incremented by $\Delta$t. A then puts down the bicycle.
Of course if rA $\leq$ wB then A will never catch up with B. The distance h essentially drops out of the problem, and the completion time is the time for A to ride the bike the entire distance d.
If xA + rA·$\Delta$t > d or xB + wB·$\Delta$t > d then one of the friends will reach the other house before the end of the time step. We must determine which friend arrives first; the total time for the journey is then the time at the beginning of Step 1 plus the time required for the other friend to reach the end of the journey.
Step 2
In Step 2, B walks the distance h and reaches the bike. This takes $\Delta$t = h/wB time units. At the end of Step 2, B is at xB + h, A is at xA + wA·$\Delta$t, and the time is incremented by $\Delta$t.
If xA + wA·$\Delta$t > d, then A reaches the other house on this step. The total time for the journey is then the current time plus the time required for B to get to the bike and ride it to the other house.
Step 3
Step 3 is identical to Step 1, except that B is riding the bike and A is walking. Reasoning as in Step 1, we find $\Delta$t = (xA - xB + h) / (rB - wA). So at the end of Step 3, A is at xA + wA·$\Delta$t, B is at xB + rB·$\Delta$t, and the time increments by $\Delta$t.
As in Step 1, if rB $\leq$ wA then B will never catch up to A, and the completion time is then the current time plus the time required for B to complete the journey on the bike.
If xA + wA·$\Delta$t > d or xB + rB·$\Delta$t > d, then one of the friends reaches the other house on this step. As in step 1, we determine which friend arrives first. The total time for the journey is then the time at the beginning of Step 3 plus the time required for the other friend to reach the other house. The time increments by $\Delta$t.
Step 4
Step 4 is identical to Step 2, except that A walks the distance h and reaches the bike. This takes $\Delta$t = h/wA time units. At the end of step 2, A is at xA + h, B is at xB + wB·$\Delta$t, and the time is incremented by $\Delta$t.
However, if xB + wB·$\Delta$t > d then B reaches the other house before A reaches the bike. So the total time to complete the journey is the time at the beginning of Step 4 plus the time required for A to get to the bike and ride it to the second house.
Finally we can translate these equations and conditions into the Wolfram language and write a function to determine the total time of the journey given wA, wB, rA, rB, d, and h:
tFinal[wA_, rA_, wB_, rB_, d_, h_] :=
Block[{t = 0, xA = 0, xB = 0, xC = 0, dt, dt2, dt4},
dt2 = h/wB; dt4 = h/wA;
While[True,
(* Step 1 *)
If[rA <= wB, Return[d/rA]];
dt = (h + xB - xA)/(rA - wB);
If[(xA + rA dt >= d ) || (xB + wB dt >= d),
If[(d - xA)/rA < (d - xB)/wB, Return[t + (d - xB)/wB],
Return[t + (d - xA)/rA]]];
xA += rA dt; xB += wB dt; xC = xA; t += dt;
(* Step 2 *)
dt = dt2;
If[xA + wA dt > d, Return[t + dt + (d - xC)/rB]];
xA += wA dt; xB += h; t += dt;
(* Step 3 *)
If[rB <= wA, Return[t + (d - xB)/rB]];
dt = (h + xA - xB)/(rB - wA);
If[(xB + rB dt >= d ) || (xA + wA dt >= d),
If[(d - xB)/rB < (d - xA)/wA, Return[t + (d - xA)/wA],
Return[t + (d - xB)/rB]]];
xB += rB dt; xA += wA dt; xC = xB; t += dt;
(* Step 4 *)
dt = dt4;
If[xB + wB dt >= d, Return[t + dt + (d - xC)/rA]];
xA += h; xB += wB dt; t += dt;]]
With this function we can reproduce Nahin's figure 7.2.2, with d = 1 mile, wA = wB = 2 miles per hour, and rA = rB = 6 miles per hour:
d = 5280.; wA = wB = 2*5280/3600; rA = rB = 6*5280/3600;
Plot[tFinal[wA, rA, wB, rB, d, h], {h, 10, 1500}, Frame -> True,
FrameLabel -> {"Separation (feet)",
"Time for second friend to finish (seconds)"},
LabelStyle -> Directive[Larger], GridLines -> None,
ImageSize -> Large, PlotLabel -> "Figure 1"]
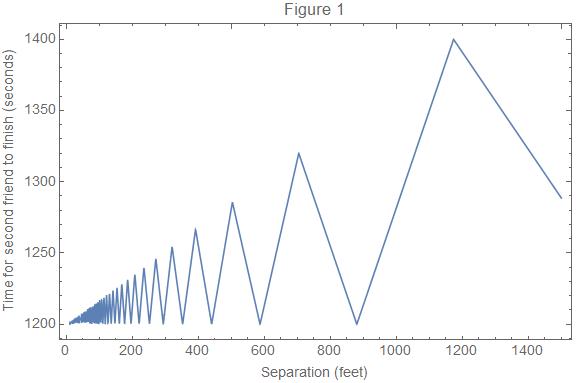
Given their walking speed of 2 miles per hour, it would take the friends 30 minutes = 1800 seconds to cover a distance of one mile without the bicycle. Figure 1 shows that there are values of h that result in times as low as 1200 seconds. Clearly, sharing the bicycle makes the journey faster. Marilyn Vos Savant was correct!
 Attachments:
Attachments: