For what purpose do you want a solution to this problem? Even in the simplest case, the solutions are very cumbersome. In my opinion, a numerical solution is preferable. I will give a working code that performs symbolic calculations for the numerical values of parameters
Subscript[U,
p] = (Sqrt[Da]
E^(-((Y Sqrt[\[Epsilon]])/Sqrt[
Da])) (-1 + E^((Y Sqrt[\[Epsilon]])/Sqrt[
Da])) (E^((Sqrt[\[Epsilon]] Subscript[y, p])/Sqrt[
Da]) (1 + E^((Y Sqrt[\[Epsilon]])/Sqrt[Da])) -
2 Da (E^((Y Sqrt[\[Epsilon]])/Sqrt[Da]) - E^((
Sqrt[\[Epsilon]] Subscript[y, p])/
Sqrt[Da])) (-1 + E^((
Sqrt[\[Epsilon]] Subscript[y, p])/Sqrt[Da])) -
2 Sqrt[Da] (E^((Y Sqrt[\[Epsilon]])/Sqrt[Da]) - E^((
2 Sqrt[\[Epsilon]] Subscript[y, p])/
Sqrt[Da])) \[Epsilon]^(
3/2) + Subscript[y,
p] (-2 E^((Sqrt[\[Epsilon]] Subscript[y, p])/Sqrt[Da]) +
2 Sqrt[Da] E^((Y Sqrt[\[Epsilon]])/Sqrt[Da]) \[Epsilon]^(
3/2) -
2 Sqrt[Da] E^((2 Sqrt[\[Epsilon]] Subscript[y, p])/
Sqrt[Da]) \[Epsilon]^(3/2) +
E^((Sqrt[\[Epsilon]] (Y + Subscript[y, p]))/Sqrt[
Da]) (-2 + Subscript[y, p]) +
E^((Sqrt[\[Epsilon]] Subscript[y, p])/Sqrt[Da]) Subscript[y,
p])))/(2 (-Sqrt[Da] + \[Epsilon]^(
3/2) - \[Epsilon]^(3/2) Subscript[y, p] +
E^((2 Sqrt[\[Epsilon]] Subscript[y, p])/Sqrt[
Da]) (Sqrt[Da] + \[Epsilon]^(
3/2) - \[Epsilon]^(3/2) Subscript[y, p])));
Subscript[U,
c] = ((-1 + Y) (Sqrt[Da] + Sqrt[Da] Y - 2 Da \[Epsilon]^(3/2) +
4 Da E^((Sqrt[\[Epsilon]] Subscript[y, p])/
Sqrt[Da]) \[Epsilon]^(
3/2) - Y \[Epsilon]^(3/2) -
2 Sqrt[Da] Subscript[y, p] + \[Epsilon]^(3/2) Subscript[y, p] +
Y \[Epsilon]^(3/2) Subscript[y, p] - \[Epsilon]^(3/2)
\!\(\*SubsuperscriptBox[\(y\), \(p\), \(2\)]\) -
E^((2 Sqrt[\[Epsilon]] Subscript[y, p])/Sqrt[
Da]) (Sqrt[Da] (1 + Y) + (2 Da + Y) \[Epsilon]^(
3/2) - (2 Sqrt[Da] + (1 + Y) \[Epsilon]^(3/2)) Subscript[
y,
p] + \[Epsilon]^(3/2)
\!\(\*SubsuperscriptBox[\(y\), \(p\), \(2\)]\))))/(
2 (-Sqrt[Da] + \[Epsilon]^(3/2) - \[Epsilon]^(3/2) Subscript[y,
p] +
E^((2 Sqrt[\[Epsilon]] Subscript[y, p])/Sqrt[
Da]) (Sqrt[Da] + \[Epsilon]^(
3/2) - \[Epsilon]^(3/2) Subscript[y, p])));
A = FullSimplify[D[Subscript[U, p], {Y, 2}]];
B = FullSimplify[D[Subscript[U, p], {Y, 1}] /. {Y -> 0}];
F = FullSimplify[
Integrate[Subscript[U, c]/Um, {Y, Subscript[y, p], 1}]];
G = FullSimplify[Subscript[U, p] /. {Y -> Subscript[y, p]}];
Subscript[y,
p] = .001; \[Epsilon] = .001; Da = 1; Bi = 1; k = 1; Um = 1;
s = DSolve[{D[X[Y], {Y, 4}] - (Bi*(1 + k))/k X''[Y] -
1/(k*Um) (A - Bi*Subscript[U, p]) == 0,
D[Z[Y], {Y, 4}] - (Bi*(1 + k))/k*Z''[Y] +
Bi/k*Subscript[U, p]/Um == 0,
Z''[Subscript[y, p]] == 0,
X[Subscript[y, p]] == XP, Z[Subscript[y, p]] == XP,
F == -k*X'[Subscript[y, p]] - Z'[Subscript[y, p]], X[0] == X0,
Z[0] == X0,
-k*X'[0] - Z'[0] == 1,
Bi*(Z'[0] + X'[0]) == D[Z[Y], {Y, 3}] /. Y -> 0}, {X[Y], Z[Y]}, Y];
x = X[Y] /. s; z = Z[Y] /. s;
x2p = D[x, Y, Y] /. Y -> Subscript[y, p];
x20 = D[x, Y, Y] /. Y -> 0;
x30 = D[x, {Y, 3}] /. Y -> 0;
x10 = D[x, Y] /. Y -> 0;
z10 = D[z, Y] /. Y -> 0;
x0 = First[X0 /. Solve[k*x2p == G/Um, X0]];
xp = First[XP /. Solve[k*x30 + Bi*(z10 - x10) == B/Um, XP]];
xpf = xp /. X0 -> x0;
xp0 = First[XP /. NSolve[XP == xpf, XP]];
x00 = x0 /. XP -> xp0;
This is the result of calculating dependencies XN=X[Y], ZN=Z[Y] with numerical coefficients.
XN = First[x /. {X0 -> x00, XP -> xp0} // FullSimplify]
Out[]= 2.11134*10^8 + (-124770. + 0.25 Y) Y -
499.75 Cosh[0.0316228 Y] + 361.302 Cosh[1.41421 Y] +
3.94494*10^6 Sinh[0.0316228 Y] + 120.434 Sinh[1.41421 Y]
ZN = First[z /. {X0 -> x00, XP -> xp0} // FullSimplify]
Out[]= 2.11134*10^8 + (-124812. + 0.25 Y) Y -
500.25 Cosh[0.0316228 Y] + 0.000625083 Cosh[1.41421 Y] +
3.94889*10^6 Sinh[0.0316228 Y] - 44.5035 Sinh[1.41421 Y]
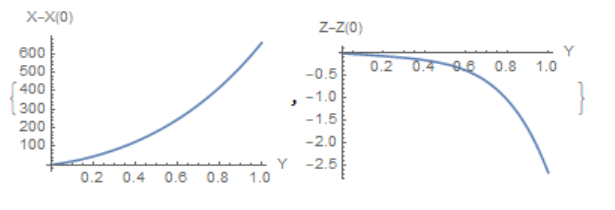
XN0 = XN /. Y -> 0; ZN0 = ZN /. Y -> 0;
{Plot[XN - XN0, {Y, 0, 1}, AxesLabel -> {"Y", "X-X(0)"}],
Plot[ZN - ZN0, {Y, 0, 1}, AxesLabel -> {"Y", "Z-Z(0)"}]}