For the following norm-preserving evolution of the quantum state in 2D Hilbert space: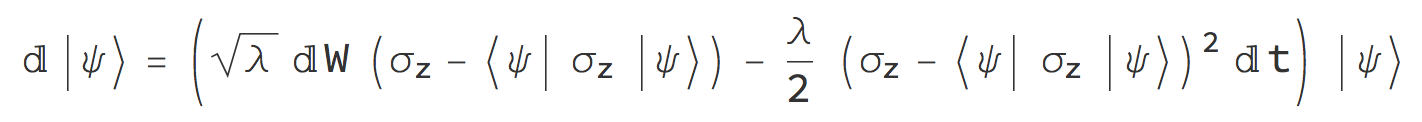 
with dW the usual Wiener increment, and |psi>={c1,c2}, I wrote this code:
collapseDynamics[\[Lambda]_, c10_, c20_] :=
ItoProcess[{\[DifferentialD]c1[
t] == -(\[Lambda]/
2) \[DifferentialD]t (c1[t] - 2 c1[t] (c1[t]^2 - c2[t]^2) +
c1[t] (c1[t]^2 - c2[t]^2)^2) + \[DifferentialD]W[
t] Sqrt[\[Lambda]] (c1[t] -
c1[t] (c1[t]^2 - c2[t]^2)), \[DifferentialD]c2[
t] == -(\[Lambda]/
2) \[DifferentialD]t (c2[t] + 2 c2[t] (c1[t]^2 - c2[t]^2) +
c2[t] (c1[t]^2 - c2[t]^2)^2) + \[DifferentialD]W[
t] Sqrt[\[Lambda]] (-c2[t] -
c2[t] (c1[t]^2 - c2[t]^2))}, {c1[t],
c2[t]}, {{c1, c2}, {c10, c20}}, {t, 0},
W \[Distributed] WienerProcess[]];
When I generate an evolution I noticed that the norm is not preserved:
data = RandomFunction[
collapseDynamics[1, 1/Sqrt[2], -1/Sqrt[2]], {0., 1, 0.01}];
ListLinePlot[Total /@ ((data["States"][[1]])^2), PlotRange -> All]
Can anyone explain why the norm is not preserved? (attached you can find nb file)
Attachments:
