To use Manipulate, need to decide which are the "control" variables. These are the variables you'd like to change during the simulation. i.e. the ones that have a slider or check box, etc... associated with them. In your case, you just then need one control variable, which is time range. In this case you can write
Manipulate[
Plot[Sin[60*Pi*t]+Sin[64*Pi*t],{t,0,tMax},
Frame->True,
FrameLabel->{{"f(t)",None},{"time (sec)",None}},
BaseStyle->14,
PlotStyle->Red,
GridLines->Automatic,GridLinesStyle->LightGray,
PlotRange->{Automatic,{-2.1,2.1}},
ImageSize->400]
,
{{tMax,1,"time"},0,1.5},
Alignment->Center,
ImageMargins->0,
FrameMargins->0,
Paneled->True,
Frame->False,
SynchronousUpdating->False,SynchronousInitialization->False
]
which gives
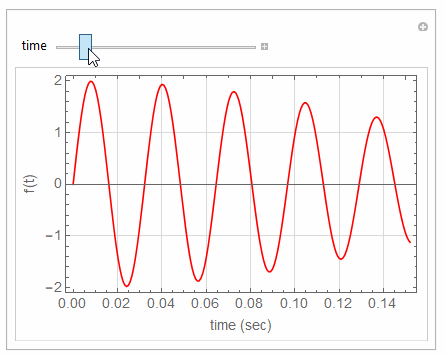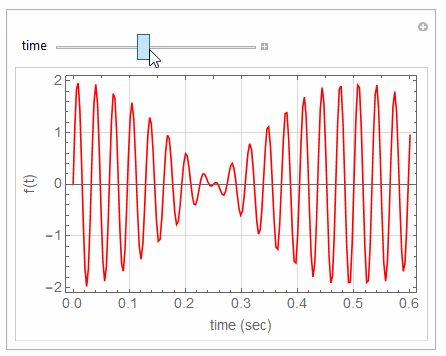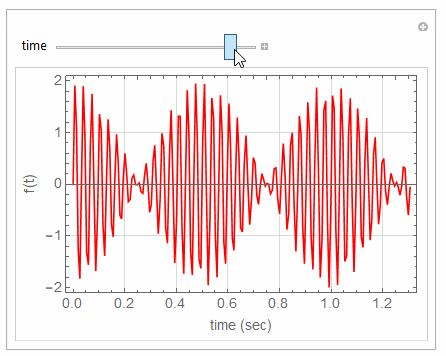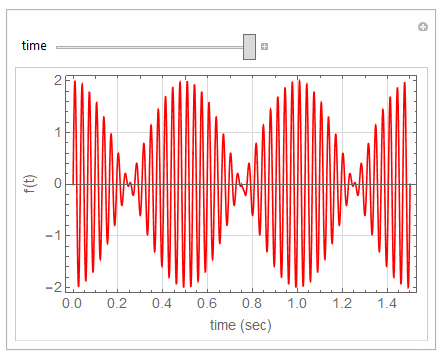
If you want also to change say the frequency and see what happens, then add another control variable and make new slider, and so on.