Hi all, I was trying to use Mathematica for preprocessing to generate a Voronoi mesh with assigned values. Here is my code to generate the mesh:
noPoly = 20; boxSize = 400; pts =
RandomReal[{-boxSize, boxSize}, {noPoly, 2}]; mesh =
VoronoiMesh[pts, {{-boxSize, boxSize}, {-boxSize, boxSize}}]
You will get something like:
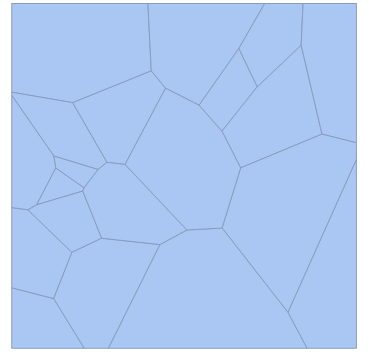
Now this is what I want to do:
1) For each "grain" in the diagram, I want to assign a constant value for the whole grain. i.e., define a function f(x,y) on the mesh such that it is constant in the same grain but maybe different for different grains.
2) Then I want to generate a list of x,y,f(x,y) for x,y are uniform grid points, like (1,0), (2,0), (1,1), (1,2).... If I can do this, I know how to generate text file for another software to read and generate this function.
2) is easy if I could do 1), i.e. get the function f(x,y). I have check the Mathematica documentation but have no idea how to do this. It seems PropertyValue might help but how? How do I even get those value defined on a mesh?
Thanks in advance!