The constants are a result of the physical problem that I'm trying to solve. I'm investigating temporal solitons in optical fibers (i.e., non-dispersive solitons in the time domain), and the dispersion of the mode of interest imposes the higher-order terms in the Nonlinear Schrödinger Equation. The actual values are associated with the fiber used and can changed if another configuration of fiber and pulse are used. Typically, these values are varied to find interesting fiber structures.

Hi Markus,

Could you provide an inefficient, but accurate, solution pointing out the key required features to capture? When I look at your solutions, it is clear that the low resolution case missed many spikey features. Do you care about those features? Does that imply that the high resolution solution is accurate? There is no point trying to speed up an inaccurate solution. Is there an area that you would like to resolve? Most of the action appears to be centered around low absolute $\tau$. What are you trying to resolve and has your approach resolved it or do we need to refine further?

I used the following plot functions to view your cases of MinPoints->600 and 2000, respectively.

plt = Plot3D[
  Evaluate[Abs[Us[\[Tau], \[Xi]]] /. 
    Last[sol]], {\[Tau], -\[Tau]max, \[Tau]max}, {\[Xi], 0, \[Xi]max},
   PlotPoints -> {100, 100}, MaxRecursion -> 4, 
  ColorFunction -> 
   Function[{x, y, z}, Directive[ColorData["DarkBands"][z]]], 
  ColorFunctionScaling -> False, MeshFunctions -> {#3 &}, Mesh -> 50, 
  PlotRange -> All, Boxed -> False, Axes -> False, ImageSize -> Large]

sz = 300;
Grid[{{Show[{plt}, ViewProjection -> "Orthographic", 
    ViewPoint -> Front, ImageSize -> sz, 
    Background -> RGBColor[0.84`, 0.92`, 1.`], Boxed -> False], 
   Show[{plt}, ViewProjection -> "Orthographic", ViewPoint -> Right, 
    ImageSize -> sz, Background -> RGBColor[0.84`, 0.92`, 1.`], 
    Boxed -> False]}, {Show[{plt}, ViewProjection -> "Orthographic", 
    ViewPoint -> Top, ImageSize -> sz, 
    Background -> RGBColor[0.84`, 0.92`, 1.`], Boxed -> False], 
   Show[{plt}, ViewProjection -> "Perspective", 
    ViewPoint -> {Above, Right, Front}, ImageSize -> sz, 
    Background -> RGBColor[0.84`, 0.92`, 1.`], Boxed -> False]}}, 
 Dividers -> Center]

Hi Res Grid

I indicated a "Hair Line" on the figure. I would have assumed it was a simulation artifact, but you might be trying to resolve it given your statement about "fission", but how would one know? I zoomed in on the right and left side.

Hi Res Right Zoom

Hi Res Left Zoom

Low Res Grid

If we zoom in on the $\tau$ scale, the instability for the low resolution is clearer.

Hi Res Zoom

Low Res Zoom

This may look like fission, but it is probably numerical. If we look at the underside of the Hi Res Zoom, we see some very sharp spikes that the solver needs to detect while solving before it can resolve.

You can view the adaptive mesh actions the solver took to resolve the spikes by selecting the Mesh->All option in Plot3D. If we zoom in on a spike, we can see the refinements.

In the low res case, the spike probably existed within a mesh element.

Applying a Window Function

For $\tau>5$, the Gaussian function is numerical insignificant relative to your range as alluded to by Alexander. Could we apply a window function using (UnitStep[4-$\tau>5$]-UnitStep[4+$\tau>5$])? When I do that with DifferenceOrder->4, all sorts of splitting happens (4 distinct peaks). Is that real? Also, the solution on my machine is about 3.5 x faster (20 seconds) than without the window function.

Clear["`*"]; ClearAll; ClearAll["Global\[OpenCurlyQuote]*"]; \
Remove["Global`*"];
SetDirectory[NotebookDirectory[]];

\[Delta]3 = 0.00404040404040404;
\[Delta]4 = -4.2087542087542085*^-6;
NS = 4.483404754211932;

\[Xi]max = 1;
\[Tau]max = 30;

Us1[\[Tau]_] = 
  Exp[-1.3862943611198906*\[Tau]^2] (UnitStep[5 - \[Tau]] + 
     UnitStep[5 + \[Tau]]);
Plot[Us1[\[Tau]], {\[Tau], -\[Tau]max, \[Tau]max}, Frame -> True, 
  PlotStyle -> Darker[Blue], PlotRange -> All, Filling -> Bottom];
eqs = {D[Us[\[Tau], \[Xi]] , \[Xi]] - 
     I/2*D[Us[\[Tau], \[Xi]], {\[Tau], 2}] - \[Delta]3*
      D[Us[\[Tau], \[Xi]], {\[Tau], 3}] - 
     I*\[Delta]4*D[Us[\[Tau], \[Xi]], {\[Tau], 4}] - 
     I*NS^2*Abs[Us[\[Tau], \[Xi]]]^2*Us[\[Tau], \[Xi]] == 0}; 
bc = {Us[\[Tau]max, \[Xi]] == 0, 
   Us[-\[Tau]max, \[Xi]] == 
    0, (D[Us[\[Tau], \[Xi]], {\[Tau], 1}] /. \[Tau] -> \[Tau]max) == 
    0, (D[Us[\[Tau], \[Xi]], {\[Tau], 1}] /. \[Tau] -> -\[Tau]max) == 
    0};
ic = {Us[\[Tau], 0] == Us1[\[Tau]]};
Print["seconds to obtain solution: ",
  time = AbsoluteTiming[
     Monitor[
       sol = 
        NDSolve[Join[eqs, ic, bc], 
         Us, {\[Tau], -\[Tau]max, \[Tau]max}, {\[Xi], 0, \[Xi]max}, 
         EvaluationMonitor :> (\[Xi]current = \[Xi]), 
         Method -> {"MethodOfLines", 
           "SpatialDiscretization" -> {"TensorProductGrid", 
             "MinPoints" -> 2000, "DifferenceOrder" -> 4}}, 
         PrecisionGoal -> 5, AccuracyGoal -> 5, 
         MaxSteps -> \[Infinity]], 
       "current \[Xi] (\!\(\*SubscriptBox[\(\[Xi]\), \(max\)]\)=" <> 
        ToString[\[Xi]max] <> "): " <> ToString[ \[Xi]current]];][[
    1]]] ;
Print["grid points along {\[Tau],\[Xi]}-directions: ", 
  Length /@ InterpolatingFunctionCoordinates[Us /. sol[[1]]]];

(UnitStep[4-$\tau$]-UnitStep[4+$\tau$])

(UnitStep[5-$\tau$]-UnitStep[5+$\tau$])

There seems to be minor change going from 4 to 5 on the window function, indicating little sensitivity in that range.

Zoomed

(UnitStep[6-$\tau$]-UnitStep[6+$\tau$])

Here is an animation along the $\xi$ coordinate for an alternative visualization.

Summary

We may or may not be making progress. Adding a window function when the Gaussian becomes insignificant, seems to induce splitting. We will need some more definition from you about your requirements and what the expected results are to make any additional progress. If we are on the right path, then a 20 seconds solve time should enable 4000 simulations per day.

Hi Markus,

I am about to head out for the evening, but here is an odd difference order attempt, which the documentation advise against, but it is fast (<6 seconds on my machine).

\[Delta]3 = 0;
\[Delta]4 = 0;
NS = 4;

\[Xi]max = 0.6;
\[Tau]max = 10;

Us1[\[Tau]_] = Exp[-1.3862943611198906*\[Tau]^2];
Plot[Us1[\[Tau]], {\[Tau], -\[Tau]max, \[Tau]max}, Frame -> True, 
  PlotStyle -> Darker[Blue], PlotRange -> All, Filling -> Bottom];
eqs = {D[Us[\[Tau], \[Xi]] , \[Xi]] - 
     I/2*D[Us[\[Tau], \[Xi]], {\[Tau], 2}] - \[Delta]3*
      D[Us[\[Tau], \[Xi]], {\[Tau], 3}] - 
     I*\[Delta]4*D[Us[\[Tau], \[Xi]], {\[Tau], 4}] - 
     I*NS^2*Abs[Us[\[Tau], \[Xi]]]^2*Us[\[Tau], \[Xi]] == 0}; 
bc = {Us[\[Tau]max, \[Xi]] == 0, 
   Us[-\[Tau]max, \[Xi]] == 
    0, (D[Us[\[Tau], \[Xi]], {\[Tau], 1}] /. \[Tau] -> \[Tau]max) == 
    0, (D[Us[\[Tau], \[Xi]], {\[Tau], 1}] /. \[Tau] -> -\[Tau]max) == 
    0};
ic = {Us[\[Tau], 0] == Us1[\[Tau]]};
Print["seconds to obtain solution: ",
  time = AbsoluteTiming[
     Monitor[
       sol = 
        NDSolve[Join[eqs, ic, bc], 
         Us, {\[Tau], -\[Tau]max, \[Tau]max}, {\[Xi], 0, \[Xi]max}, 
         EvaluationMonitor :> (\[Xi]current = \[Xi]), 
         Method -> {"MethodOfLines", 
           "SpatialDiscretization" -> {"TensorProductGrid", 
             "MinPoints" -> 2000, "DifferenceOrder" -> 5}}(*,
         PrecisionGoal\[Rule]5,AccuracyGoal\[Rule]5,
         MaxSteps\[Rule]\[Infinity]*)], 
       "current \[Xi] (\!\(\*SubscriptBox[\(\[Xi]\), \(max\)]\)=" <> 
        ToString[\[Xi]max] <> "): " <> ToString[ \[Xi]current]];][[
    1]]] ;
Print["grid points along {\[Tau],\[Xi]}-directions: ", 
  Length /@ InterpolatingFunctionCoordinates[Us /. sol[[1]]]];
U2[\[Tau]_, \[Xi]_] = Us[\[Tau], \[Xi]] /. sol[[1]];
UAbs[\[Tau]_, \[Xi]_] = U2[\[Tau], \[Xi]] // Abs;
\[Tau]1 = -10.0; \[Tau]2 = 10.0; \[Xi]1 = 0.0; \[Xi]2 = \[Xi]max;
DensityPlot[
  UAbs[\[Tau], \[Xi]], {\[Tau], \[Tau]1, \[Tau]2}, {\[Xi], \[Xi]1, \
\[Xi]2}, PerformanceGoal -> "Quality", 
  ColorFunction -> "BlueGreenYellow", PlotRange -> All, 
  FrameLabel -> {"\[Tau]=T/\!\(\*SubscriptBox[\(T\), \(0\)]\)", 
    "\[Xi]=z/LD"}, PlotLabel -> "breathing of higher-order soliton", 
  MaxRecursion -> 4];
Plot3D[UAbs[\[Tau], \[Xi]], {\[Tau], \[Tau]1, \[Tau]2}, {\[Xi], \
\[Xi]1, \[Xi]2}, PerformanceGoal -> "Quality", 
  ColorFunction -> "BlueGreenYellow", PlotRange -> All, 
  AxesLabel -> {"\[Tau]=T/\!\(\*SubscriptBox[\(T\), \(0\)]\)", 
    "\[Xi]=z/LD", "amplitude"}, 
  PlotLabel -> "breathing of higher-order soliton", MaxRecursion -> 5];
GraphicsRow[{%%, %}, ImageSize -> 700]

Maybe it is suitable for your case. If not, it probably is a deep dive. Thank you very much for providing a target.

Best regards,

Tim

Hi Markus,

I modified the module so that you could select from the three cases you provided plus I added some multiples of the original $\delta$ parameters and pass in some additional options.

<< DifferentialEquations`InterpolatingFunctionAnatomy`

solitonMod[tmx_, xmx_, minpt_, casename_, plottitle_] := 
 Module[{a, tmax, xmax, d3, d4, NS, Us1, eqs, bc, ic,
   time, sol, U2, UAbs, t1, t2,
   x1, x2, dp, plt, grid},
  (* d3=0.00404040404040404;
  d4=-4.2087542087542085*^-6;*)
  d3 := 0 /; casename == "Base";
  d4 := 0 /; casename == "Base";
  d3 := 0.00404040404040404 /; casename == "Orig";
  d4 := -4.2087542087542085*^-6 /; casename == "Orig";
  d3 := 5 0.00404040404040404 /; casename == "Orig5x";
  d4 := 5*(-4.2087542087542085*^-6) /; casename == "Orig5x";
  d3 := 2 0.00404040404040404 /; casename == "Orig2x";
  d4 := 2*(-4.2087542087542085*^-6) /; casename == "Orig2x";
  d3 := 2.5 0.00404040404040404 /; casename == "Orig2.5x";
  d4 := 2.5*(-4.2087542087542085*^-6) /; casename == "Orig2.5x";
  d3 := 3.0 0.00404040404040404 /; casename == "Orig3x";
  d4 := 3.0*(-4.2087542087542085*^-6) /; casename == "Orig3x";
  d3 := 0.04 /; casename == "0.04";
  d4 := 0 /; casename == "0.04";
  NS = 4;

  xmax = Rationalize[xmx];
  tmax = Rationalize[tmx];
  a = 1.3862943611198906;

  Us1[t_] = Exp[-a*t^2];
  Plot[Us1[t], {t, -tmax, tmax}, Frame -> True, 
   PlotStyle -> Darker[Blue], PlotRange -> All, Filling -> Bottom];
  eqs = {D[Us[t, x] , x] - I/2*D[Us[t, x], {t, 2}] - 
      d3*D[Us[t, x], {t, 3}]
      - I*d4*D[Us[t, x], {t, 4}] - I*NS^2*Abs[Us[t, x]]^2*Us[t, x] == 
     0}; 
       bc = {Us[tmax, x] == Us1[tmax], 
    Us[-tmax, x] == 
     Us1[-tmax], (D[Us[t, x], {t, 1}] /. 
       t -> tmax) == (D[Us1[t], {t, 1}] /. 
       t -> tmax), (D[Us[t, x], {t, 1}] /. 
       t -> -tmax) == (D[Us1[t], {t, 1}] /. t -> -tmax)};
      ic = {Us[t, 0] == Us1[t]};
  Print["seconds to obtain solution: ",
   time = AbsoluteTiming[
      Monitor[
        sol = 
         NDSolve[Join[eqs, ic, bc], 
          Us, {t, -tmax, tmax}, {x, 0, xmax}, 
          EvaluationMonitor :> (xcurrent = x), 
          Method -> {"MethodOfLines", 
            "SpatialDiscretization" -> {"TensorProductGrid", 
              "MinPoints" -> minpt, "DifferenceOrder" -> 8}}(*,
          PrecisionGoal\[Rule]5,AccuracyGoal\[Rule]5*), 
          MaxSteps -> 10000, (*MaxStepFraction -> 1/600*)], 
        "current x (\!\(\*SubscriptBox[\(x\), \(max\)]\)=" <> 
         ToString[xmax] <> "): " <> ToString[ xcurrent]];][[1]]] ;
  Print["grid points along {t,x}-directions: ", 
   Length /@ InterpolatingFunctionCoordinates[Us /. sol[[1]]]];
  U2[t_, x_] = Us[t, x] /. sol[[1]];
  UAbs[t_, x_] = U2[t, x] // Abs;
  t1 = -10.0; t2 = 10.0; x1 = 0.0; x2 = xmax;
  dp = 1;
  plt = 1;
  grid = 1;
  dp = DensityPlot[UAbs[t, x], {t, t1, t2}, {x, x1, x2}, 
    PerformanceGoal -> "Quality", ColorFunction -> "BlueGreenYellow", 
    PlotRange -> All, FrameLabel -> {"t=T/T0", "x=z/LD"}, 
    PlotLabel -> plottitle, MaxRecursion -> 4];
  plt = Plot3D[UAbs[t, x], {t, t1, t2}, {x, x1, x2}, 
    PerformanceGoal -> "Quality", ColorFunction -> "BlueGreenYellow", 
    PlotRange -> All, AxesLabel -> {"t=T/T0", "x=z/LD", "amplitude"}, 
    PlotLabel -> plottitle, MaxRecursion -> 5, ImageSize -> Large];
  grid = GraphicsRow[{dp, plt}, ImageSize -> 700];
  {time, sol, dp, plt, grid}
  ]
Options[solitonfn] = {"tmax" -> 10, "xmax" -> 0.6, 
   "minpoints" -> 2100, "case" -> "Base", 
   "title" -> "breathing of higher-order soliton"};
solitonfn[OptionsPattern[]] := 
 solitonMod[OptionValue["tmax"], OptionValue["xmax"], 
  OptionValue["minpoints"], OptionValue["case"], OptionValue["title"]]

I ran some cursory tests and I did not see much effect of accuracy and precision goals, so I commented them out. Then, I ran a more complete series varying the MinPoints option of your three cases on two machines and the timing results are shown below (note that I shutdown and restarted Mathematica and saw some shifts but over all about the same failure rates). The columns are the $\delta=0$, Original Parameters, and $\delta_3=0.04$, respectively.

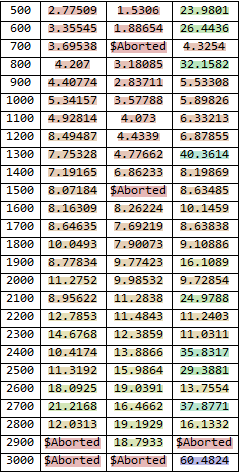
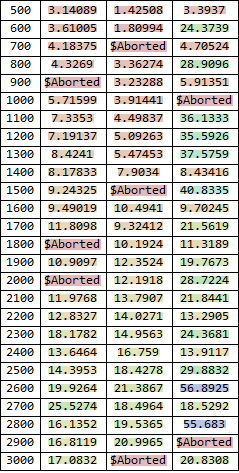
The mesh adaptation process is going to be somewhat random and in my experience are slow. We see that there is little change going from low MinPoints to high MinPoints indicating insensitivity.

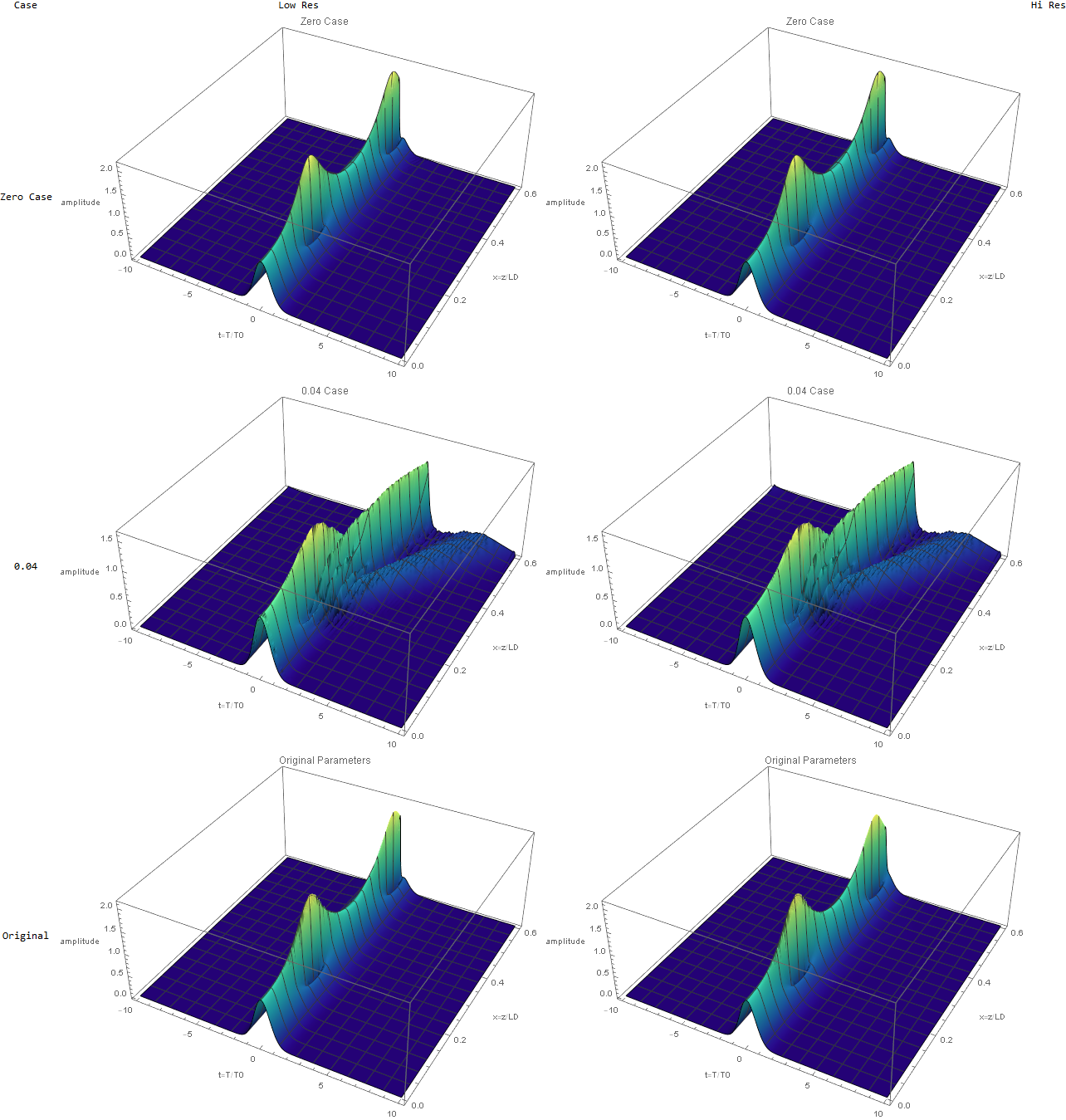
The original parameters seem to be stable and insensitive to MinPoints. Is there some some stability criterion for why they should be unstable? In any event, I ran a series to produce the animated gif below. At 2x the original parameters ( $\color{Red}{Red}$ curve), we start to see some ringing on the right tail. The ringing becomes more pronounced on the $\color{Purple}{Purple}$ curve at 2.5x original and you can see a fast moving shallow wave propagate to the right. At 3x, it is slower but higher amplitude.

hires0 = solitonfn["minpoints" -> 2800, "title" -> "Zero Case"];
hiresOrig = 
  solitonfn["case" -> "Orig", "minpoints" -> 2800, 
   "title" -> "Original Parameters"];
hiresOrig2x = 
  solitonfn["case" -> "Orig2x", "minpoints" -> 2900, 
   "title" -> "2x Original Parameters"];
hiresOrig25x = 
  solitonfn["case" -> "Orig2.5x", "minpoints" -> 2900, 
   "title" -> "2.5x Original Parameters"];
hiresOrig3x = 
  solitonfn["case" -> "Orig3x", "minpoints" -> 2900, 
   "title" -> "3x Original Parameters"];
hiresOrig5x = 
  solitonfn["case" -> "Orig5x", "minpoints" -> 2800, 
   "title" -> "5x Original Parameters"];
hires04 =  
  solitonfn["case" -> "0.04", "minpoints" -> 2800, 
   "title" -> "0.04 Case"];


f = ((#1 - #2)/(#3 - #2)) &;   
pltsComb = 
  Monitor[Table[
    Plot[{Evaluate[Abs[Us[\[Tau], i]] /. Last[hires0[[2]]]], 
      Evaluate[Abs[Us[\[Tau], i]] /. Last[hires04[[2]]]], 
      Evaluate[Abs[Us[\[Tau], i]] /. Last[hiresOrig[[2]]]], 
      Evaluate[Abs[Us[\[Tau], i]] /. Last[hiresOrig2x[[2]]]], 
      Evaluate[Abs[Us[\[Tau], i]] /. Last[hiresOrig25x[[2]]]], 
      Evaluate[Abs[Us[\[Tau], i]] /. Last[hiresOrig3x[[2]]]], 
      Evaluate[
       Abs[Us[\[Tau], i]] /. Last[hiresOrig5x[[2]]]]}, {\[Tau], -4, 
      8}, PlotRange -> {0, 2.25}, ImageSize -> Large, 
     PlotStyle -> Thick, 
     PlotLegends -> 
      Placed[LineLegend[{"Zero", 
         "\!\(\*SubscriptBox[\(\[Delta]\), \(3\)]\)=0.04", "Original",
          "Original2x", "Original2.5x", "Original3x", "Original5x"}, 
        LegendFunction -> Frame], {0.75, 0.75}]], {i, 0, 0.6, 0.003}],
    Grid[{{"Total progress:", 
      ProgressIndicator[
       Dynamic[f[i, 0, 0.6, 0.003]]]}, {"i=", {Dynamic@i}}}]];

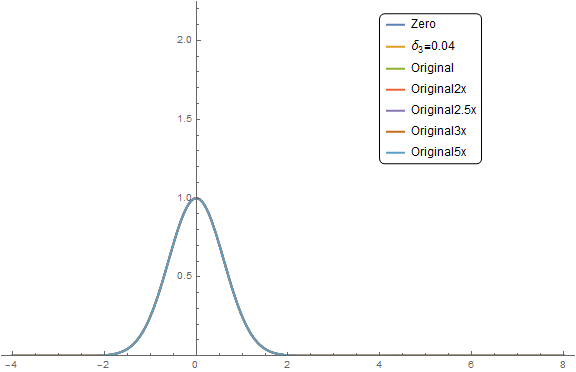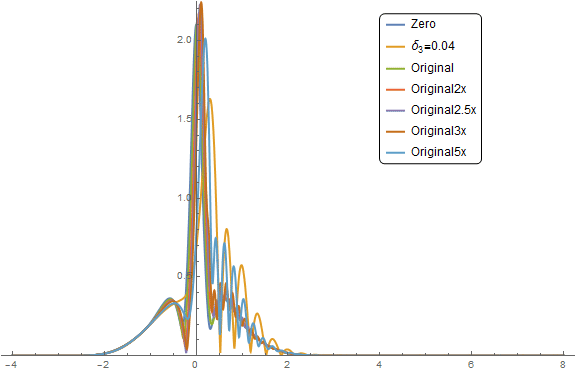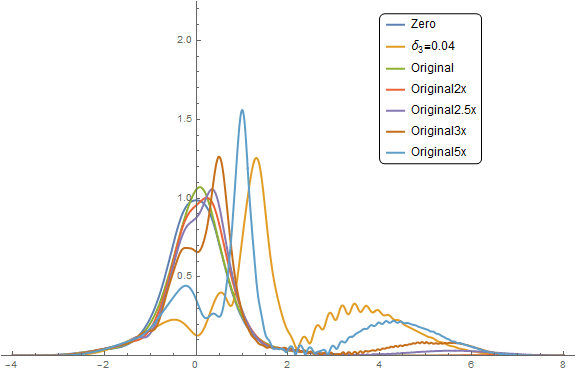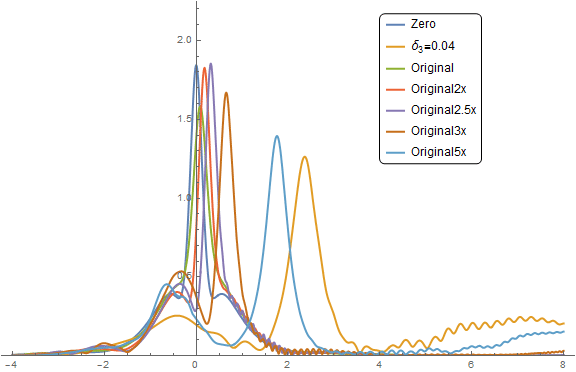
The module seems to be behaving in consistent way and will solve in less than 10 seconds for many cases. At the current solver settings, the simulation hangs about 20% of the time in a random fashion. Now, the Test Analyze and Fix phase kicks in.

Hi Markus,

There are many potential ways to deal with this issue. In an ideal world, you would provide robust simulation settings and it would solve in a predictable way. Generally, it can take 100s to 1000s of simulations to find optimal and robust simulation settings. Alternatively, you could try less glamorous approaches such as detection, preemption, and restarting the simulation. For example, you could use wrap the process in while loop and use the TimeConstrained function to stop crawling simulations and restart them with another MinPoints value. Of course, you don't want to stop a bunch of simulations that are about to finish, so you need a good balking time. While the process is autonomously running in the background at 80%, you can be investigating better approaches, but at least you are getting some work done.

The mesh is always adapting, it is just that it sometime gets confused. What would be ideal is if we could supply a pre-refined non-uniform mesh as an initial starting point like we do with the FEM technique. We would have a fine mesh in the center and coarser mesh in the wings. Then the solver as an initial guess for refinement. Solvers work best when supplied with good initial guesses. I don't think this is an option with the Numerical Method of Lines.

Also, I zoomed in to get a better look at the "fission". You might want take a look to verify that it is behaving physically.

Finally, I added $Sech^2$ option for a pulse. It should not underflow like the Gaussian at large absolute time. I tested it out on $x=1.8$ and $\tau_{max}=20$ for the original case. You can see some "fission" taking place where it did not appear to full develop in the shorter domain.

Short Domain

Bigger Domain

I hope that we are in better region than when we started.

Best regards,

Tim

Attachments:

solitonModuleForMarkus.nb

An error occurs when calculating the function Us1[\[Tau]]. The interval {\[Tau], -\[Tau]max, \[Tau]max} is selected too large. It is necessary to reduce the interval by an order of magnitude, to set the agreed boundary conditions and improve the accuracy of calculations, to choose the correct method. Then we have a solution to the equation

\[Delta]3 = 0.00404040404040404`30;
\[Delta]4 = -4.2087542087542085`30*^-6;
NS = 4.483404754211932`30;
NS2 = 20.100918190090154388694371172624`30;
\[Xi]max = 1;
\[Tau]max = 3;
q = 1.3862943611198906`30;
Us1[\[Tau]_] = Exp[-q*\[Tau]^2];
Plot[Us1[\[Tau]], {\[Tau], -\[Tau]max, \[Tau]max}, Frame -> True, 
 PlotStyle -> Darker[Blue], PlotRange -> All, Filling -> Bottom]
eqs = {D[Us[\[Tau], \[Xi]] , \[Xi]] - 
     I/2*D[Us[\[Tau], \[Xi]], {\[Tau], 2}] - \[Delta]3*
      D[Us[\[Tau], \[Xi]], {\[Tau], 3}] - 
     I*\[Delta]4*D[Us[\[Tau], \[Xi]], {\[Tau], 4}] - 
     I*NS2*Abs[Us[\[Tau], \[Xi]]]^2*Us[\[Tau], \[Xi]] == 0}; 
bc = {Us[\[Tau]max, \[Xi]] == Us1[\[Tau]max], 
   Us[-\[Tau]max, \[Xi]] == 
    Us1[-\[Tau]max], (D[
       Us[\[Tau], \[Xi]], {\[Tau], 1}] /. \[Tau] -> \[Tau]max) == (D[
       Us1[\[Tau]], {\[Tau], 1}] /. \[Tau] -> \[Tau]max), (D[
       Us[\[Tau], \[Xi]], {\[Tau], 1}] /. \[Tau] -> -\[Tau]max) == (D[
       Us1[\[Tau]], {\[Tau], 1}] /. \[Tau] -> -\[Tau]max)};
ic = {Us[\[Tau], 0] == Us1[\[Tau]]};


sol = NDSolve[Join[eqs, ic, bc], 
   Us, {\[Tau], -\[Tau]max, \[Tau]max}, {\[Xi], 0, \[Xi]max}, 
   Method -> {"MethodOfLines", 
     "SpatialDiscretization" -> {"TensorProductGrid", 
       "MinPoints" -> 40, "MaxPoints" -> 100, 
       "DifferenceOrder" -> "Pseudospectral"}}, MaxSteps -> 10^6, 
   WorkingPrecision -> 20] // AbsoluteTiming
Plot3D[Abs[Us[\[Tau], \[Xi]]] /. 
  Last[sol], {\[Tau], -\[Tau]max, \[Tau]max}, {\[Xi], 0, \[Xi]max}, 
 Mesh -> None, ColorFunction -> Hue, PlotRange -> All]

I offered you a working code for solving your problem. You can change the parameters to calculate faster, for example, lower the accuracy of the calculations, setting "MaxPoints" -> 80`andWorkingPrecision -> 15`.

Thank you for the help. May I ask what kind of code you have used to solve the nonlinear Schroedinger equation? Did that include dispersion? May I see your code? Best, Markus