Open in Cloud | Click on Map to ZOOM | Download to Desktop via Attachments Below

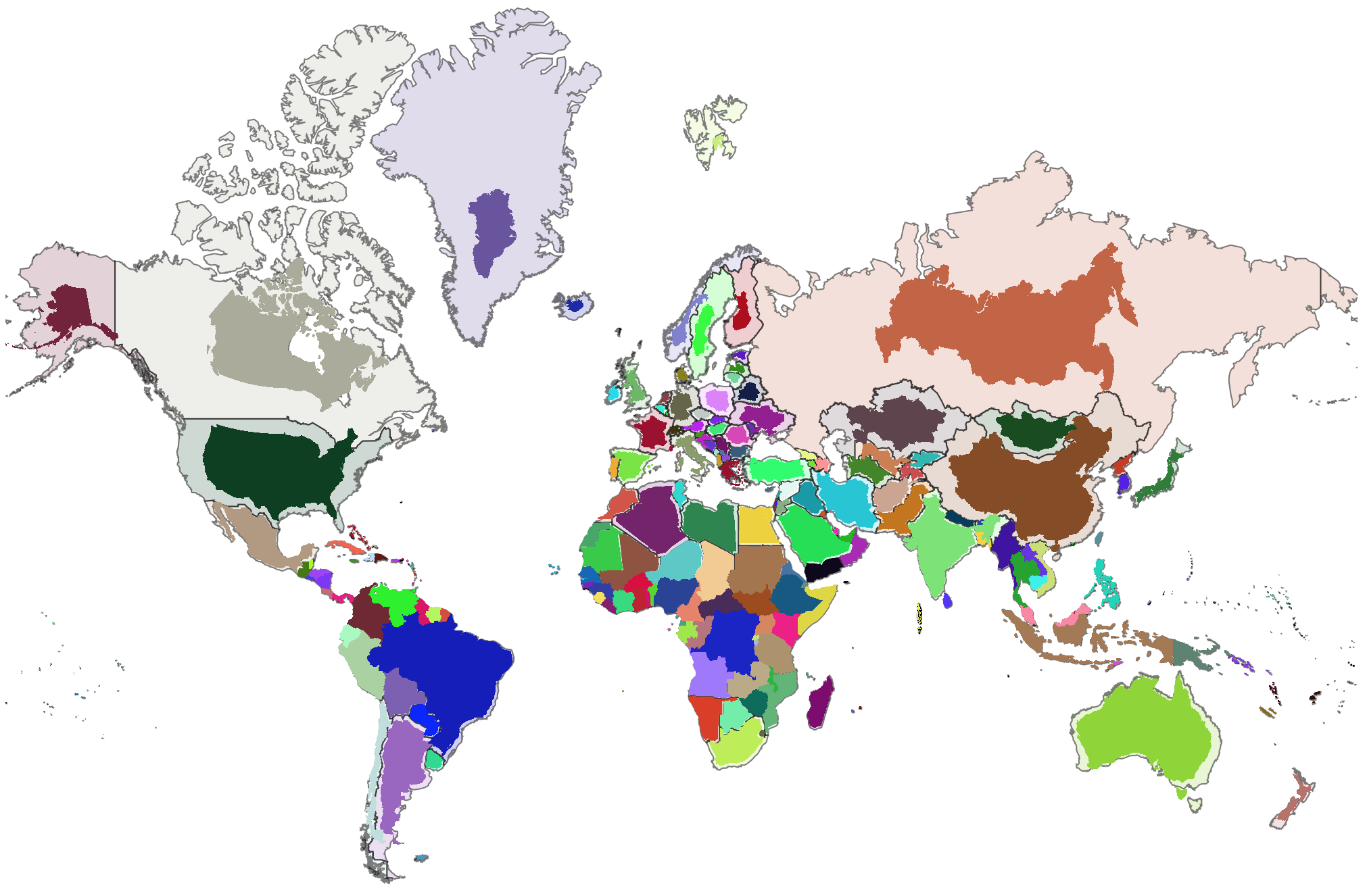
Here are two simple ways of constructing Mercator maps of the world that show the large distortion in size for countries far from the equator.

Take all countries polygons and central positions, considering Alaska as a separate case:

countries = Append[CountryData[], Entity["AdministrativeDivision", {"Alaska", "UnitedStates"}]];
polygons = EntityValue[countries, "Polygon"];
positions = EntityValue[countries, "Position"];

Project those positions with the Mercator projection, and extract the {x, y} values ("Data" is one of many geo extractors of data added in version 12, here effectively equivalent to using First):

projectedpositions = GeoGridPosition[GeoPosition[positions], "Mercator"]["Data"];

For later use, select a random color for each country:

colors = RandomColor[Length[countries]];

First method

Project the polygons with an equal-area projection, in this case "LambertAzimuthal", using the same reference model of the "Mercator" projection, which is 180/Pi (this value is chosen so that the horizontal axis of Mercator maps is in degrees). Center the projections at the country center, and then move the result back to the Mercator coordinates for that center:

projections = MapThread[
    {"LambertAzimuthal", "Centering" -> #1, "GridOrigin" -> #2, "ReferenceModel" -> 180/Pi} &, 
    {positions, projectedpositions}
];

projectedpolygons = MapThread[GeoGridPosition, {polygons, projections}] /. GeoGridPosition[data_, proj_] :> data;

The main idea is to remove the GeoGridPosition heads from the result. This will tell GeoGraphics that the result should not be touched. If we didn't do this, GeoGraphics would undo the Lambert-Azimuthal projection.

GeoGraphics[{
    EdgeForm[Opacity[0.5, Black]], Transpose[{colors, polygons}],
    GeoStyling[Opacity[1]], EdgeForm[], Transpose[{colors, projectedpolygons}]
},
    GeoProjection -> "Mercator", ImageSize -> 1000, GeoBackground -> None, 
    GeoCenter -> 10, GeoGridRange -> {{-170, 190}, {-90, 180}}
]

This shows, for each country, the highly distorted polygon as it appears in the Mercator projection, and another version with a much more faithful representation of size and shape, but displaced.

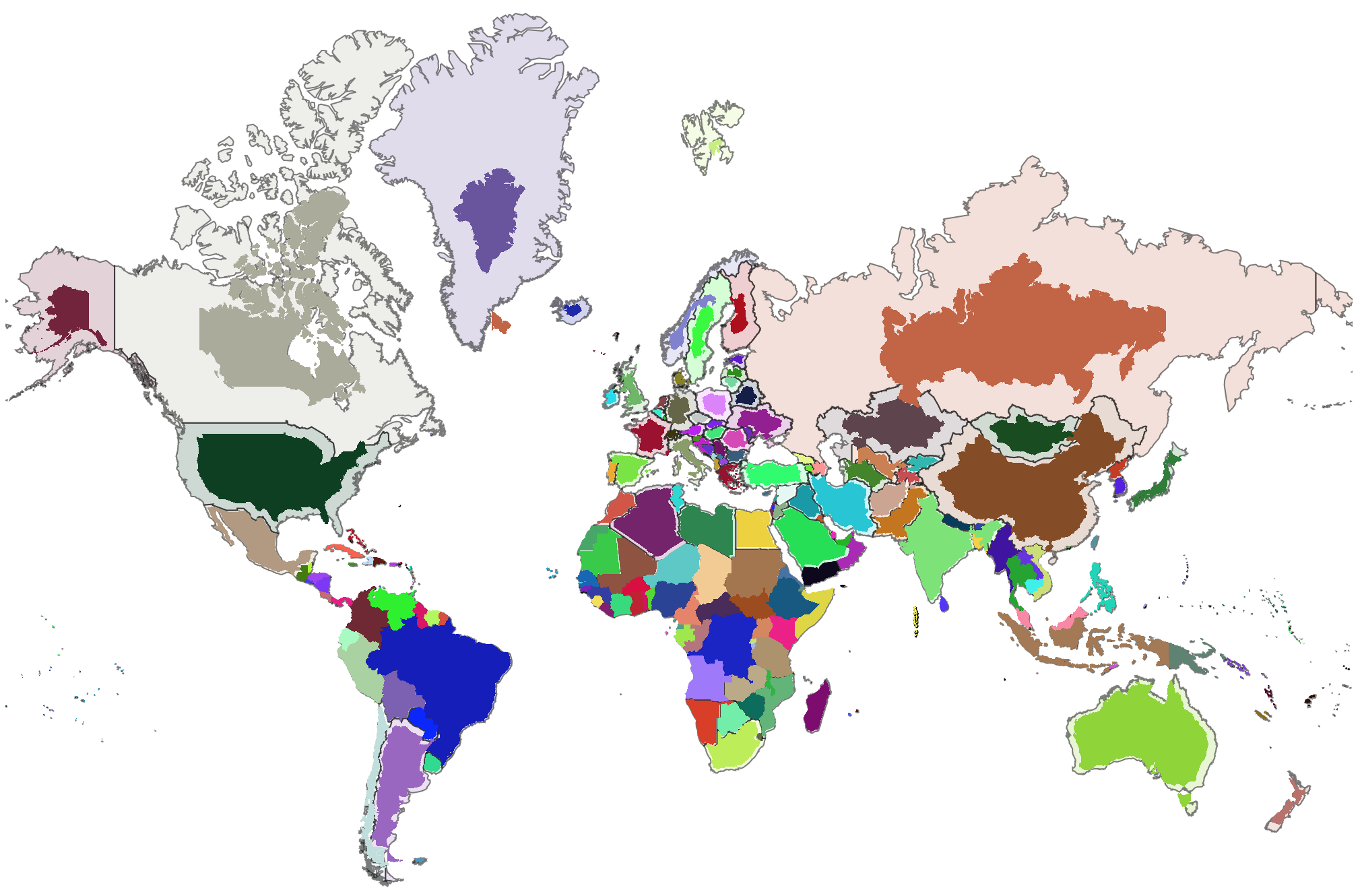
Second method (an approximation)

Here we also use the Mercator projection, so the shapes coincide, but we rescale the polygons using the new-in-12 function GeoGridUnitDistance, which reports projection distortion for a given projection at a given location (also in a given direction, but Mercator is conformal, so distortion is independent of direction, and we choose direction 0). This method is just an approximation, because we are using the distortion factor at a single point of the country, while distortion varies.

factors = GeoGridUnitDistance["Mercator", positions, 0] / GeoGridUnitDistance["Mercator", GeoPosition[{0, 0}], 0];

projections = MapThread[
    {"Mercator", "Centering" -> #1, "GridOrigin" -> #2 {1, 1 - #3}, "CentralScaleFactor" -> #3} &,
    {positions, projectedpositions, factors}
];

These last two inputs are identical to what we had before:

projectedpolygons = MapThread[GeoGridPosition, {polygons, projections}] /. GeoGridPosition[data_, proj_] :> data;

GeoGraphics[{
    EdgeForm[Opacity[0.5, Black]], Transpose[{colors, polygons}],
    GeoStyling[Opacity[1]], EdgeForm[], Transpose[{colors, projectedpolygons}]
},
    GeoProjection -> "Mercator", ImageSize -> 1000, GeoBackground -> None, 
    GeoCenter -> 10, GeoGridRange -> {{-170, 190}, {-90, 180}}
]

Attachments:

Comparison-of-Co...nb