Message Boards Message Boards

Have Random Integers by the Number of Digits and through Real Numbers

In this work I show how to generate random integers by the number of their digits, how to generate random integers with their number of each digit locked in mean value and how to generate random integers guided by a real number either by the beginning of the number or by a random part of the same.

The topics here are divided into:

  • A)Random Integers generated by the Number of Digits

  • B)Random Integer with seed generated by the number of digits

  • C)Random Integer Generation with locked digits.

  • D)Generation of Random Integer through real numbers (from the beginning of the number)

  • E)Generation of Random Integer through real numbers (randomly choosing the position in the number, band)

  • F)Use of large sampling through randomly efficient candidates.

A)Random integers generated by the number of digits

With the codes below we can modify the RandomInteger function to generate an integer number with the desired number of digits (dig).

dig = 100;

gen = RandomInteger[9, dig];

Text[Style[gen, Small, Purple]]

fe = If[FromDigits[Take[gen, 1]] > 0.5, gen, RandomInteger[9, dig]];

ff = If[FromDigits[Take[fe, 1]] > 0.5, fe, RandomInteger[9, dig]];

fg = If[FromDigits[Take[ff, 1]] > 0.5, ff, RandomInteger[9, dig]];

fh = If[FromDigits[Take[fg, 1]] > 0.5, fg, RandomInteger[9, dig]];

fi = If[FromDigits[Take[fh, 1]] > 0.5, fh, RandomInteger[9, dig]];

Text[Style[FromDigits[fi], Medium, Bold, Blue]]





Grid[{{"dig 1", "dig 2", "dig 3", "dig 4", "dig 5", "dig 6", "dig 7", 

   "dig 8", "dig 9", "dig 0"}, DigitCount[FromDigits[fi]]}, 

 Frame -> All, Background -> {None, {{LightBlue, LightRed}}}]



Table[BarChart[DigitCount[FromDigits[fi]], 

  ChartElementFunction -> "GlassRectangle", ChartStyle -> "Pastel", 

  ChartLabels -> {"1", "2", "3", "4", "5", "6", "7", "8", "9", "0"}, 

  LabelingFunction -> p, PlotLabel -> p, Ticks -> Automatic, 

  LabelingSize -> 30], {p, {"Digit Count"}}]



ListPlot[fi, PlotRange -> {{0, dig + 1}, {-1, 10}}, 

 PlotStyle -> PointSize[Medium], PlotTheme -> "Scientific", 

 GridLines -> Automatic, Ticks -> Automatic]

This example above was with 100 digits giving the following result (containing rate of doubles, etc - visualization and in ALL cases in this work we can interpret each separate digit as a sample or as an integer formed by the digits):

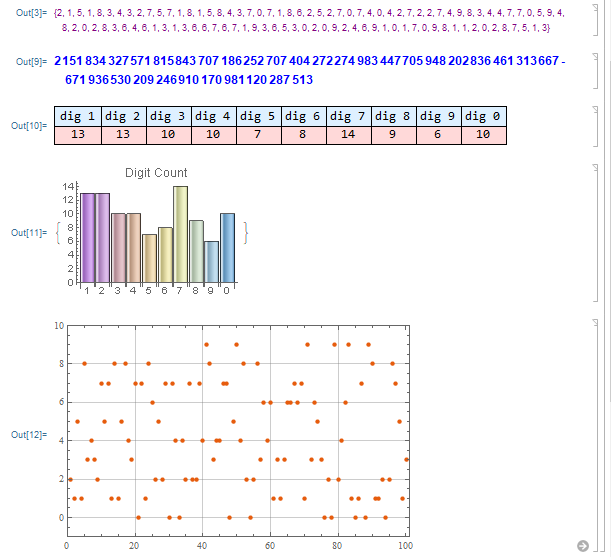
enter image description here

The loops in the code were executed simply with the “If” command, there are 6 loops and each loop decreases the chance of a result error by a factor of 10, that is, the result will only have a different number of digits than was required in the probability from 1 to 10^6.

Of course we can manipulate any of the results using Partition and StringPartition to get multiple samples at once with a new number of digits (di) with the following example:

kf = {9, 0, 5, 7, 1, 3, 3, 4, 0, 3, 2, 5, 3, 8, 4, 7, 0, 2, 7, 8, 6, 

  2, 9, 8, 5, 2, 2, 5, 1, 8, 6, 5, 7, 3, 5, 2, 9, 3, 0, 0, 2, 5, 3, 6,

   1, 7, 4, 4, 4, 9, 2, 9, 5, 1, 0, 2, 7, 4, 3, 0, 5, 0, 3, 3, 6, 8, 

  1, 4, 2, 1, 5, 5, 2, 3, 2, 4, 2, 4, 6, 6, 2, 4, 3, 5, 4, 6, 0, 8, 6,

   8, 6, 8, 5, 0, 4, 6, 0, 0, 8, 6}

di = 10

Partition[kf, di]

zz = ToString[FromDigits[kf], InputForm]

StringPartition[zz, di]

Coming from the example code above, the initial result of 100 digits was grouped into 10 numbers with 10 digits:

enter image description here

B)Random seeds generated by the number of digits

Similarly, the SeedRandom command was adapted to generate integer random numbers with a specific number of digits. The code is as follows:

dig = 10;
gen = BlockRandom[SeedRandom[12345]; RandomInteger[9, dig]];
Text[Style[gen, Small, Purple]]
k = If[FromDigits[Take[gen, 1]] > 0.5, FromDigits[gen], "CHANGE SEED"];
If[k == "CHANGE SEED", Text[Style["CHANGE SEED", Large, Red]], 
 Text[Style[k, Medium, Bold, Blue]]]

If[k == "CHANGE SEED", Text[Style["CHANGE SEED", Large, Red]], 
 Grid[{{"dig 1", "dig 2", "dig 3", "dig 4", "dig 5", "dig 6", "dig 7",
     "dig 8", "dig 9", "dig 0"}, DigitCount[FromDigits[gen]]}, 
  Frame -> All, Background -> {None, {{LightBlue, LightRed}}}]]

If[k == "CHANGE SEED", Text[Style["CHANGE SEED", Large, Red]], 
 Table[BarChart[DigitCount[FromDigits[gen]], 
   ChartElementFunction -> "GlassRectangle", ChartStyle -> "Pastel", 
   ChartLabels -> {"1", "2", "3", "4", "5", "6", "7", "8", "9", "0"}, 
   LabelingFunction -> p, PlotLabel -> p, Ticks -> Automatic, 
   LabelingSize -> 30], {p, {"Digit Count"}}]]

If[k == "CHANGE SEED", Text[Style["CHANGE SEED", Large, Red]], 
 ListPlot[gen, PlotRange -> {{0, dig + 1}, {-1, 10}}, 
  PlotStyle -> PointSize[Medium], PlotTheme -> "Scientific", 
  GridLines -> Automatic, Ticks -> Automatic]]

Giving the following result:

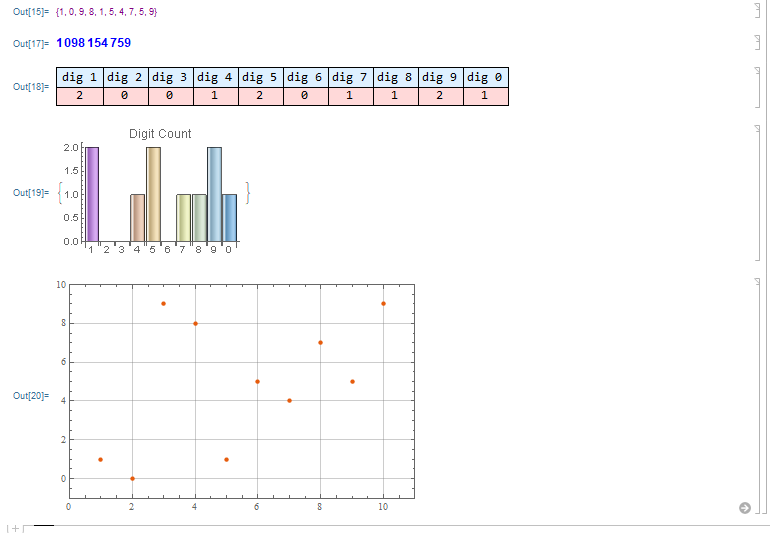
enter image description here

The code says if the chosen seed cannot generate the required number of digits because it will always give the same result depending on the seed:

enter image description here

C) Random Integer Generation with locked digits

With the code below we can randomly generate integer numbers by the number of digits desired, forcing to lock the number of digits of each type in a balanced way, practically extinguishing the deviations (except for the ratio of double, triple, etc.).

dig = 100;
gen = RandomSample[
   IntegerDigits[IntegerPart[(10^dig)*1234567890/9999999999]]];
fe = If[FromDigits[Take[gen, 1]] > 0.5, gen, 
   RandomSample[
    IntegerDigits[IntegerPart[(10^dig)*1234567890/9999999999]]]];
ff = If[FromDigits[Take[fe, 1]] > 0.5, fe, 
   RandomSample[
    IntegerDigits[IntegerPart[(10^dig)*1234567890/9999999999]]]];
fg = If[FromDigits[Take[ff, 1]] > 0.5, ff, 
   RandomSample[
    IntegerDigits[IntegerPart[(10^dig)*1234567890/9999999999]]]];
fh = If[FromDigits[Take[fg, 1]] > 0.5, fg, 
   RandomSample[
    IntegerDigits[IntegerPart[(10^dig)*1234567890/9999999999]]]];
fi = If[FromDigits[Take[fh, 1]] > 0.5, fh, 
   RandomSample[
    IntegerDigits[IntegerPart[(10^dig)*1234567890/9999999999]]]];
Text[Style[fi, Small, Purple]]
Text[Style[FromDigits[fi], Medium, Bold, Blue]]

Grid[{{"dig 1", "dig 2", "dig 3", "dig 4", "dig 5", "dig 6", "dig 7", 
   "dig 8", "dig 9", "dig 0"}, DigitCount[FromDigits[fi]]}, 
 Frame -> All, Background -> {None, {{Yellow, LightPurple}}}]

ListLinePlot[DigitCount[FromDigits[fi]], Filling -> Axis, 
 PlotRange -> All, PlotTheme -> "Scientific", PlotStyle -> Purple, 
 PlotMarkers -> {Automatic, 10}]

ListPlot[fi, PlotRange -> {{0, dig + 1}, {-1, 10}}, 
 PlotStyle -> PointSize[Medium], PlotTheme -> "Scientific", 
 GridLines -> Automatic, Ticks -> Automatic]

Giving the following result:

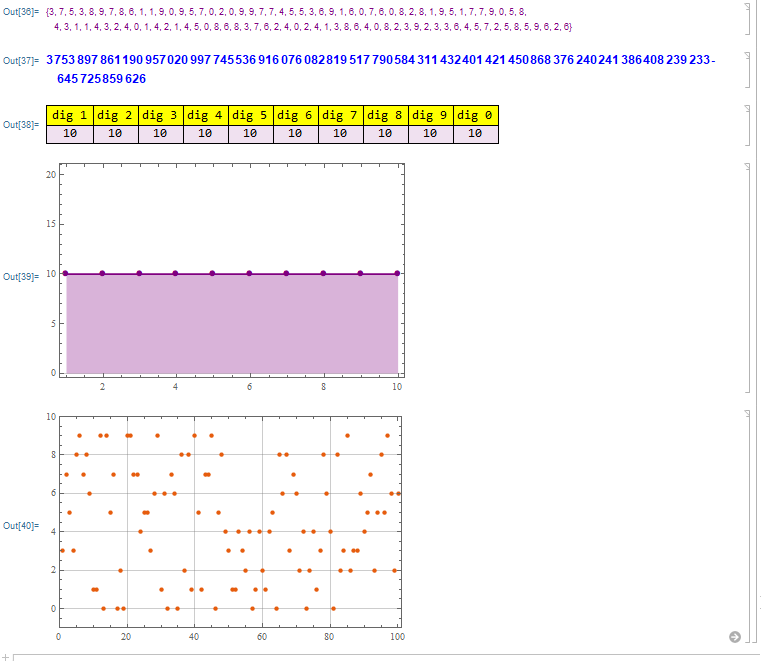
enter image description here

This form of generation simulates large samplings (unrealistically large), but very efficient for results where it is sought to eliminate deviations from the arithmetical mean, digit count, deviation in the coin toss.

D) Random Integer Generation through Real Numbers

-(from the beginning of the number)

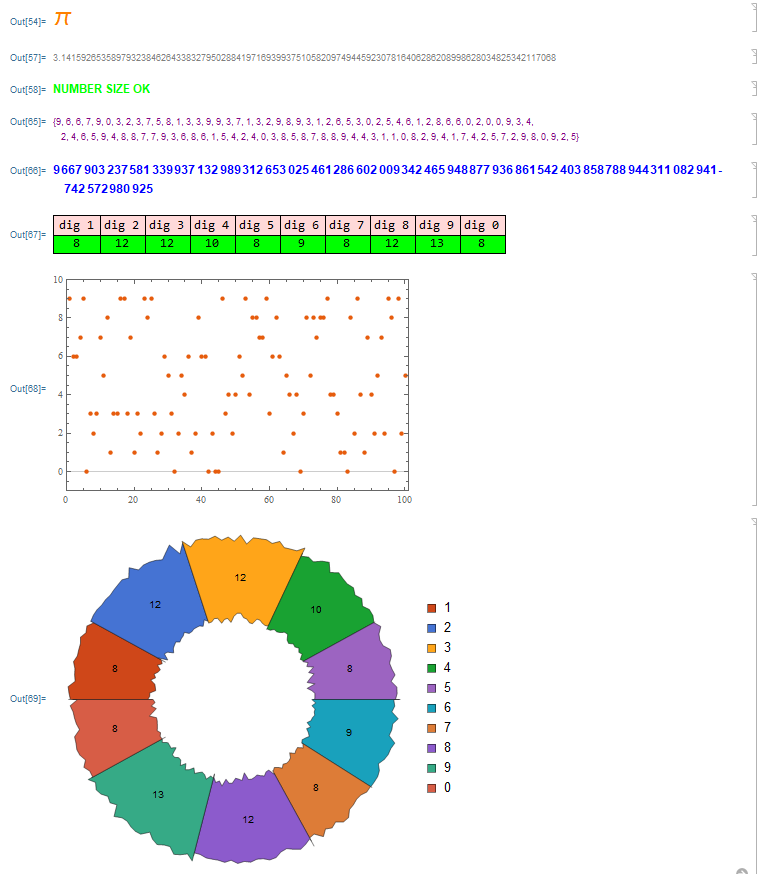
The sample where the random permutation will be performed comes from a real number chosen as a guide (num) and its digits will be the same as the number chosen, only randomly permuted. The example below was chosen Pi and a 30-digit random sample was required.

enter image description here

The code for doing this (with 100 digits in the example below) was done as follows:

(You can use ANY Real Number between 1000 and 0.001 by this code´s limit)

The code is:

num = Pi;
Text[Style[num, Large, Orange]]
dig = 100;
nn = Abs[N[num, dig]];
Text[Style[nn, Small, Gray]]
hh = If[0.001 < nn < 1000, 
  Text[Style["NUMBER SIZE OK", Medium, Bold, Green]], 
  Text[Style["CHANGE NUMBER SIZE", Large, Bold, Red]]]
gen = RandomSample[
   IntegerDigits[
    If[100 < IntegerPart[nn*10^dig]/10^dig < 1000, 
     IntegerPart[nn*10^(dig - 3)], 
     If[10 < IntegerPart[nn*10^dig]/10^dig < 100, 
      IntegerPart[nn*10^(dig - 2)], 
      If[0.1 < IntegerPart[nn*10^dig]/10^dig < 1, 
       IntegerPart[nn*10^dig], 
       If[IntegerPart[nn*10^dig]/10^dig > 1, 
        IntegerPart[nn*10^(dig - 1)], 
        If[0.01 < IntegerPart[nn*10^dig]/10^dig < 0.1, 
         IntegerPart[nn*10^(dig + 1)], 
         IntegerPart[nn*10^(dig + 2)]]]]]]]];
fe = If[FromDigits[Take[gen, 1]] > 0.5, gen, 
   RandomSample[
    IntegerDigits[
     If[100 < IntegerPart[nn*10^dig]/10^dig < 1000, 
      IntegerPart[nn*10^(dig - 3)], 
      If[10 < IntegerPart[nn*10^dig]/10^dig < 100, 
       IntegerPart[nn*10^(dig - 2)], 
       If[0.1 < IntegerPart[nn*10^dig]/10^dig < 1, 
        IntegerPart[nn*10^dig], 
        If[IntegerPart[nn*10^dig]/10^dig > 1, 
         IntegerPart[nn*10^(dig - 1)], 
         If[0.01 < IntegerPart[nn*10^dig]/10^dig < 0.1, 
          IntegerPart[nn*10^(dig + 1)], 
          IntegerPart[nn*10^(dig + 2)]]]]]]]]];
ff = If[FromDigits[Take[fe, 1]] > 0.5, fe, 
   RandomSample[
    IntegerDigits[
     If[100 < IntegerPart[nn*10^dig]/10^dig < 1000, 
      IntegerPart[nn*10^(dig - 3)], 
      If[10 < IntegerPart[nn*10^dig]/10^dig < 100, 
       IntegerPart[nn*10^(dig - 2)], 
       If[0.1 < IntegerPart[nn*10^dig]/10^dig < 1, 
        IntegerPart[nn*10^dig], 
        If[IntegerPart[nn*10^dig]/10^dig > 1, 
         IntegerPart[nn*10^(dig - 1)], 
         If[0.01 < IntegerPart[nn*10^dig]/10^dig < 0.1, 
          IntegerPart[nn*10^(dig + 1)], 
          IntegerPart[nn*10^(dig + 2)]]]]]]]]];
fg = If[FromDigits[Take[ff, 1]] > 0.5, ff, 
   RandomSample[
    IntegerDigits[
     If[100 < IntegerPart[nn*10^dig]/10^dig < 1000, 
      IntegerPart[nn*10^(dig - 3)], 
      If[10 < IntegerPart[nn*10^dig]/10^dig < 100, 
       IntegerPart[nn*10^(dig - 2)], 
       If[0.1 < IntegerPart[nn*10^dig]/10^dig < 1, 
        IntegerPart[nn*10^dig], 
        If[IntegerPart[nn*10^dig]/10^dig > 1, 
         IntegerPart[nn*10^(dig - 1)], 
         If[0.01 < IntegerPart[nn*10^dig]/10^dig < 0.1, 
          IntegerPart[nn*10^(dig + 1)], 
          IntegerPart[nn*10^(dig + 2)]]]]]]]]];
fh = If[FromDigits[Take[fg, 1]] > 0.5, fg, 
   RandomSample[
    IntegerDigits[
     If[100 < IntegerPart[nn*10^dig]/10^dig < 1000, 
      IntegerPart[nn*10^(dig - 3)], 
      If[10 < IntegerPart[nn*10^dig]/10^dig < 100, 
       IntegerPart[nn*10^(dig - 2)], 
       If[0.1 < IntegerPart[nn*10^dig]/10^dig < 1, 
        IntegerPart[nn*10^dig], 
        If[IntegerPart[nn*10^dig]/10^dig > 1, 
         IntegerPart[nn*10^(dig - 1)], 
         If[0.01 < IntegerPart[nn*10^dig]/10^dig < 0.1, 
          IntegerPart[nn*10^(dig + 1)], 
          IntegerPart[nn*10^(dig + 2)]]]]]]]]];
fi = If[FromDigits[Take[fh, 1]] > 0.5, fh, 
   RandomSample[
    IntegerDigits[
     If[100 < IntegerPart[nn*10^dig]/10^dig < 1000, 
      IntegerPart[nn*10^(dig - 3)], 
      If[10 < IntegerPart[nn*10^dig]/10^dig < 100, 
       IntegerPart[nn*10^(dig - 2)], 
       If[0.1 < IntegerPart[nn*10^dig]/10^dig < 1, 
        IntegerPart[nn*10^dig], 
        If[IntegerPart[nn*10^dig]/10^dig > 1, 
         IntegerPart[nn*10^(dig - 1)], 
         If[0.01 < IntegerPart[nn*10^dig]/10^dig < 0.1, 
          IntegerPart[nn*10^(dig + 1)], 
          IntegerPart[nn*10^(dig + 2)]]]]]]]]];
Text[Style[fi, Small, Purple]]
Text[Style[FromDigits[fi], Medium, Bold, Blue]]

Grid[{{"dig 1", "dig 2", "dig 3", "dig 4", "dig 5", "dig 6", "dig 7", 
   "dig 8", "dig 9", "dig 0"}, DigitCount[FromDigits[fi]]}, 
 Frame -> All, Background -> {None, {{LightRed, Green}}}]

ListPlot[fi, PlotRange -> {{0, dig + 1}, {-1, 10}}, 
 PlotStyle -> PointSize[Medium], PlotTheme -> "Scientific", 
 Ticks -> Automatic]

PieChart[{DigitCount[FromDigits[fi]]}, SectorOrigin -> {Automatic, 1},
  PlotTheme -> {"BoldScheme", "VibrantColor"}, 
 ChartElementFunction -> "NoiseSector", 
 ChartLabels -> {DigitCount[FromDigits[fi]]}, 
 ChartLegends -> {"1", "2", "3", "4", "5", "6", "7", "8", "9", "0"}]

Which gives the following result (plus an alternate view of PieChart with NoiseSector to represent the number of digits):

enter image description here

E) Random Integer Generation through Real Numbers

-(randomly choosing the starting position in the number - band)

In the example below, the Pi number was chosen to be the digit guide and a random 30-digit integer was required using the same digits of a randomly chosen portion of the guide number.

enter image description here

Similarly we can choose any real number between 1000 and 0.001 to be the guide number (num).

The number of digits required is the value "ddd". The code is set to choose a sample within a set of 10^5 digits as determined in the "dig" value, and can be changed to a larger value that supports sampling if so required.

num = Pi;
Text[Style[num, Large, Orange]]
ddd = 1000;
Text[Style[ddd, Medium, Pink]]
dig = 100000;
nn = Abs[N[num, dig]];
div = Divisors[ddd];
hh = If[0.001 < nn < 1000, 
  Text[Style["NUMBER SIZE OK", Medium, Bold, Green]], 
  Text[Style["CHANGE NUMBER SIZE", Large, Bold, Red]]]
gen = RandomSample[
  IntegerDigits[
   If[100 < IntegerPart[nn*10^dig]/10^dig < 1000, 
    IntegerPart[nn*10^(dig - 3)], 
    If[10 < IntegerPart[nn*10^dig]/10^dig < 100, 
     IntegerPart[nn*10^(dig - 2)], 
     If[0.1 < IntegerPart[nn*10^dig]/10^dig < 1, 
      IntegerPart[nn*10^dig], 
      If[IntegerPart[nn*10^dig]/10^dig > 1, 
       IntegerPart[nn*10^(dig - 1)], 
       If[0.01 < IntegerPart[nn*10^dig]/10^dig < 0.1, 
        IntegerPart[nn*10^(dig + 1)], 
        IntegerPart[nn*10^(dig + 2)]]]]]]]]; fe = 
 If[FromDigits[Take[gen, 1]] > 0.5, gen, 
  RandomSample[
   IntegerDigits[
    If[100 < IntegerPart[nn*10^dig]/10^dig < 1000, 
     IntegerPart[nn*10^(dig - 3)], 
     If[10 < IntegerPart[nn*10^dig]/10^dig < 100, 
      IntegerPart[nn*10^(dig - 2)], 
      If[0.1 < IntegerPart[nn*10^dig]/10^dig < 1, 
       IntegerPart[nn*10^dig], 
       If[IntegerPart[nn*10^dig]/10^dig > 1, 
        IntegerPart[nn*10^(dig - 1)], 
        If[0.01 < IntegerPart[nn*10^dig]/10^dig < 0.1, 
         IntegerPart[nn*10^(dig + 1)], 
         IntegerPart[nn*10^(dig + 2)]]]]]]]]]; ff = 
 If[FromDigits[Take[fe, 1]] > 0.5, fe, 
  RandomSample[
   IntegerDigits[
    If[100 < IntegerPart[nn*10^dig]/10^dig < 1000, 
     IntegerPart[nn*10^(dig - 3)], 
     If[10 < IntegerPart[nn*10^dig]/10^dig < 100, 
      IntegerPart[nn*10^(dig - 2)], 
      If[0.1 < IntegerPart[nn*10^dig]/10^dig < 1, 
       IntegerPart[nn*10^dig], 
       If[IntegerPart[nn*10^dig]/10^dig > 1, 
        IntegerPart[nn*10^(dig - 1)], 
        If[0.01 < IntegerPart[nn*10^dig]/10^dig < 0.1, 
         IntegerPart[nn*10^(dig + 1)], 
         IntegerPart[nn*10^(dig + 2)]]]]]]]]]; fg = 
 If[FromDigits[Take[ff, 1]] > 0.5, ff, 
  RandomSample[
   IntegerDigits[
    If[100 < IntegerPart[nn*10^dig]/10^dig < 1000, 
     IntegerPart[nn*10^(dig - 3)], 
     If[10 < IntegerPart[nn*10^dig]/10^dig < 100, 
      IntegerPart[nn*10^(dig - 2)], 
      If[0.1 < IntegerPart[nn*10^dig]/10^dig < 1, 
       IntegerPart[nn*10^dig], 
       If[IntegerPart[nn*10^dig]/10^dig > 1, 
        IntegerPart[nn*10^(dig - 1)], 
        If[0.01 < IntegerPart[nn*10^dig]/10^dig < 0.1, 
         IntegerPart[nn*10^(dig + 1)], 
         IntegerPart[nn*10^(dig + 2)]]]]]]]]]; fh = 
 If[FromDigits[Take[fg, 1]] > 0.5, fg, 
  RandomSample[
   IntegerDigits[
    If[100 < IntegerPart[nn*10^dig]/10^dig < 1000, 
     IntegerPart[nn*10^(dig - 3)], 
     If[10 < IntegerPart[nn*10^dig]/10^dig < 100, 
      IntegerPart[nn*10^(dig - 2)], 
      If[0.1 < IntegerPart[nn*10^dig]/10^dig < 1, 
       IntegerPart[nn*10^dig], 
       If[IntegerPart[nn*10^dig]/10^dig > 1, 
        IntegerPart[nn*10^(dig - 1)], 
        If[0.01 < IntegerPart[nn*10^dig]/10^dig < 0.1, 
         IntegerPart[nn*10^(dig + 1)], 
         IntegerPart[nn*10^(dig + 2)]]]]]]]]]; fi = 
 If[FromDigits[Take[fh, 1]] > 0.5, fh, 
  RandomSample[
   IntegerDigits[
    If[100 < IntegerPart[nn*10^dig]/10^dig < 1000, 
     IntegerPart[nn*10^(dig - 3)], 
     If[10 < IntegerPart[nn*10^dig]/10^dig < 100, 
      IntegerPart[nn*10^(dig - 2)], 
      If[0.1 < IntegerPart[nn*10^dig]/10^dig < 1, 
       IntegerPart[nn*10^dig], 
       If[IntegerPart[nn*10^dig]/10^dig > 1, 
        IntegerPart[nn*10^(dig - 1)], 
        If[0.01 < IntegerPart[nn*10^dig]/10^dig < 0.1, 
         IntegerPart[nn*10^(dig + 1)], 
         IntegerPart[nn*10^(dig + 2)]]]]]]]]];
m = FromDigits[RandomInteger[dig - ddd, 1]];
mm = FromDigits[RandomInteger[dig - ddd, 1]];
mmm = FromDigits[RandomInteger[dig - ddd, 1]];
mmmm = FromDigits[RandomInteger[dig - ddd, 1]];
mmmmm = FromDigits[RandomInteger[dig - ddd, 1]];
mmmmmm = FromDigits[RandomInteger[dig - ddd, 1]];
geni = Take[fi, {m, m + ddd - 1}];
fei = If[FromDigits[Take[geni, 1]] > 0.5, geni, 
   Take[fi, {mm, mm + ddd - 1}]];
ffi = If[FromDigits[Take[fei, 1]] > 0.5, fei, 
   Take[fi, {mmm, mmm + ddd - 1}]];
fgi = If[FromDigits[Take[ffi, 1]] > 0.5, ffi, 
   Take[fi, {mmmm, mmmm + ddd - 1}]];
fhi = If[FromDigits[Take[fgi, 1]] > 0.5, fgi, 
   Take[fi, {mmmmm, mmmmm + ddd - 1}]];
fii = If[FromDigits[Take[fhi, 1]] > 0.5, fhi, 
   Take[fi, {mmmmmm, mmmmmm + ddd - 1}]];
Text[Style[fii, Small, Purple]]
Text[Style[FromDigits[fii], Medium, Bold, Blue]]

Grid[{{"dig 1", "dig 2", "dig 3", "dig 4", "dig 5", "dig 6", "dig 7", 
   "dig 8", "dig 9", "dig 0"}, DigitCount[FromDigits[fii]]}, 
 Frame -> All, Background -> {None, {{LightRed, Green}}}]

ListPlot[fii, PlotRange -> {{0, ddd + 1}, {-1, 10}}, 
 PlotStyle -> PointSize[Medium], PlotTheme -> "Scientific", 
 Ticks -> Automatic]

div;
cc = ddd/%;
dd = FromDigits[Take[cc, {IntegerPart[Sum[1, {k, cc}]/2]}]];
Partition[fii, dd];
ArrayPlot[Partition[fii, dd], 
 ColorFunction -> ColorData["ThermometerColors"], Mesh -> All, 
 PixelConstrained -> True, MeshStyle -> Blue, PlotTheme -> "Detailed",
  PlotLegends -> Placed[{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, Below], 
 ImageSize -> 400]

PieChart[{DigitCount[FromDigits[fii]]}, 
 SectorOrigin -> {Automatic, 1}, 
 PlotTheme -> {"BoldScheme", "VibrantColor"}, 
 ChartElementFunction -> "NoiseSector", 
 ChartLabels -> {DigitCount[FromDigits[fii]]}, 
 ChartLegends -> {"1", "2", "3", "4", "5", "6", "7", "8", "9", "0"}]

The above example was used Pi and 1000-digit sampling was required, giving the following result (plus a thermal representation of the numbers, for extended visual representation with ArrayPlot, where the digit 0 is cold (blue) and the digit 9 it's hot (red)):

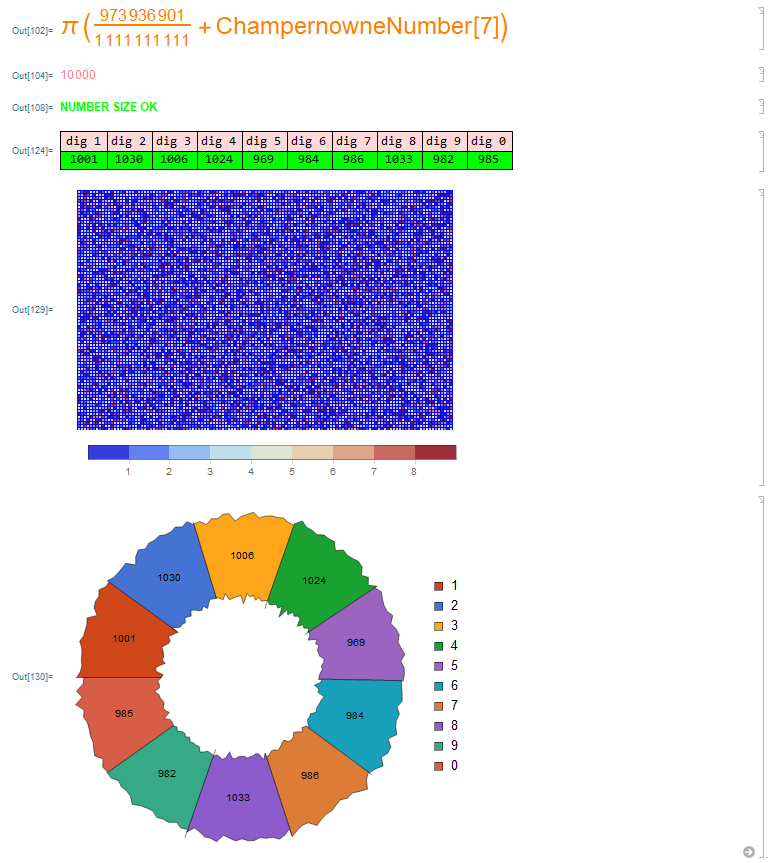
enter image description here

F) Use of large sampling through randomly efficient candidates

-For sample sizes of 5000+ digits.

-For use where it is desired to have high efficiency random sampling, without having to lock the digits unrealistically.

From a database of 534 numbers between Notable, Exotic and Synthetic Random Numbers, you can choose the 10 best in behavior: Deviation of the Arithmetical Mean (C), Deviation of the Count of digits of each type (S) and Deviation in Play of Coin (T) and make a ranking, which consequently generated the following table:

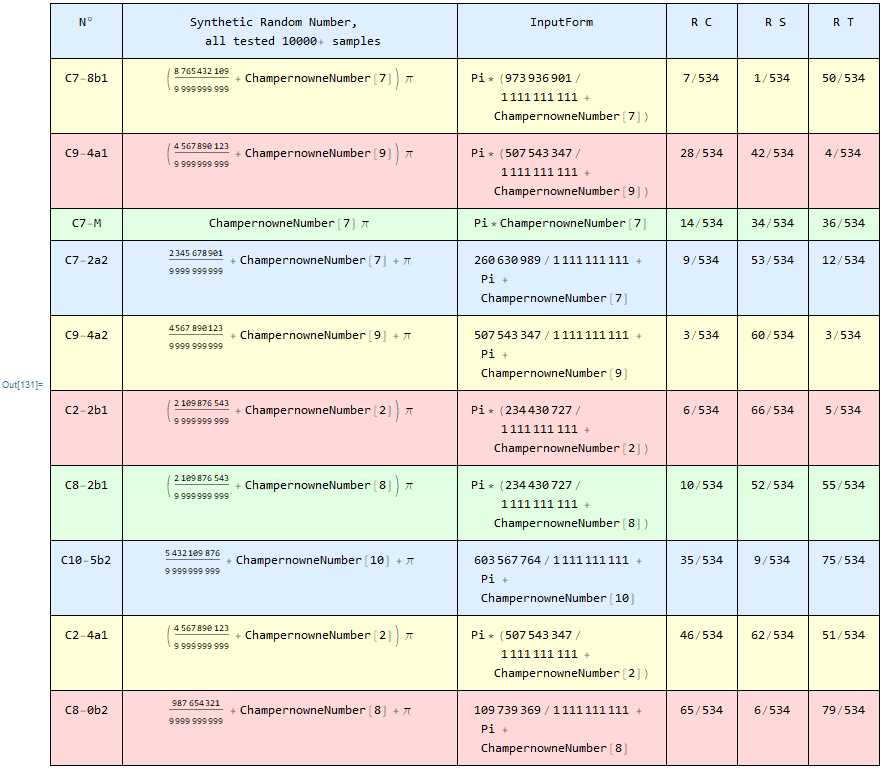
enter image description here

We can use any of these numbers to have good results in a solid way (especially in simulations that require low deviation values in means and vices).

The table above has the following code:

Grid[{{"N\[Degree]", 
   "Synthetic Random Number, all tested 10000+ samples ", "InputForm",
    "R C", " R S", 
   "R T"}, {"C7-8b1", ((8765432109/9999999999) + 
       ChampernowneNumber[7])*Pi // 
    HoldForm, ((8765432109/9999999999) + ChampernowneNumber[7])*Pi // 
    InputForm, "7/534", "1/534", 
   "50/534"}, {"C9-4a1", ((4567890123/9999999999) + 
       ChampernowneNumber[9])*Pi // 
    HoldForm, ((4567890123/9999999999) + ChampernowneNumber[9])*Pi // 
    InputForm, "28/534", "42/534", "4/534"}, {"C7-M", 
   ChampernowneNumber[7]*Pi // HoldForm, 
   ChampernowneNumber[7]*Pi // InputForm, "14/534", "34/534", 
   "36/534"}, {"C7-2a2", (2345678901/9999999999) + 
     ChampernowneNumber[7] + Pi // 
    HoldForm, (2345678901/9999999999) + ChampernowneNumber[7] + Pi // 
    InputForm, "9/534", "53/534", 
   "12/534"}, {"C9-4a2", (4567890123/9999999999) + 
     ChampernowneNumber[9] + Pi // 
    HoldForm, (4567890123/9999999999) + ChampernowneNumber[9] + Pi // 
    InputForm, "3/534", "60/534", 
   "3/534"}, {"C2-2b1", ((2109876543/9999999999) + 
       ChampernowneNumber[2])*Pi // 
    HoldForm, ((2109876543/9999999999) + ChampernowneNumber[2])*Pi // 
    InputForm, "6/534", "66/534", 
   "5/534"}, {"C8-2b1", ((2109876543/9999999999) + 
       ChampernowneNumber[8])*Pi // 
    HoldForm, ((2109876543/9999999999) + ChampernowneNumber[8])*Pi // 
    InputForm, "10/534", "52/534", 
   "55/534"}, {"C10-5b2", (5432109876/9999999999) + 
     ChampernowneNumber[10] + Pi // 
    HoldForm, (5432109876/9999999999) + ChampernowneNumber[10] + Pi //
     InputForm, "35/534", "9/534", 
   "75/534"}, {"C2-4a1", ((4567890123/9999999999) + 
       ChampernowneNumber[2])*Pi // 
    HoldForm, ((4567890123/9999999999) + ChampernowneNumber[2])*Pi // 
    InputForm, "46/534", "62/534", 
   "51/534"}, {"C8-0b2", (0987654321/9999999999) + 
     ChampernowneNumber[8] + Pi // 
    HoldForm, (0987654321/9999999999) + ChampernowneNumber[8] + Pi // 
    InputForm, "65/534", "6/534", "79/534"}}, Frame -> All, 
 Alignment -> Center, 
 Background -> {None, {{LightBlue, LightYellow, LightRed, 
     LightGreen}}}, Spacings -> {1.5, 1.5, 1.5}, 
 ItemSize -> {{4, 25, 15, 4, 4, 4}}]

Below is the sample result with a 10,000-digit sampling using a Synthetic Random Number candidate (one of the best random I got):

enter image description here
POSTED BY: Claudio Chaib
1 Reply
Sort By:

This version of the code below to generate random integers through real numbers, starting from a randomized part in the guide number, only makes the random shuffle after the number segment has been randomly selected (thus acquiring a behavior Even closer to the guide number:

num = Pi;
Text[Style[num, Large, Orange]]
ddd = 10;
Text[Style[ddd, Medium, Pink]]
dig = 100000;
nn = Abs[N[num, dig]];
div = Divisors[ddd];
hh = If[0.001 < nn < 1000, 
  Text[Style["NUMBER SIZE OK", Medium, Bold, Green]], 
  Text[Style["CHANGE NUMBER SIZE", Large, Bold, Red]]]
fi = IntegerDigits[
   If[100 < IntegerPart[nn*10^dig]/10^dig < 1000, 
    IntegerPart[nn*10^(dig - 3)], 
    If[10 < IntegerPart[nn*10^dig]/10^dig < 100, 
     IntegerPart[nn*10^(dig - 2)], 
     If[0.1 < IntegerPart[nn*10^dig]/10^dig < 1, 
      IntegerPart[nn*10^dig], 
      If[IntegerPart[nn*10^dig]/10^dig > 1, 
       IntegerPart[nn*10^(dig - 1)], 
       If[0.01 < IntegerPart[nn*10^dig]/10^dig < 0.1, 
        IntegerPart[nn*10^(dig + 1)], 
        IntegerPart[nn*10^(dig + 2)]]]]]]];
m = FromDigits[RandomInteger[dig - ddd, 1]];
mm = FromDigits[RandomInteger[dig - ddd, 1]];
mmm = FromDigits[RandomInteger[dig - ddd, 1]];
mmmm = FromDigits[RandomInteger[dig - ddd, 1]];
mmmmm = FromDigits[RandomInteger[dig - ddd, 1]];
mmmmmm = FromDigits[RandomInteger[dig - ddd, 1]];
geni = Take[fi, {m, m + ddd - 1}];
fei = If[FromDigits[Take[geni, 1]] > 0.5, geni, 
   Take[fi, {mm, mm + ddd - 1}]];
ffi = If[FromDigits[Take[fei, 1]] > 0.5, fei, 
   Take[fi, {mmm, mmm + ddd - 1}]];
fgi = If[FromDigits[Take[ffi, 1]] > 0.5, ffi, 
   Take[fi, {mmmm, mmmm + ddd - 1}]];
fhi = If[FromDigits[Take[fgi, 1]] > 0.5, fgi, 
   Take[fi, {mmmmm, mmmmm + ddd - 1}]];
fii = If[FromDigits[Take[fhi, 1]] > 0.5, fhi, 
   Take[fi, {mmmmmm, mmmmmm + ddd - 1}]];
cxc = RandomSample[fii];
fen = If[FromDigits[Take[cxc, 1]] > 0.5, cxc, RandomSample[fii]];
ffn = If[FromDigits[Take[fen, 1]] > 0.5, fen, RandomSample[fii]];
fgn = If[FromDigits[Take[ffn, 1]] > 0.5, ffn, RandomSample[fii]];
fhn = If[FromDigits[Take[fgn, 1]] > 0.5, fgn, RandomSample[fii]];
fin = If[FromDigits[Take[fhn, 1]] > 0.5, fhn, RandomSample[fii]];


Text[Style[fin, Small, Purple]]
Text[Style[FromDigits[fin], Medium, Bold, Blue]]

Grid[{{"dig 1", "dig 2", "dig 3", "dig 4", "dig 5", "dig 6", "dig 7", 
   "dig 8", "dig 9", "dig 0"}, DigitCount[FromDigits[fin]]}, 
 Frame -> All, Background -> {None, {{LightRed, Green}}}]

ListPlot[fin, PlotRange -> {{0, ddd + 1}, {-1, 10}}, 
 PlotStyle -> PointSize[Medium], PlotTheme -> "Scientific", 
 Ticks -> Automatic]

div;
cc = ddd/%;
dd = FromDigits[Take[cc, {IntegerPart[Sum[1, {k, cc}]/2]}]];
Partition[fin, dd];
ArrayPlot[Partition[fin, dd], 
 ColorFunction -> ColorData["ThermometerColors"], Mesh -> All, 
 PixelConstrained -> True, MeshStyle -> Blue, PlotTheme -> "Detailed",
  PlotLegends -> Placed[{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, Below], 
 ImageSize -> 400]

PieChart[{DigitCount[FromDigits[fin]]}, 
 SectorOrigin -> {Automatic, 1}, 
 PlotTheme -> {"BoldScheme", "VibrantColor"}, 
 ChartElementFunction -> "NoiseSector", 
 ChartLabels -> {DigitCount[FromDigits[fin]]}, 
 ChartLegends -> {"1", "2", "3", "4", "5", "6", "7", "8", "9", "0"}]
POSTED BY: Claudio Chaib
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract