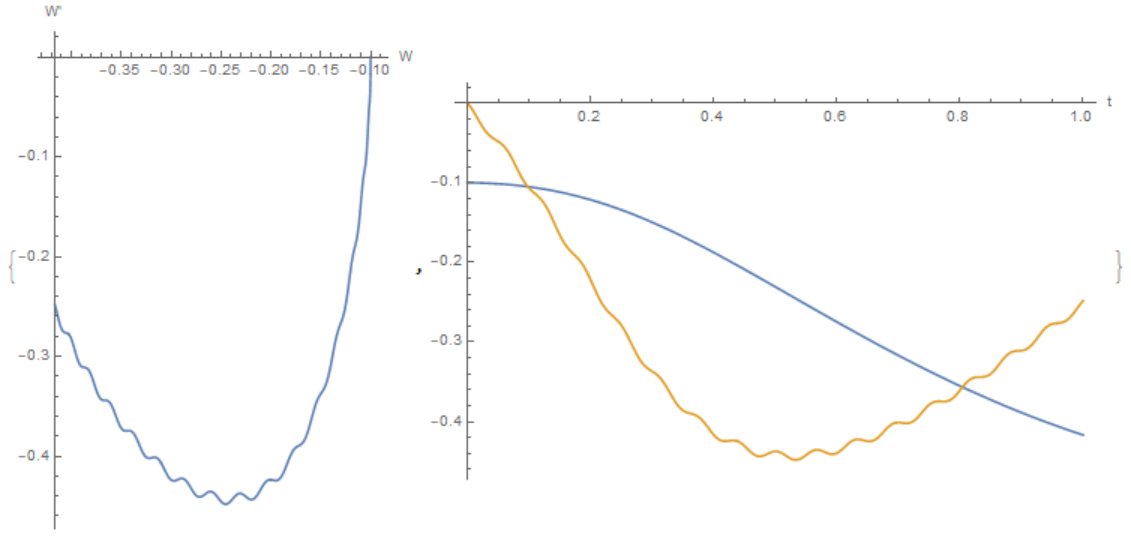
I will show a numerical solution
q = {U[t] + 3 U[t]^2 + 6 V[t] + 3 V[t]^2 + 5 W[t] + 2 W[t]^2 +
4 U[t]*V[t] == 2 U'[t],
6 U[t] + 3 U[t]^2 + 3 V[t] + 4 V[t]^2 + 8 W[t] + 4 W[t]^2 +
3 U[t]*V[t] == V'[t],
5 U[t] + 3 U[t]^2 + 5 V[t] + 3 V[t]^2 + 8 W[t] + 4 W[t]^2 +
8 U[t] V[t] + Q*Sin[100*t] == W'[t] + 2 W''[t]};
ic = {U[0] == a, V[0] == a, W[0] == a, W'[0] == 10^-4};
Q = -1; a = -1/10; tm = 1;
p = NDSolveValue[{eq, ic}, {W[t], W'[t]}, {t, 0, tm}];
{ParametricPlot[p, {t, 0, tm}, PlotRange -> All,
AxesLabel -> {"W", "W'"}],
Plot[p, {t, 0, tm}, PlotRange -> All, AxesLabel -> {"t", ""}]}