Mariusz did a great job !

But his explanation is somewhat short. Unfortunately I can't access your data, but I would proceed as follows.

Looking at your data-points there seems to be something like a straight line at the right and left end. Get some of the first and some of the last data and do a linear fit, then you will get a first approximation of a linear function to be used as "baseline". Then extract the data in the middle. These could be a Gaussian like

a + b Exp[ w ( x - x0 )^2 ]

a is something around 100, b as well and w has something to do with the half-width, which can be estimated as about 0.02. So find a value for w. Fit it to the extracted data, and you will get starting parameters for the overall fit of all your data to

a + b Exp[ w ( x - x0 )^2 ]  + c x 

I'm use Trial and Error,and knowledge of function properties (like Gaussian,and line),and that's all.

Regards Mariusz.

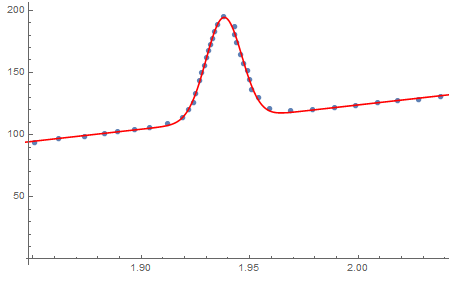
Adjustment:

 data = Import["a.csv", "table", FieldSeparators -> " "];
 nlm = NonlinearModelFit[data, 
    d + a*Exp[-(x - b)^2/2 c^2], {{a, 100}, {b, 1.94}, {c, 90}, {d, 
      95}}, x];
 nlm["AdjustedRSquared"];
 nlm[x];
 nlm["ParameterTable"];
 dataplot = ListPlot[data];
 fitplot = 
   Plot[nlm[x], {x, 1.8, 2.10}, PlotStyle -> Red, PlotRange -> All];
 Show[dataplot, fitplot]

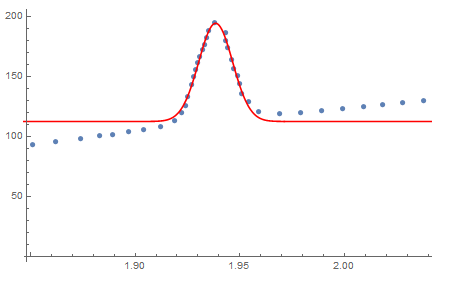
A better model:

 data = Import["a.csv", "table", FieldSeparators -> " "];
 nlm = NonlinearModelFit[data, 
    d + a*Exp[-(x - b)^2/2 c^2] + 
     e*x, {{a, 100}, {b, 1.94}, {c, 90}, {d, 95}, {e, 200}}, x];
 nlm["AdjustedRSquared"];
 nlm[x];
 nlm["ParameterTable"];
 dataplot = ListPlot[data];
 fitplot = 
   Plot[nlm[x], {x, 1.8, 2.10}, PlotStyle -> Red, PlotRange -> All];
 Show[dataplot, fitplot]