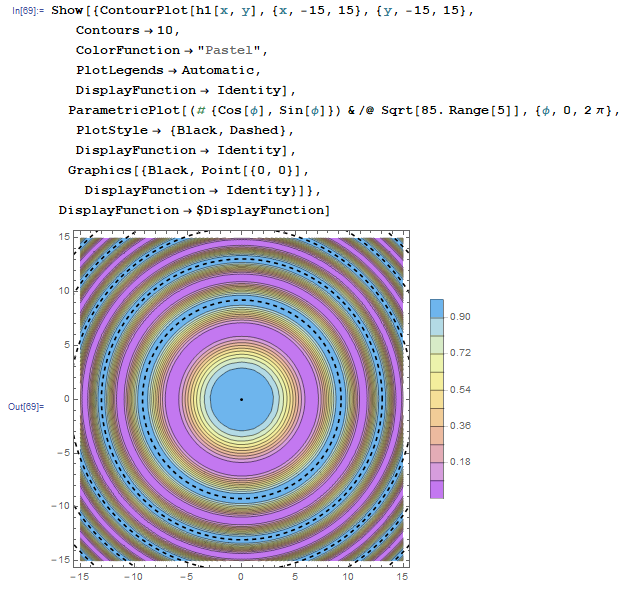
It looks very cool.

Sure. Just for the logs, ContourPlot[] must not be used where it does not fit

Clear[h, h1, h1r]
h[x_, y_, w_] := Cos[2 \[Pi] (x^2 + y^2)/(2 5 w)]^2
h1[x_, y_] := h[x, y, 17.]
h1r[r_] := Cos[2 \[Pi] r^2/170.]^2

combine three different 2D graphics into one plot

Show[{ContourPlot[h1[x, y], {x, -15, 15}, {y, -15, 15},
   Contours -> 10, 
   ColorFunction -> "Pastel",
   PlotLegends -> Automatic,
   DisplayFunction -> Identity],
  ParametricPlot[(# {Cos[\[Phi]], Sin[\[Phi]]}) & /@ 
    Sqrt[85. Range[5]], {\[Phi], 0, 2 \[Pi]},
   PlotStyle -> {Black, Dashed},
   DisplayFunction -> Identity], 
  Graphics[{Black, Point[{0, 0}],
    DisplayFunction -> Identity}]},
 DisplayFunction -> $DisplayFunction]

as

Your commands above do not seem to hang together as a complete set. You define h, which is not then used (did you mean h1?).

In the next line, you have h1 u1 = ...

Are h1 and u1 supposed to be multiplied together? If so, why are you then assigning to them (with a single = sign) as though they were a variable? What does this mean?

You seem to be using h1 as a function, taking parameters x and y. But in that case, should you not define it by, say

h1[x_, y_] := Cos[(2[Pi] ((x)^2 + (y)^2)/(25 w))]^2

From what I can tell, you seem to have a number of confusions. I suggest you look at some examples of ContourPlot and gradually adapt them towards what you want.