Open in Cloud | Download to Desktop via Attachments Below
For ? Day. 2015, Wolfram Research stirred up publicity with the blog "Pi or Pie?! Celebrating Pi Day of the Century (And How to Get Your Very Own Piece of Pi)":
https://blog.stephenwolfram.com/2015/03/pi-or-pie-celebrating-pi-day-of-the-centuryand-how-to-get-your-very-own-piece-of-pi
I grumbled that no self-respecting Deity would bother sending clues to worshipers dumb enough to use decimal instead of continued fractions (CF). However, in 2019 we're barely able to afford a full CF version of Wolfram's birthday games. Assuming GaussKuzmin distribution, define

Then

I.e, 41.5% of terms should be 1, 17% should be 2, etc. But cfprob also gives us the probabilities of term sequences:

(Invariant under reversal but not shuffling.)
This says to expect about six 1,2,3's in every burst of 1000 terms:

Try a million :
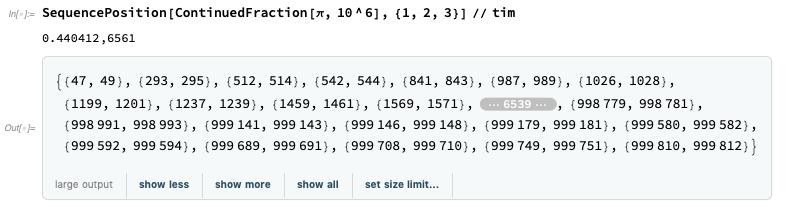
(0.5 seconds for a million terms. Have I actually lived to see this?)

Continued fractions accommodate fancier date formats:

Sure enough, there were two of them.
But for really fancy dates,

we'll need Eric Weisstein's record ? CF calculation.
Utility functions
These are the definitions of the utility function tim you will need for the above evaluations:

 Attachments:
Attachments: