Recently, I was asked to assist somebody with graphing the Fourier transform of an image. The resulting images were neat, and the work reminded me of a really fun application of Fourier transforms: Hybrid Images
By taking the Fourier transforms of two images, and combining the high-frequency parts of one with the low-frequency parts of the other, you get an image that looks like one thing when your eyes are focused, and another thing when they are unfocused. The classic example is the Einstein Marilyn Monroe image.

Of course, the above example is in black and white, so a natural extension would be to include color. Also, I would like to explore how the image changes as I vary how much of each image is included.
Thankfully, both of these things are easy to do in the Wolfram Language.
As a warmup, lets simply visualize the Fourier transform of an image by itself. I use one of the test images provided in ExampleData[].
mandrill=ExampleData[{"TestImage","Mandrill"}]

mandrill2 = ColorSeparate[mandrill]

With the ColorSeparate function, I split the image into its RGB channels. I will be taking the Fourier transform of each of these.
shift := Table[(-1)^(i + j) #[[i]][[j]], {i, 1, Length[#]}, {j, 1, Length[#[[1]]]}] &
mandrill3 = Fourier[shift@ImageData@#] & /@ mandrill2;
Before taking the transform, I apply a function shift to the image, so that the low frequencies of the image will appear at the center of the Fourier transformed image, rather than at the edges.
ColorCombine[Image /@ Abs[mandrill3]]

And there we have the Fourier transform of our mandrill.
To put it all together, we could write this as
ColorCombine[
Image /@ Abs /@
Fourier /@ shift /@ ImageData /@ ColorSeparate[mandrill]]
Now that weve got the warm-up out of the way, we want to take two different images, and mix them together. Well need two images that are the same size, so Ill set it to manually resize the images to 512*512. All the example images are that size already, but you may need to resize if you want to use something else.
size = 512;
test1 = ImageResize[ExampleData[{"TestImage", "Mandrill"}], size];
test2 = ImageResize[ExampleData[{"TestImage", "Peppers"}], size];
ft1 = Fourier /@ shift /@ ImageData /@ ColorSeparate[test1];
ft2 = Fourier /@ shift /@ ImageData /@ ColorSeparate[test2];
Now we can make a temporary variable based on one image, and replace a square of size 2x in the center of the Fourier-transformed image with the corresponding elements of the other image.
Manipulate[
Module[{temp = ft1},
temp[[1;;3,size/2-x;;size/2+x,size/2-x;;size/2+x]]=ft2[[1;;3,size/2-x;;size/2+x,size/2-x;;size/2+x]];
ColorCombine[Image/@Abs/@InverseFourier/@temp]],
{x,1,size/2-1,1}]
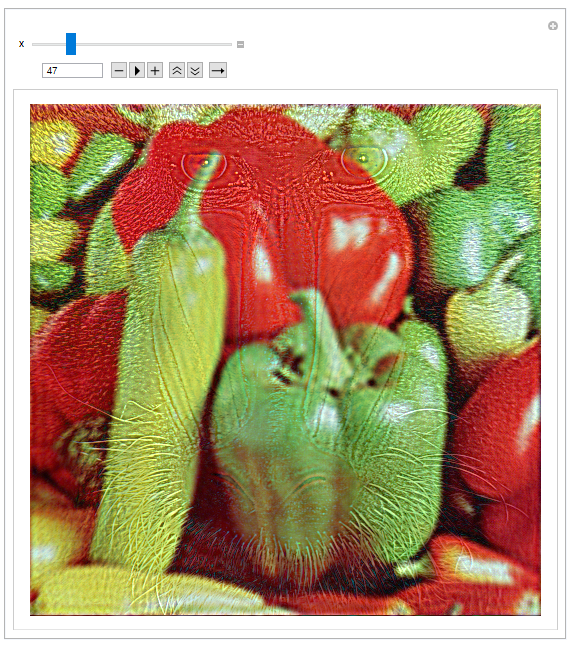
This generates a manipulate box where you can control how much of each image is included. For this example I find that x=45 or so is the sweet spot for making the Mandrill 'hidden' when seen from afar, as included at the top of the post. We can also swap the two images, and have some hidden peppers in a picture of a Mandrill.
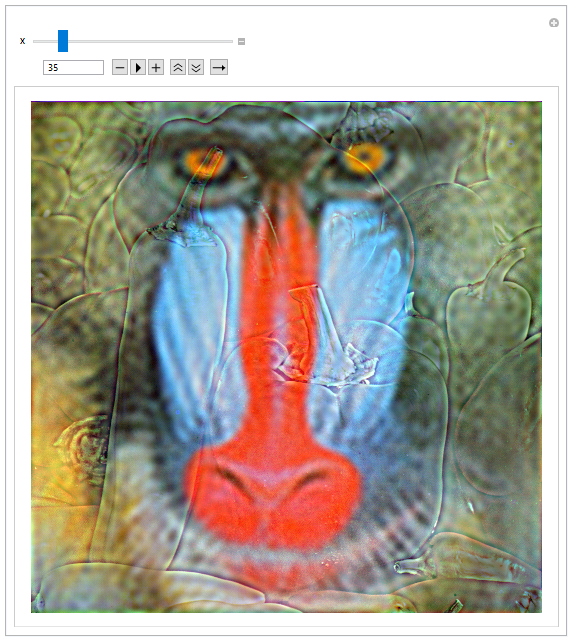
Hopefully, some of you find this as fun as I do. I attach the notebook I used to generate these hybrid images.
 Attachments:
Attachments: