Message Boards Message Boards

Simulating Finite Automata (and making it look nice)

The simulation in action

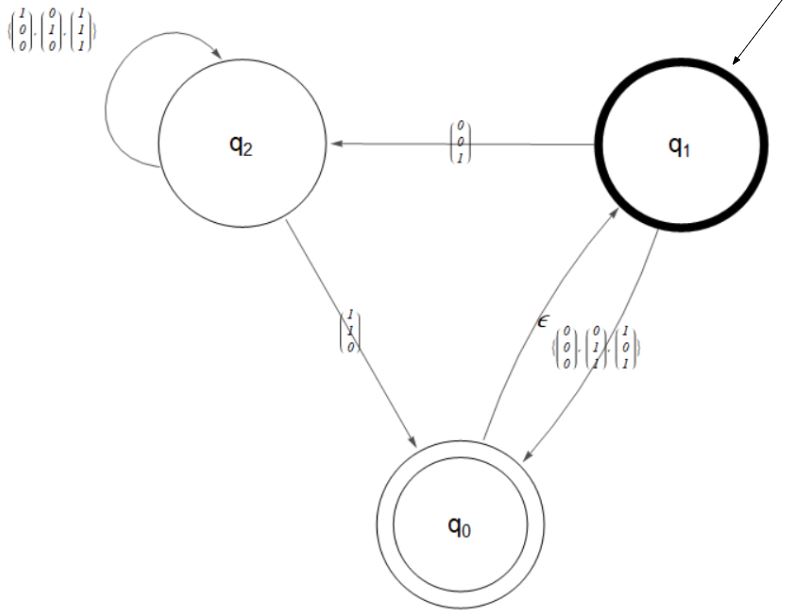
a plot of a nondeterministic finite automaton, AddBin3 that recognizes a set of 3-digit binary numbers whos first two columns add up to its' third colum The above nondeterministic finite automaton recognizes a language I will call AddBin3. The alphabet for this NFA is the set of 3-digit binary numbers ({0,0,0},{0,0,1},...{1,1,1}}. The language includes all strings whose first 2 rows add up to the third row. So {1,0,1} (1+0=1} would be part of the language and {0,0,1},{1,1,0} (01+01=10), but not {1,1,1}.
To simulate the states the automaton passes given a certain input string is fairly simple using FoldList. We simply pass it the initial state, a set of rules and the input, then apply the rules repeatedly to the set of states. 

rule = <|{1, {0, 0, 0}} -> {0, 
     1}, {1, {0, 0, 1}} -> {2}, {1, {0, 1, 0}} -> {}, {1, {0, 1, 
      1}} -> {0, 1},
   {1, {1, 0, 0}} -> {}, {1, {1, 0, 1}} -> {0, 
     1}, {1, {1, 1, 0}} -> {}, {1, {1, 1, 1}} -> {},
   {2, {0, 0, 0}} -> {}, {2, {0, 0, 1}} -> {}, {2, {0, 1, 
      0}} -> {2}, {2, {0, 1, 1}} -> {},
   {2, {1, 0, 0}} -> {2}, {2, {1, 0, 1}} -> {}, {2, {1, 1, 0}} -> {0, 
     1}, {2, {1, 1, 1}} -> {2},
   {0, {0, 0, 0}} -> {}, {0, {0, 0, 1}} -> {}, {0, {0, 1, 
      0}} -> {}, {0, {0, 1, 1}} -> {},
   {0, {1, 0, 0}} -> {}, {0, {1, 0, 1}} -> {}, {0, {1, 1, 
      0}} -> {}, {0, {1, 1, 1}} -> {}
   |>;
FoldList[Union @@ (Function[s, rule[{s, #2}]] /@ #1) &, {1}, {{0, 0, 
   1}, {1, 1, 0}, {1, 0, 1}}]

Output: {{1}, {2}, {0, 1}, {0, 1}} As we see, the automaton starts in state 1, moves to state 2, then moves on to states 0 and 1.
To make this nicer to read, I made a more elaborate version, which has more information (the initial state, the accept state(s), the rule, etc. It outputs a quite elaborate StringTemplate that I thought was worth sharing.

addBin3Simulation[input_List]:=
((*set the initial state, accept state(s), alphabet, and rules*)
initialstate={1};
acceptstates= {0};
alphabet={{0,0,0},{0,0,1},{0,1,0},{0,1,1},{1,0,0},{1,0,1},{1,1,0},{1,1,1}};
rule=<|{1,{0,0,0}}->{0,1},{1,{0,0,1}}->{2},{1,{0,1,0}}->{},{1,{0,1,1}}->{0,1},
{1,{1,0,0}}->{},{1,{1,0,1}}->{0,1},{1,{1,1,0}}->{},{1,{1,1,1}}->{},
{2,{0,0,0}}->{},{2,{0,0,1}}->{},{2,{0,1,0}}->{2},{2,{0,1,1}}->{},
{2,{1,0,0}}->{2},{2,{1,0,1}}->{},{2,{1,1,0}}->{0,1},{2,{1,1,1}}->{2},
{0,{0,0,0}}->{},{0,{0,0,1}}->{},{0,{0,1,0}}->{},{0,{0,1,1}}->{},
{0,{1,0,0}}->{},{0,{1,0,1}}->{},{0,{1,1,0}}->{},{0,{1,1,1}}->{}
|>;
(*Fold the rule over and over on the states to get a list of the sequence of states*)
states=FoldList[Union@@(Function[s,rule[{s,#2}]]/@#1)&,initialstate,input];
(*check that all the characters in the input string are part of the alphabet*)
If[ContainsOnly[input,alphabet],
    (*if they are, output the result of the simulation*)
    StringRiffle[
       Join[
         (*First, output the initial state*)
         {StringTemplate["The intial state of the NFA is \!\(\*SubscriptBox[\(q\), \(``\)]\)`"][initialstate]},
         (*Then, show the sequence of states reached through the input*)
         (*adjust the output depending on the number of states for correct grammar*)
         (*have a special output for an empty list*)
MapThread[StringTemplate["After the next input `1`, the new state <*
                 If[Length[#2]==1, 
                 \" is \"<>#2[[1]], 
                 \"s are\" <>
                   If[Length[#2]==0, 
                    \" none. The NFA terminates here.\", 
                    StringRiffle[Most[#2],{\" \", \",\", \" and \"}]
                        <>Last[#2]]]*>"],
          {input,Map[StringTemplate["\!\(\*SubscriptBox[\(q\), \(`1`\)]\)"],Rest[states],{2}]}
                 (*terminate the MapThread loop after the first empty list*)
                 [[All,;;FirstPosition[Rest[states],{},{-1}][[1]]]]],
         (*attach a statement weather the string was accepted or not*)
         {If[Last[states]!= {},
          "This is the last state and "<>If[ContainsAny[Last[states],acceptstates],
                              "the string is accepted.", 
                              "the string is not accepted."],
          "The string is not accepted."]}],
       "\n"],
    (*if the input characters are not all in the alphabet, output an error message*)
    "Error: One or more of the input characters are not in the alphabet"])

When we give this function an input string, it will give us information in an easily digestible format.
Some examples: enter image description here The function will also give an Error when the string has characters that are not in the language.
Of course, this function can be generalized for other NFAs:

(*generalied NFA simulation*)
nfaSimulation[alphabet_List, initialstate_List, rule_Association, 
  acceptstates_List, input_List] :=
 ((*Fold the rule over and over on the states to get a list of the \
sequence of states*)
  states = 
   FoldList[Union @@ (Function[s, rule[{s, #2}]] /@ #1) &, 
    initialstate, input];
  (*check that all the characters in the input string are part of the \
alphabet*)
  If[ContainsOnly[input, alphabet],
    (*if they are, output the result of the simulation*)
    StringRiffle[
           Join[
           (*First, output the initial state*)
           {StringTemplate[
        "The intial state of the NFA is \!\(\*SubscriptBox[\(q\), \
\(``\)]\)`"][initialstate]},
           (*Then, 
     show the sequence of states reached through the input*)
           (* 
     adjust the output depending on the length of the list of states \
to have correct grammar*)
           (*have a special output for an empty list*)     
     MapThread[
      StringTemplate[
       "After the next input `1`, the new state <*If[Length[#2]==1, \
\" is \"<>#2[[1]], \"s are\" <>If[Length[#2]==0, \" none. The NFA \
terminates here.\", StringRiffle[Most[#2],{\" \", \",\", \" and \
\"}]<>Last[#2]]]*>"],
                {input, 
        Map[StringTemplate["\!\(\*SubscriptBox[\(q\), \(`1`\)]\)"], 
         Rest[states], {2}]}
                      (*terminate the MapThread loop after the first instance \
of an empty list*)
                      [[All, ;; FirstPosition[Rest[states], {}, {-1}][[1]]]]],
           (*attach a statement weather the string was accepted or not*)
\

           {If[Last[states] != {},

       "This is the last state and " <> 
        If[ContainsAny[Last[states], acceptstates],
                                       "the string is accepted.", 
                                       "the string is not accepted."],
                 "The string is not accepted."]}],
           "\n"],
    (*if the input characters are not all in the alphabet, 
   output an error message*)
    "Error: One or more of the input characters are not in the \
alphabet"])

We just need to give this function the alphabet, initial state, rule, acceptstates and an input and it will generate a narrative about the computation of the NFA. a generalized version of the simulator in action

Bonus: here is how I draw NFAs with the WL.

nfaPlot[q_, q0_, transitions_, f_, 
  opts___] := (g \[Function] 
    Graph[g, 
     VertexShape -> 
      Join[Thread[
        Complement[VertexList[g], f, {q0}] -> Graphics[Circle[]]], 
       Thread[DeleteCases[f, q0] -> 
         Graphics[{Circle[], Circle[{0, 0}, 0.8]}]], {q0 -> 
         Graphics[{If[MemberQ[f, q0], Circle[{0, 0}, 0.8], Nothing], 
           Thickness[0.05], Circle[]}]}], VertexSize -> Large, 
     EdgeStyle -> Black, opts])@
  Graph[q, Labeled[#1 \[DirectedEdge] #2, 
      If[Length[#3] === 1, #3[[1]], #3]] & @@@ 
    KeyValueMap[Append, 
     GroupBy[transitions, (#[[;; 2]] &) -> (#[[3]] &)]]]
nfaPlot[Labeled[#, Style[Subscript["q", #], Large], Center] & /@ {0, 
   1, 2}, 0, 
 MapAt[Style[#, Large, Italic, 
    FontFamily -> "Times New Roman"] &, {{0, 1, 1}, {1, 2, 1}, {2, 0, 
    1}, {1, 0, 0}, {2, 1, 0}, {0, 2, 0}}, {All, 3}], {2}]

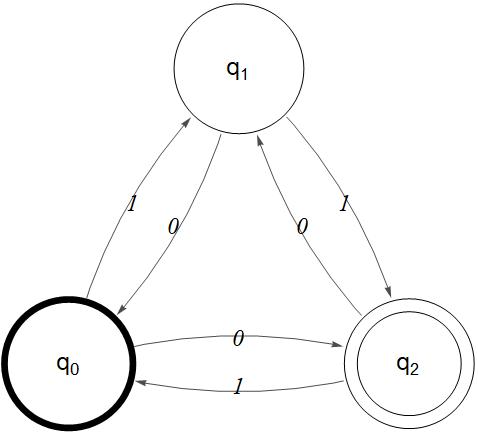
The output looks like the image below. The initial state is marked by a bold circle, but feel free to manually draw an arrow leading into the diagram like I did above:
an example DFA
POSTED BY: Katja Della Libera
1 Reply
Sort By:

enter image description here - Congratulations! This post is now a Staff Pick as distinguished by a badge on your profile! Thank you, keep it coming, we are looking forward to more of your posts!

POSTED BY: Moderation Team
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract