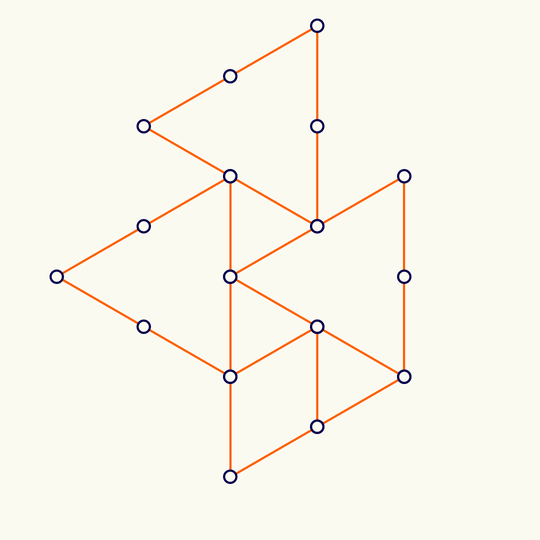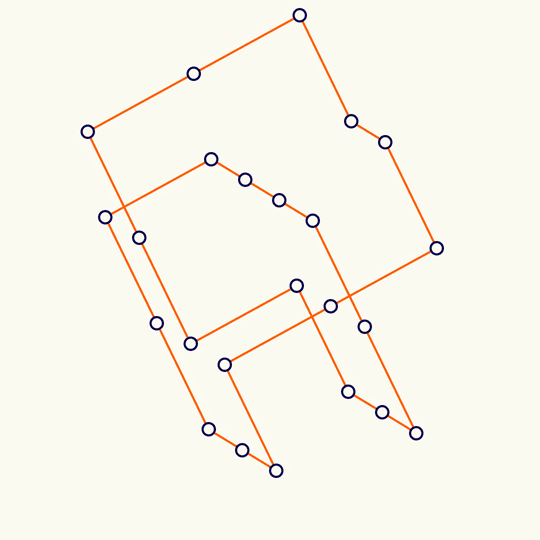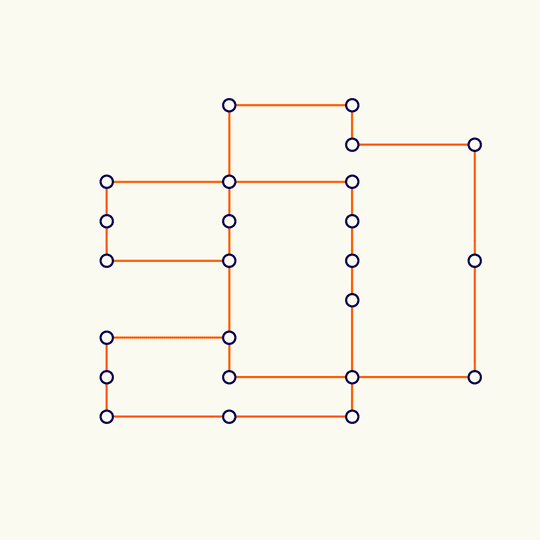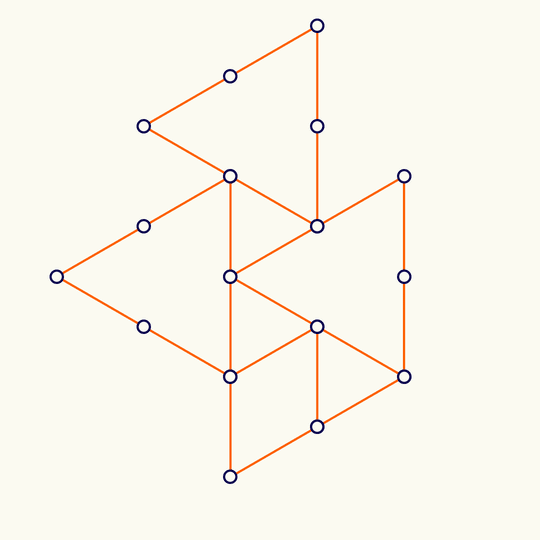
Minimal
This shows the trefoil knot lying on the simple cubic lattice with the fewest possible number of edges (it's a theorem of Yuanan Diao that the lattice stick number of the trefoil is 24), rotated, and projected to the plane.
The 3D vertex locations are in KnotPlot. At least in the MacOS version of KnotPlot, the data is contained in the app bundle at /Applications/KnotPlot/KnotPlot.app/Contents/Resources/special/mscl/3.1; if you don't have KnotPlot installed, you can download the data by going to https://knotplot.com/download/ and clicking the link to download kpdist.tar.gz. If you do that and then unzip to get a directory called kpsdist, the following commands will import the vertices and mean center:
lattice31 = Import["kpdist/special/mscl/3.1", "Table"];
lattice31 = lattice31 - Table[Mean[lattice31], {Length[lattice31]}];
As usual for animations where I want to smoothly stop and start a motion, I'm going to use the smootheststep function:
smootheststep[t_] := -20 t^7 + 70 t^6 - 84 t^5 + 35 t^4;
Here, then, is the Manipulate for the above animation (the giant obnoxious Which is to switch between different axis rotations, which I obviously could have made a little cleaner with some extra work):
DynamicModule[{p, q, a, b, n, M, θ, pl,
cols = RGBColor /@ {"#fd5f00", "#05004e", "#fbfaf1"}},
Manipulate[
Which[t < 1 || t == 4,
{p, q} = RotationMatrix[ArcTan[1/Sqrt[2]]].{Normalize[{1, 1, 0}], {0, 0, 1}};
θ = -(ArcTan[1/Sqrt[2]] + Pi/2) smootheststep[Mod[t, 1]];
{n, b} = RotationMatrix[θ].{p, q};,
1 <= t < 2,
{p, q} = {{0, 0, 1}, {-(1/Sqrt[2]), -(1/Sqrt[2]), 0}};
θ = (Pi - ArcTan[Sqrt[23 - 16 Sqrt[2]]]) smootheststep[Mod[t, 1]];
{n, b} = RotationMatrix[-θ,
N@{Sqrt[1/17 (5 + 2 Sqrt[2])], Sqrt[1/17 (7 - 4 Sqrt[2])],
Root[1 - 10 #1^2 + 17 #1^4 &, 1]}].# & /@ {p, q};,
2 <= t < 3,
{p, q} = {{-1, 0, 0}, {0, 0, 1}};
θ = 3 Pi/4 smootheststep[Mod[t, 1]];
{n, b} = RotationMatrix[θ].{p, q},
3 <= t,
{p, q} = {{1/Sqrt[2], 0, -(1/Sqrt[2])}, {-(1/Sqrt[2]), 0, -(1/Sqrt[2])}};
θ = (Pi - ArcCot[(3 - 2 Sqrt[2] + 2 Sqrt[3] + Sqrt[6])/Sqrt[
13 - 4 Sqrt[3] + 2 Sqrt[6]]]) smootheststep[Mod[t, 1]];
{n, b} = RotationMatrix[-θ,
N@{Root[1 - 156 #1^2 + 1670 #1^4 - 5148 #1^6 + 4801 #1^8 &,
1], Root[1 - 52 #1^2 + 870 #1^4 - 5044 #1^6 + 4801 #1^8 &,
2], (2 + Sqrt[2])/Sqrt[
94 - 48 Sqrt[2] + 48 Sqrt[3] - 32 Sqrt[6]]}].# & /@ {p, q};
];
a = Cross[b, n];
M = {a, b};
pl = M.# & /@ lattice31;
Graphics[
{Thickness[.004], cols[[1]], Line[Append[#, First[#]] &[pl]],
FaceForm[cols[[-1]]],
EdgeForm[Directive[Thickness[.004], cols[[2]]]],
Disk[M.#, .05] & /@ Sort[lattice31, n.#1 > n.#2 &]},
ImageSize -> 540, PlotRange -> 2.2, Background -> cols[[-1]]],
{t, 0, 4}]
]