Let me give you a little background first.
The formula I'm trying to calculate is below:
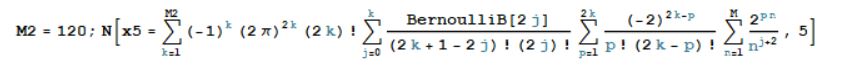
Note it converges if M is finite, but not infinite. But then, below I have a formula which gives an analytic continuation for the infinite sum over
$n$ which converges even if
$m>0$ (if
$m<0$ both the left and the right-hand sides converge and they match, if
$m>0$ only the right-hand side converges -- note that below
$M=\infty$):

Now, to make things simpler, let's try to sum up everything together for a large M2. Let's ignore the complex part, because for positive
$m$ only the last term is complex. I could've used better variable names, but darn Mathematica made N a reserved keyword.
Hence altogether the sum I need to calculate is this little monster: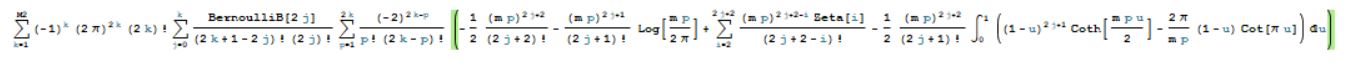
And the input formula is:
M2 = 100; m = Log[2];
N[Sum[(-1)^k*(2*Pi)^(2*k)*(2*k)!*
Sum[(BernoulliB[2*j]/((2*k + 1 - 2*j)!*(2*j)!))*
Sum[((-2)^(2*k -
p)/(p!*(2*k - p)!))*((-(1/
2))*((m*p)^(2*j + 2)/(2*j + 2)!) - ((m*p)^(2*j +
1)/(2*j + 1)!)*Log[(m*p)/(2*Pi)] +
Sum[((m*p)^(2*j + 2 - i)*Zeta[i])/(2*j + 2 - i)!, {i, 2,
2*j + 2}] - (1/2)*((m*p)^(2*j + 2)/(2*j + 1)!)*
Integrate[(1 - u)^(2*j + 1)*
Coth[(m*p*u)/2] - ((2*Pi)/(m*p))*(1 - u)*Cot[Pi*u], {u,
0, 1}]), {p, 1, 2*k}], {j, 0, k}], {k, 1, M2}], 10]