Hi there, I've been working on a little project, an inverted pendulum with reaction wheel for a while now. I've managed to get it working a bit, as seen in this following animation and code:

verifiedp = {mb -> 0.088`, mw -> 0.12931`, x -> 0.060519`, 
   y -> 0.061816`, l -> 0.08650876959592016`, k -> 0.09`, 
   rw -> 0.000039255383907286545`, 
   jw -> 0.0004032497194086029` (*jw \[Rule] 
   3.74703\[Times]10^-4*), \[Tau] -> 0.0335`, g -> 9.81`, 
   rb -> 0.00016799999999999996`, 
   jb -> 0.001412, \[Mu] -> 0.000795, \[Iota] -> 0.1}

displacement = 5 \[Pi]/180;
bump[t_] := 
 0.5 E^(-10 (t - 3)^2) - 0.8 E^(-10 (t - 7.5)^2) - 
  1/2 E^(-10 (t - 13)^2)

deqns = {g (l mb + k mw) Sin[\[Theta][t]] + 
   jb (\[Theta]^\[Prime]\[Prime])[t] == -\[Mu] ArcTan[
     Derivative[1][\[Theta]][t]/\[Iota]] + 
   1/2 x Cos[\[Theta][t]] f[t] + y Cos[\[Theta][t]] f[t] - 
   rb Derivative[1][\[Theta]][t] + jw (\[Phi]^\[Prime]\[Prime])[t], 
 jw (\[Phi]^\[Prime]\[Prime])[t] == \[Tau] u[t] - 
   rw Derivative[1][\[Phi]][t] - jw (\[Theta]^\[Prime]\[Prime])[t]}

nlmodel = 
  NonlinearStateSpaceModel[
    deqns, {{\[Theta][t], 0}, {\[Theta]'[t], 0}, {\[Phi]'[t], 0}}, {u[
      t], f[t]}, {\[Theta][t]}, t] /. verifiedp;

nq = DiagonalMatrix[{3000, 0.1, 0.5}];
nr = 20 {{1}}; nonlineargains = 
 Join[Last@
    CoefficientArrays[LQRegulatorGains[{nlmodel, 1}, {nq, nr}]] // 
   Normal, {ConstantArray[0, 3]}];
controlmodelnl = 
  SystemsModelStateFeedbackConnect[nlmodel, nonlineargains];
{thetanl, thetadotnl, phidotnl} = 
  StateResponse[{controlmodelnl, {displacement, 0, 0}}, {0, 
    bump[t]}, {t, 15}];
outputnl = 
  OutputResponse[{controlmodelnl, {displacement, 0, 0}}, {0}, {t, 15}];
nonlineargains[[1]] // MatrixForm
controlforcenl = -nonlineargains[[
     1]].{\[Theta][t], \[Theta]'[t], \[Phi]'[t]};

Orange is the body angle, multiplied by 30 (just so I can see it on the plot compared to phi'[t] Blue is the angular velocity of the motor.

As one can see, a nice smooth OutPut[] and StateResponse[] of a pretty quick to stabilize system.

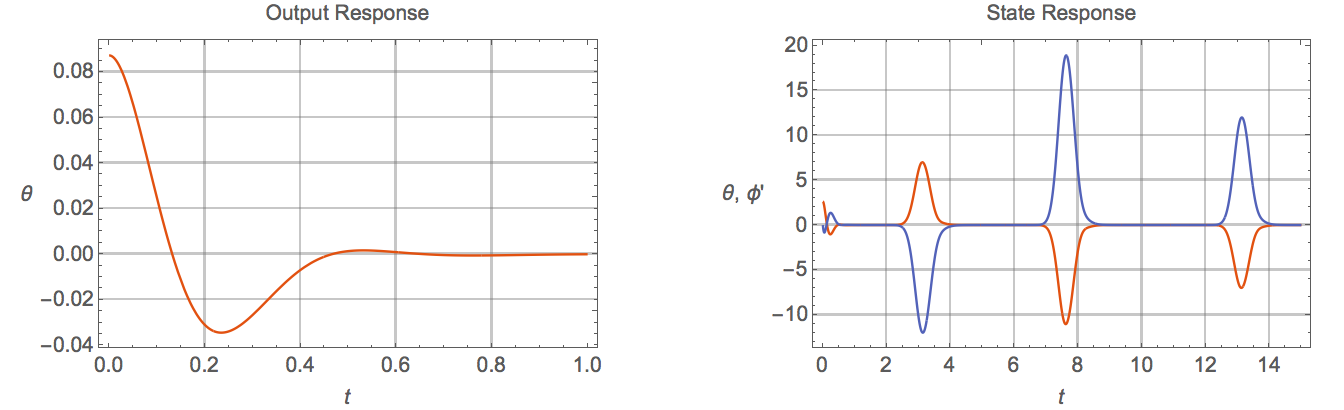
To explain the code a bit:

• Theta[t] is the pendulums measured angle
• Phi'[t] is the angular velocity of the motor
• u[t] is the control signal
• f[t] is an external force
• bump[t] said external force

Anyways, This is all fine, however the Sensors of my IMU are pretty noisy, and need to be filtered, in the beginning I used a madgwick filter, however the phase displacement was huge and my system could never become stable, afterwards I tried to use a complimentry filter, and a kalman. all of these successfully filtered my sensor readings but always added a phase displacement to my resulting measured body angle causing chaos.

I realized (after too much time) that my controlling model in mathematica doesn't have the filtered IMU data that my programmed MCU has and this needs to be included in my controlling scheme/loop in order to get myself proper gains.

So my question is, How can I simulate/add noise to the output/feedback of my NonLinearSystemModel, so I can add an observer and/or filter to my loop to calculate proper gains? I have looked at LQRegulator[], however I just don't get the syntax of the function, or really know if that is actually a proper example.

Thank you for the help. I'll gladly give more data/code/infos if requested.