This post is a summary of a problem identified in a longer post on Mathematica StackExchange which can be found here.
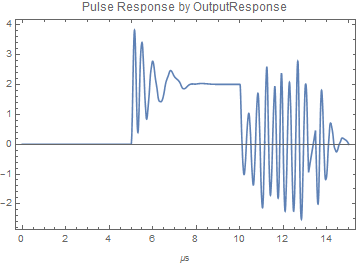
The issue identified is inaccurate numerical simulation provided by the function OutputResponse applied to a TransferFunctionModel. A two-pole model for a feedback amplifier is developed as a transfer function in the s-domain, and then as a TransferFunctionModel. The transfer function has 2 complex conjugate poles in the left half plane but close to the imaginary axis. The expected response to a pulse is damped ringing.
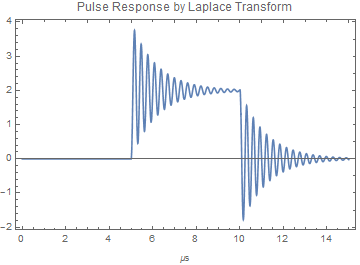
OutputResponse applied to the TransferFunctionModel shows something else. However, when the response is determined by Laplace transform analysis, the expected response is obtained. (And that response agrees with a separate analysis using LTSpice.)
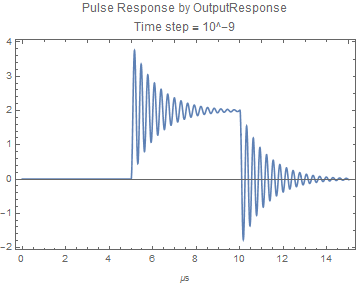
In the discussion on SE, another user suggested the use of an option to OutputResponse which causes it to use NDSolve as a method and allows control of the time step. It is found that as the time step is decreased the output of OutputResponse moves toward agreement with the Laplace method, and at a fine enough step the output becomes identical. The need to verify convergence by just such methods is well known in numerical methods.
The issue I have with this is that in the documentation of OutputResponse there is no mention of this. (At least not that I can find.) There is no mention of it in the Issues section, And there is in fact no section on Options at all. The person who shared this option with me found it by trial and error. Mathematica is producing a wrong result with no warning and no documentation as to how to identify and deal with the problem.
I will be sending this to Wolfram support. If you find this objectionable please join me in doing so.
I attach a notebook which reproduces this problem, and post the graphs below.
 Attachments:
Attachments: