Thinking of ways to do more or less complex interpolations and multiple interpolations at the same time can be this way using the Table command:
x = {{1, 2, 12}, {2, 4, 24}, {3, 8, 38}, {4, 16, 416}, {5, 32, 532}};
y = {{3, 6, 36}, {5, 10, 510}, {7, 14, 714}, {9, 18, 918}, {11, 22,
1122}};
z = {{5, 10, 15}, {10, 15, 20}, {15, 20, 25}, {20, 25, 30}, {25, 30,
35}};
h1 = Table[{FromDigits[Take[FromDigits[Take[x, {m}]], {1}]],
FromDigits[Take[FromDigits[Take[y, {m}]], {1}]],
FromDigits[Take[FromDigits[Take[z, {m}]], {1}]]}, {m, 1,
Count[x, _]}]
(* get {x11,y11,z11},{x21,y21,z21}... *)
h2 = Table[{FromDigits[Take[FromDigits[Take[x, {m}]], {2}]],
FromDigits[Take[FromDigits[Take[y, {m}]], {2}]],
FromDigits[Take[FromDigits[Take[z, {m}]], {2}]]}, {m, 1,
Count[x, _]}]
(* get {x12,y12,z12},{x22,y22,z22}... *)
h3 = Table[{FromDigits[Take[FromDigits[Take[x, {m}]], {3}]],
FromDigits[Take[FromDigits[Take[y, {m}]], {3}]],
FromDigits[Take[FromDigits[Take[z, {m}]], {3}]]}, {m, 1,
Count[x, _]}]
(* get {x13,y13,z13},{x23,y23,z23}... *)
h123 = Table[{FromDigits[Take[FromDigits[Take[x, {m}]], {1}]],
FromDigits[Take[FromDigits[Take[y, {m}]], {2}]],
FromDigits[Take[FromDigits[Take[z, {m}]], {3}]]}, {m, 1,
Count[x, _]}]
(* get {x11,y12,z13},{x21,y22,z23}... *)
h321 = Table[{FromDigits[Take[FromDigits[Take[x, {m}]], {3}]],
FromDigits[Take[FromDigits[Take[y, {m}]], {2}]],
FromDigits[Take[FromDigits[Take[z, {m}]], {1}]]}, {m, 1,
Count[x, _]}]
(* get {x13,y12,z11},{x23,y22,z21}... *)

Or we can change the order of x, y, z by swapping the letters within the code:
hzyx = Table[{FromDigits[Take[FromDigits[Take[z, {m}]], {1}]],
FromDigits[Take[FromDigits[Take[y, {m}]], {1}]],
FromDigits[Take[FromDigits[Take[x, {m}]], {1}]]}, {m, 1,
Count[x, _]}]
(* get {z11,y11,x11},{z21,y21,x21}... *)
hyzx = Table[{FromDigits[Take[FromDigits[Take[y, {m}]], {1}]],
FromDigits[Take[FromDigits[Take[z, {m}]], {1}]],
FromDigits[Take[FromDigits[Take[x, {m}]], {1}]]}, {m, 1,
Count[x, _]}]
(* get {y11,z11,x11},{y21,z21,x21}... *)

Or even interpolate by doing both things, swapping x, y, z and positions simultaneously:
hy2z3x1 =
Table[{FromDigits[Take[FromDigits[Take[y, {m}]], {2}]],
FromDigits[Take[FromDigits[Take[z, {m}]], {3}]],
FromDigits[Take[FromDigits[Take[x, {m}]], {1}]]}, {m, 1,
Count[x, _]}]
(* get {y12,z13,x11},{y22,z23,x21}... *)
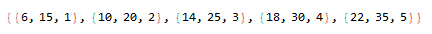
These are just a way to do multiple simultaneous interpolations, if anyone knows how to do this using faster or shorter codes can help in this topic? Thanks.