Message Boards Message Boards

Create custom component with custom formula or transfer function?

Lakshmi Rajagopalan
Posted 5 years ago

How can I create a custom component with custom equation of transfer function? I have an equation for a low pass filter as shown below

L(t)= exp(-t/tau)/tau

Thanks
POSTED BY: Lakshmi Rajagopalan
10 Replies
Sort By:

Thank you very much Neil Lakshmi
POSTED BY: Lakshmi Rajagopalan

Lakshmi,

You confused me because TransferFunctionModel takes a frequency domain expression and your expression looked like a frequency domain expression because time was called "s" (which is usually reserved for the complex variable in Laplace Transforms).

You should do this

exp = E^(-t/\[Tau])/\[Tau]
CreateSystemModel["myFilter", 
 TransferFunctionModel[Simplify[LaplaceTransform[exp, t, s]], s]]

Regards,

Neil
POSTED BY: Neil Singer

Lakshmi,

To be clear, The model looks like this:

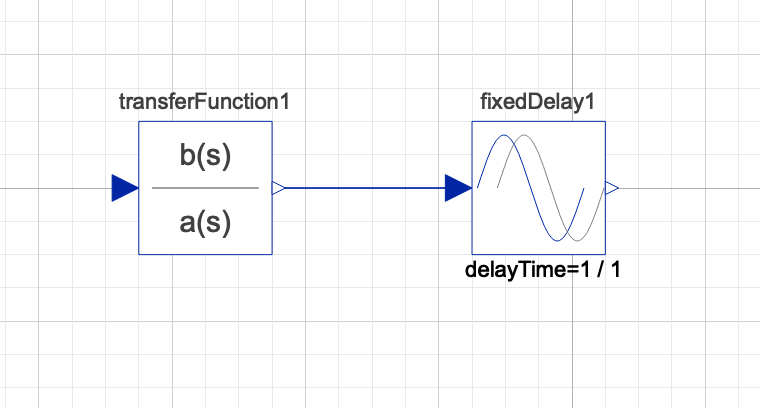
enter image description here

and the code is

model example
  Modelica.Blocks.Continuous.TransferFunction transferFunction1(a = {1, 0}, b = {0, 1}) annotation(Placement(visible = true, transformation(origin = {-55, 0}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
  Modelica.Blocks.Nonlinear.FixedDelay fixedDelay1(delayTime = 1 / 1) annotation(Placement(visible = true, transformation(origin = {-5, 0}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
equation
  connect(transferFunction1.y, fixedDelay1.u) annotation(Line(visible = true, origin = {-30.5, 0}, points = {{-13.5, 0}, {13.5, 0}}, color = {1, 37, 163}));
  annotation(Diagram(coordinateSystem(extent = {{-150, -90}, {150, 90}}, preserveAspectRatio = true, initialScale = 0.1, grid = {5, 5})), Icon(coordinateSystem(extent = {{-100, -100}, {100, 100}}, preserveAspectRatio = true, initialScale = 0.1, grid = {10, 10}), graphics = {Rectangle(visible = true, lineColor = {0, 114, 195}, fillColor = {255, 255, 255}, extent = {{-100, -100}, {100, 100}}, radius = 25), Text(visible = true, textColor = {64, 64, 64}, extent = {{-150, 110}, {150, 150}}, textString = "%name")}));
end example;

The fixed delay is your exponent term.

Regards
POSTED BY: Neil Singer

Lakshmi,

You have a few issues.

  1. Your system is a time delayed system (it has a transportation lag). This system cannot be represented with a transfer function Model in modelica because it is not a polynomial transfer function.

  2. You can make the correct system as a transfer function of 1/s and a time delay (e^-(tau*s)). The time delay is tau in this example but see my point 3 below.

  3. you wrote e^-s/tau are you sure this is correct? In your case your time delay is 1/tau -- did you intend that? or did you intend a time delay of tau seconds?

  4. You can construct your model in WSM or you can construct the model in WMA by "wiring" the blocks together to form the model described above using CreateSystemModel to create the model.

Regards,

Neil
POSTED BY: Neil Singer

Hi Neil, Thanks for your response. I have 2 variables in the function. One is tau and other is "s". What i am trying to build is a standard equation describing the impulse response of a low pass filter with time constant tau. I want to use this as my filter in system modeler.

Ltau(s)= [Exp(-s/?au)]/ ?au where Ltau is a function of time (s) and tau is my time constant

Please find attached picture of the WMA script and output. enter image description here

Thanks Lakshmi
POSTED BY: Lakshmi Rajagopalan
Updating Name
Updating Name
Posted 5 years ago

Lakshmi,

I’m confused. You refer to this as your transfer function and use it that way in the “TransferFunction” command in the way you would specify a frequency domain expression. However, now you say it’s a function of time. Is your expression an impulse response in time and not a transfer function in frequency ?

Regards,

Neil
POSTED BY: Updating Name

Hi, Ltau(s) is a function of time, and tau is the time constant. Its the impulse response of an IIR filter. I recently started learning Mathematica and system modeler. I thought the appropriate component in blocks to do this would be a transfer function or a first order filter. Please let me know

Thanks Lakshmi
POSTED BY: Lakshmi Rajagopalan

Hi, Thank you. I created this transfer function using CreateSystemModel 

RTFV2= CreateSystemModel[TransferFunctionModel[{{{E^(-s/\[Tau])}}, \[Tau]}, s]]

but when I used it in system model it gives me an error that there is no scope for variable s. Alternatively, I also tried to modify the in-built transfer function in modelica but was not sure how to use the exponent. What is the equation of y? Please let me know. Lakshmi
POSTED BY: Lakshmi Rajagopalan

Lakshmi,

You can also implement your transfer function using a continuous "TransferFuntion" block. In your example, you would also need a FixedDelay to handle the transportation lag e(-t *s) in the numerator.

Regards,

Neil
POSTED BY: Neil Singer

Hi Lakshmi,

You can check out the following videos in Wolfram U on creating custom components in SystemModeler. https://www.wolfram.com/wolfram-u/modeling-systems/

If you are interested in creating your component in Mathematica, see the documentation on CreateSystemModel here: https://reference.wolfram.com/language/ref/CreateSystemModel.html

Thanks, Ankit
POSTED BY: Ankit Naik
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard

Group Abstract Group Abstract