Imbalance data occurs when some types of data distribution dominate the instance space compared to other data distributions (He et. al., 2008). It happens frequently in financial fraud data. Using an imbalance dataset in training may result in misleading conclusions for anomaly detection as ML algorithms tend to show bias for the majority class.

One common way to deal with imbalance datasets is using oversampling methods such as SMOTE. He et. al. (2008), instead, introduce an adaptive method that outperforms SMOTE in many cases, at the same time, does not require hypothesis evaluation for generating synthetic data and thus more efficient.

The detailed algorithm and introduction can be found in their paper: https://sci2s.ugr.es/keel/pdf/algorithm/congreso/2008-He-ieee.pdf

I build-up a function for data pre-processing using this ADASYN method:

adasyn[input_, minorClass_, majorClass_, \[Beta]_, K_] :=
 Module[
  {g, m, ms, ml , sinput, linput, r, s, rn, xx, delta},
  ms = Count[Values[input], minorClass];
  ml = Count[Values[input], majorClass];
  m = ms + ml;
  sinput = input[[Flatten[Position[Values[input], minorClass]]]];
  linput = input[[Flatten[Position[Values[input], majorClass]]]];
  xx = ConstantArray[Null, {ms, K}];
  delta = ConstantArray[Null, ms];
  g = ConstantArray[Null, ms];
  r = ConstantArray[Null, ms];
  s = ConstantArray[Null, ms];
  rn = ConstantArray[Null, ms];

  For [i = 1, i <= ms, i++,
   xx[[i]] = 
    Nearest[Flatten[{Keys[input], Delete[Keys[sinput], i]}], 
      Keys[sinput][[i]] , K] // Flatten; 
   delta[[i]] = 
    Length[Position[Keys[linput], Alternatives @@ xx[[i]]]]; 
   r[[i]] = delta[[i]]/K];

  For[i = 1, i <= ms, i++,
   rn[[i]] = r[[i]]/Total[r];
   g[[i]] = rn[[i]]* (ml - ms)*\[Beta] // Ceiling;
   s = ReplacePart[s, i -> ConstantArray[Null, g[[i]]]];
   For [z = 1, z <= g[[i]], z++,
    s[[i, z]] = 
     Keys[sinput][[
        i]] + (RandomSample[xx[[i]], 1] - Keys[sinput][[i]])*
        RandomReal[] /. {x_} -> x
    ]
   ];

  s
  ]

I'm not proficient in mathematica coding and those for loops might be able to optimized in many ways.

This is a very preliminary version that allows for only one key, one minority class. More functionalities can be added further, such as for multiple datas (keys), multiple classes (values).

Package imbalanced-learn in Python has adopted ADASYN and SMOTE methods. Hope mathematica can add this functionality in the near future.

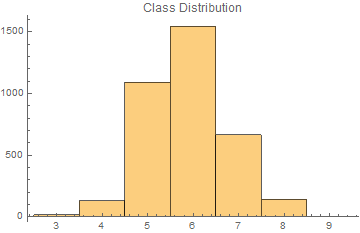
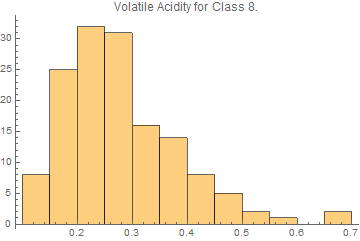
Update: I test the function using Wine Quality example data from Wolfram. Volatile Acidity is the only data selected, and Class 8. are selected as minority in comparison to the majority Class 6.

data = ExampleData[{"MachineLearning", "WineQuality"}, "TrainingData"];
Histogram[Values[data], PlotLabel -> "Class Distribution"]

Histogram[
 Keys[data][[Flatten[Position[Values[data], 8.]]]][[All, 2]], 
 PlotLabel -> "Volatile Acidity for Class 8."]

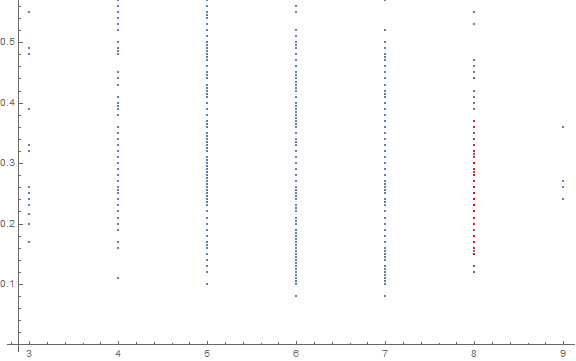
selectedkey = Keys[data][[All, 2]];
selectedata = Thread[selectedkey -> Values[data]];
ada = Thread[Flatten[adasyn[selectedata, 8., 6., 1, 5]] -> 8.];
ListPlot[{Transpose[{Values[#1], Keys[#1]}], 
    Transpose[{Values[#2], Keys[#2]}]}, 
   PlotStyle -> {Automatic, {Red, Opacity[0.05]}}, 
   ImageSize -> Large] &[selectedata, ada]

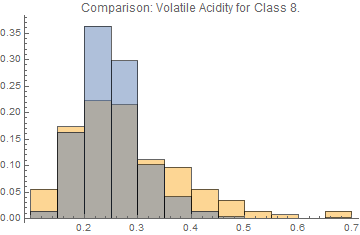
Histogram[{Keys[data][[Flatten[Position[Values[data], 8.]]]][[All, 
    2]], Keys[ada]}, 10, "Probability", 
 PlotLabel -> "Comparison: Volatile Acidity for Class 8."]

Histogram[{Values[selectedata], Values[ada]}, 
 PlotLabel -> "Class Disbtibution before and after ADASYN"]

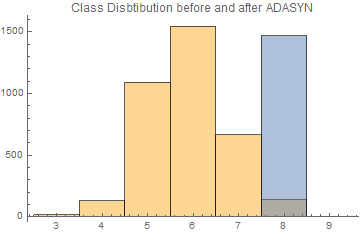
The data of the minority class, which is Class 8. in my case, after ADASYN adjustment seems to be more concentrate though.