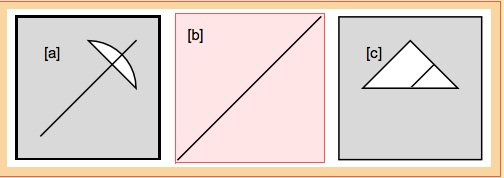
Im trying to create a difference region by finding the difference between a rectangle and a crescent shape (fig. [a]) created by modifying Bezier data for a circle. The crescent is a polygon based on points created with BezierFunction[]. The goal is to use the difference region to mask out images of lines such as the diagonal where it extends beyond the border of the crescent in figure [a]. In a previous project, I was successful with RegionDifference[rectangle, disc] and RegionDifference[polygon, polygon] using simple polygons defined by three and four points as in figure [c], but using the crescent polygon as a region I fail with RegionDifference[polygon, polygon] and RegionDifference[polygon, rectangle] with the arguments in any order. Figure [b] provides an example. The error message is
{RegionDifference[Polygon[(
)],Polygon[(<<1>>)]]} is not a valid region to plot. >>
It seems that RegionDifference[] does not accept the list of points for the crescent as the basis for a valid Polygon[] region. The list appears to be uncomplicated. I would like to know why and find a solution.
Mathematica 10.0.0.0 OS 10.9.5
sz = 1.5; (* rect corner dimension *)
c = 0.551915024494; (* Bezier constant for circle *)
bz = {{0, 1}, {c, 1}, {1, c}, {1, 0}}; (* Bezier control points *)
bzF = BezierFunction[bz];
bzFPts = Table[bzF[t], {t, 0, 1, .1}];
crescentPts = AppendTo[bzFPts, bzFPts[[1]]];
(* illustrate the crescent with figure and ground
but without RegionDifference[] *)
crescentPolygon = {EdgeForm@Black, FaceForm@White,
Polygon[crescentPts]};
background = {EdgeForm@Black, FaceForm@LightGray,
Rectangle[{-sz, -sz}, {sz, sz}]};
figure = Line[{{-1, -1}, {1, 1}}];
g1 = Graphics[{background, crescentPolygon, figure,
Text["[a]", {-.75, .75}]}, ImageSize -> {100, 100}];
(* RegionDifference between gray background and white crescent *)
rectanglePts = {{-sz, -sz}, {-sz, sz}, {sz,
sz}, {sz, -sz}, {-sz, -sz}};
regionDiffCrescent = First@RegionPlot@RegionDifference[
Polygon@rectanglePts,
Polygon@crescentPts
];
(* remove the default directives from new region *)
maskCrescent = DeleteCases[regionDiffCrescent, _Directive, -1];
g2 = Graphics[{figure, FaceForm@LightGray, maskCrescent,
Text["[b]", {-.75, .75}]},
ImageSize -> {100, 100}];
(* region diff with triangle works properly *)
regionDiffTriangle = First@RegionPlot@RegionDifference[
Polygon@rectanglePts,
Polygon@{{-1, 0}, {0, 1}, {1, 0}, {-1, 0}}];
maskTriangle = DeleteCases[regionDiffTriangle, _Directive, -1];
g3 = Graphics[{figure, FaceForm@LightGray, maskTriangle,
Text["[c]", {-.75, .75}]},
ImageSize -> {100, 100}];
Show[GraphicsRow[{g1, g2, g3}, Background -> White]]