Dear members of Wolfram community!
I have one mathematical problem from an area of structural inorganic chemistry. Short introduction: anions [TiF6]2- are simple octahedral units, that can associate with each other forming more complex anionic units by sharing vertexes or edges of octahedra. Thus, in the case of two octahedra there are two variants of connection - by sharing one vertex and by sharing one edge (because of symmetry, vertexes and edges of single octahedron are indistinguishable).
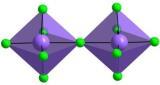
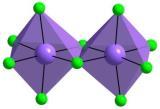
Now, let's consider the case of
sharing vertexes only. Three octahedra can be joined by three variants: three octahedra in a line, three octahedra forming right angle and three octahedra forming a planar ring (circular combinations are also possible).
In the case of four octahedra additional dimension appears (3D) and if I have calculated right, there are 10 variants of their combination (by sharing vertexes only).
On the basis of this information I try to develop an algorithm, by which one can calculate the number of possible combinations of
n octahedra (for the beginning by only vertex sharing), and I need your help to do this.
Thank you in advance,
Igor.