Group Abstract Group Abstract

Message Boards Message Boards

Compile to find digits ratio of integers composed by sequential numbers?

Hello community, I'm trying to optimize the speed of a code using Parallelize and Compile but I'm not having very expressive results (I'm still inexperienced in these commands). I believe that I am using these commands in an inefficient way (my attempt is at the end of the post)... below is explained where is the problem for my case in detail. First I'll explain the context of my question and then explain what I want to do.

Taking the table of the following numbers for example:

z = 5;
FromDigits[Table[10^x - 1, {x, {Range[z]}}]]

ima1

I then transformed into integers composed of sequential numbers as follows:

z = 2;
FromDigits[Table[10^x - 1, {x, {Range[z]}}]]
g[k_] := (ToExpression[
    StringDelete[
     ToString[Table[i, {i, Range[k]}]], {"{", "}", " ", ","}]]);
Table[g[j1], {j1, FromDigits[Table[10^x - 1, {x, {Range[z]}}]]}]

ima2

To count the different digits of each of these numbers:

z = 6;
g[k_] := (DigitCount[
    ToExpression[
     StringDelete[
      ToString[Table[i, {i, Range[k]}]], {"{", "}", " ", ","}]]]);
Table[Print[g[j1]], {j1, 
  FromDigits[Table[10^x - 1, {x, {Range[z]}}]]}]

ima3

And finally, make a relationship (ratio) between the number of digits ´0´ (which is less than any other digit) and another digit (e.g. ´2´):

z = 6;
g[j_, h_] := (Take[
    DigitCount[
     ToExpression[
      StringDelete[
       ToString[Table[i, {i, 1, j}]], {"{", "}", " ", ","}]]], {h}]);
Table[g[k1, 10], {k1, FromDigits[Table[10^x - 1, {x, {Range[z]}}]]}]
Table[g[k2, 2], {k2, FromDigits[Table[10^x - 1, {x, {Range[z]}}]]}]
Table[g[k3, 10]/g[k3, 2], {k3, 
  FromDigits[Table[10^x - 1, {x, {Range[z]}}]]}]
Table[N[g[k4, 10]/g[k4, 2], 11], {k4, 
  FromDigits[Table[10^x - 1, {x, {Range[z]}}]]}]

ima4

The largest number of terms I can calculate is 8 before it crashes (?!) the program. Below the result obtained for 8 terms without using Parallelize or Compile:

EvaluationData[z = 8;
 a = FromDigits[Table[10^x - 1, {x, {Range[z]}}]];
 g[j_, h_] := (Take[
    DigitCount[
     ToExpression[
      StringDelete[
       ToString[Table[i, {i, 1, j}]], {"{", "}", " ", ","}]]], {h}]);
 b = Flatten[Table[N[g[k4, 10]/g[k4, 2], 11], {k4, a}]];
 {ListLinePlot[b, 
   PlotRange -> {{1, Automatic}, {Automatic, Automatic}}, 
   LabelingFunction -> (#1 &), ImageSize -> Large], b}]

ima5

Using the result data I can make an estimate of the equation governing these fractions based on experimental (result made only by observing the first 8 terms; by guessing) and also test the value of the guessed equation at the infinite limit:

u: {1,2,3,4,5,6,7,8}

num = numerator: {0,9,189,2889,38889,488889,5888889,68888889}

dem = denominator: {1,20,300,4000,50000,600000,7000000,80000000}

z = 8;
num = (10 - 10^(1 + u) + 9*u*10^u)/90
dem = u*10^(u - 1)
sim = Simplify[num/dem]
Table[N[(-10 + 10^(1 - u) + 9*u)/(9*u), 11], {u, Range[z]}]

Limit[sim, u -> \[Infinity]]

ima6

  • My attempt using Compile and Parallelize:

Now comes my attempt to improve the initial code using Parallelize and Compile to get the dots (experimental) with a better timing. I would like to be able to calculate faster and more points using the experimental code to check the data in the guessed equation. But I did not get a much better result due to my lack of experience using these commands...my attempt:

z = 8;
g = Compile[{{x, _Integer}}, Range[10^x - 1]]
EvaluationData[
 Parallelize[
  h[x1_] := (DigitCount[
     ToExpression[
      StringDelete[ToString[g[x1]], {"{", "}", " ", ","}]]])];
 b = Flatten[
   Table[N[Take[h[i], {10}]/Take[h[i], {2}], 11], {i, Range[z]}]];
 {ListLinePlot[b, 
   PlotRange -> {{1, Automatic}, {Automatic, Automatic}}, 
   LabelingFunction -> (#1 &), ImageSize -> Large], b}]

ima7

  • My question:

There was no significant improvement in computing time (approx. 10%) and I believe that discrete improvement was due to Parallelize and not to Compile. How do I use these commands to optimize this code and make it faster (or lighter..?)?? For I believe I did not know how to use them properly in the best way....

Thanks.
POSTED BY: Claudio Chaib
6 Replies
Sort By:

Hello, I managed to improve the time to find the sum of the digits of each type in this sequence of numbers… My new result was 1/24 of the time of my best previous result (!), but I would like to know if anyone knows a method that makes it even better..? ... I would like a method that could sum the digits without creating an effective table ( because when a table is generated, the entire table is stored in memory, the best way would be something like While?! ), so that instead of creating a table the code would successively summing the digits "forgetting" the previous results for better performance... Please, if anyone knows a way to increase the sum of digits function in a more efficient way can you help me?

My new result:

f1[z_] := 
 Module[{k, x}, 
  N[Table[Last@
      Accumulate@
       ParallelTable[Count[IntegerDigits[x], 0], {x, 1, 10^k - 1}]/
     Last@Accumulate@
       ParallelTable[
        Count[IntegerDigits[x], 2], {x, 1, 10^k - 1}], {k, Range[z]}],
    11]]
ListLinePlot[f1[7], 
  PlotRange -> {{1, Automatic}, {Automatic, Automatic}}, 
  LabelingFunction -> (#1 &), ImageSize -> Large] // AbsoluteTiming

imag1

Thanks.
POSTED BY: Claudio Chaib

Could change Last@Accumulate@ParallelTable to Sum and that should keep memory consumption down.
POSTED BY: Daniel Lichtblau

Thank you very much Daniel... I was complicating the way to do it, but you reminded me that the simplest way is even better! I just switched Sum by ParallelSum and the result was: 1.045 seconds (66% of the previous time) and the memory improved even more..! 

f1[z_] := 
 Module[{k, x}, 
  N[Table[ParallelSum[Count[IntegerDigits[x], 0], {x, 1, 10^k - 1}]/
     ParallelSum[Count[IntegerDigits[x], 2], {x, 1, 10^k - 1}], {k, 
     Range[z]}], 11]]
ListLinePlot[f1[7], 
  PlotRange -> {{1, Automatic}, {Automatic, Automatic}}, 
  LabelingFunction -> (#1 &), ImageSize -> Large] // AbsoluteTiming

Thanks.
POSTED BY: Claudio Chaib

Hi again. I still have some doubts... I tried to elaborate a new code (...but maybe has a better way using some increment in counting the digits that I do not know to do...). Also have doubts in the commands Parallelize and Compile, which in some cases did not work as I wanted... Below are the versions of the codes that I did compare:

This is my old code that had the problem of the big numbers (creating a big number to then count the digits), just to be able to compare (absolute timing) with my new code (using 7 terms in all comparisons below):

z = 7;
g = Compile[{{x, _Integer}}, Range[10^x - 1]]
EvaluationData[
 Parallelize[
  h[x1_] := (DigitCount[
     ToExpression[
      StringDelete[ToString[g[x1]], {"{", "}", " ", ","}]]])];
 b = Flatten[
   Table[N[Take[h[i], {10}]/Take[h[i], {2}], 11], {i, Range[z]}]];
 {ListLinePlot[b, 
   PlotRange -> {{1, Automatic}, {Automatic, Automatic}}, 
   LabelingFunction -> (#1 &), ImageSize -> Large], b}]

i0

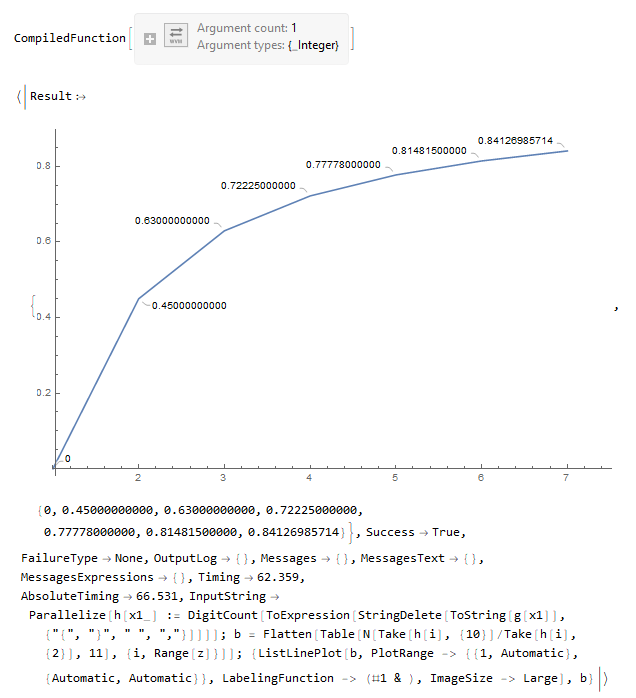
This (below) is the new code I developed, it makes the sum of the digits without have to generate a large number before it (again, I don't know if it was the best way to do this..). The memory problem has apparently been solved but it has shown slower than the old code when evaluate(?!). And Parallelize wasn't very efficient either, I still don't know why (?!). Doing two variations of this code, one with and one without the Parallelize command did not change almost nothing in absolute timming ..of course if I did that correctly... (at least it does not crash the PC with lack of memory due to premature big numbers). My new code:

n = 7;
z = Compile[{{k, _Integer}}, 10^k - 1]
EvaluationData[
 Parallelize[b = Table[Sum[DigitCount[x], {x, 1, z[i]}], {i, 1, n}]];
 c = Table[
   N[FromDigits[
     Take[FromDigits[Take[b, {v}]], {10}]/
      Take[FromDigits[Take[b, {v}]], {2}]], 11], {v, 1, n}];
 {ListLinePlot[c, 
   PlotRange -> {{1, Automatic}, {Automatic, Automatic}}, 
   LabelingFunction -> (#1 &), ImageSize -> Large], c}]

i1

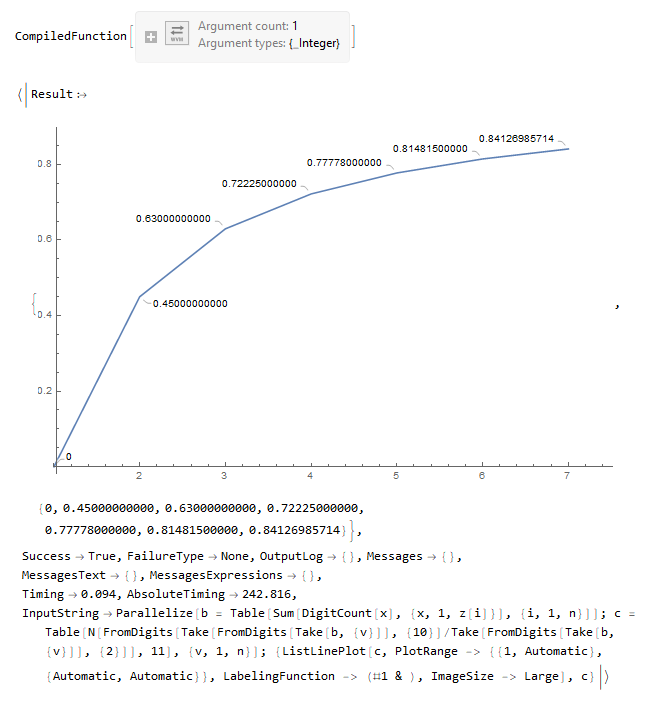
This version below of the code proved to be better, also does not have the problem of the large numbers that my old version had and is faster, but is not in a form as automatic as the version containing Table (above)... But Parallelize seems to work in this case (the absolute timing was almost 1/2 from the time of my old code and went to almost 1/6 of the absolute timing of the new version with Table)! I do not know why Parallelize worked with several “manual” lines and practically did not work in the version of this code with Table (?!).

z = Compile[{{k, _Integer}}, 10^k - 1]
EvaluationData[Parallelize[b1 = Sum[DigitCount[x], {x, 1, z[1]}];
  b2 = Sum[DigitCount[x], {x, 1, z[2]}];
  b3 = Sum[DigitCount[x], {x, 1, z[3]}];
  b4 = Sum[DigitCount[x], {x, 1, z[4]}];
  b5 = Sum[DigitCount[x], {x, 1, z[5]}];
  b6 = Sum[DigitCount[x], {x, 1, z[6]}];
  b7 = Sum[DigitCount[x], {x, 1, z[7]}];
  c1 = N[FromDigits[Take[b1, {10}]/Take[b1, {2}]], 11];
  c2 = N[FromDigits[Take[b2, {10}]/Take[b2, {2}]], 11];
  c3 = N[FromDigits[Take[b3, {10}]/Take[b3, {2}]], 11];
  c4 = N[FromDigits[Take[b4, {10}]/Take[b4, {2}]], 11];
  c5 = N[FromDigits[Take[b5, {10}]/Take[b5, {2}]], 11];
  c6 = N[FromDigits[Take[b6, {10}]/Take[b6, {2}]], 11];
  c7 = N[FromDigits[Take[b7, {10}]/Take[b7, {2}]], 11]];
 d = {c1, c2, c3, c4, c5, c6, c7};
 {ListLinePlot[d, 
   PlotRange -> {{1, Automatic}, {Automatic, Automatic}}, 
   LabelingFunction -> (#1 &), ImageSize -> Large], d}]

i3

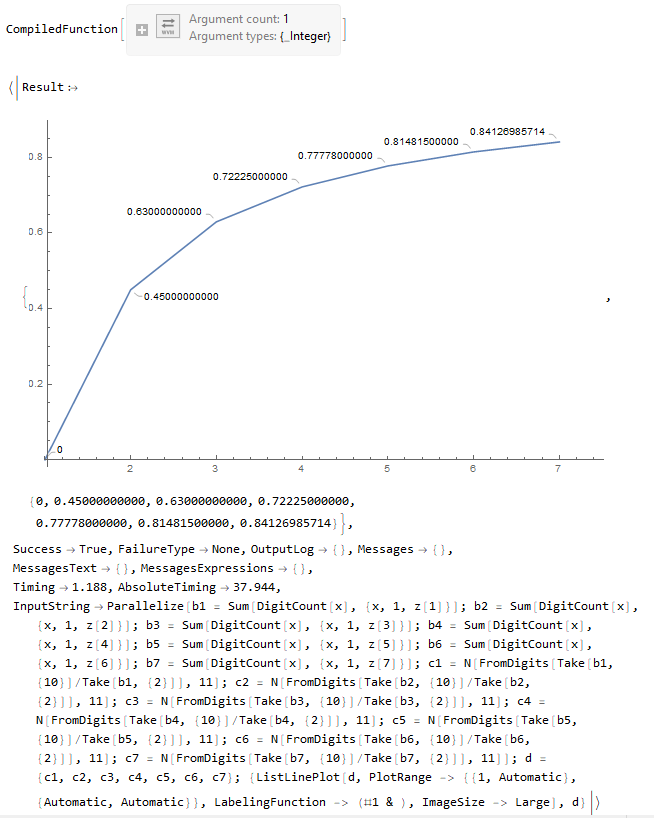
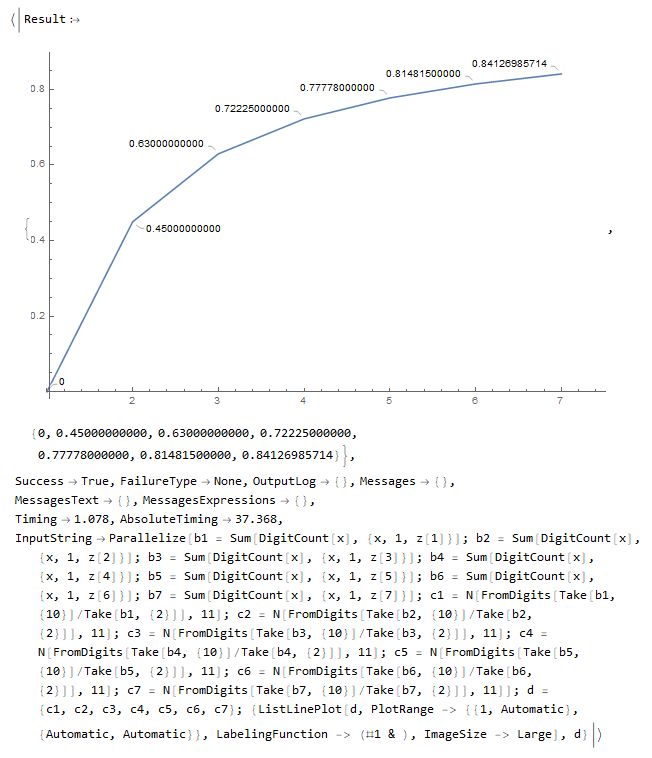
This below is the same code as the above but without using Compile... with the Compile command I didn't know how to took advantage in none of the tested cases so far, because it hasn't changed anything when I made variations of the codes with or without it. How do I use Compile to help solve my problem? Or in this type of problem it has not much use? Same code as the previous one without Compile:

z[k_] := (10^k - 1)
EvaluationData[Parallelize[b1 = Sum[DigitCount[x], {x, 1, z[1]}];
  b2 = Sum[DigitCount[x], {x, 1, z[2]}]; 
  b3 = Sum[DigitCount[x], {x, 1, z[3]}]; 
  b4 = Sum[DigitCount[x], {x, 1, z[4]}]; 
  b5 = Sum[DigitCount[x], {x, 1, z[5]}]; 
  b6 = Sum[DigitCount[x], {x, 1, z[6]}]; 
  b7 = Sum[DigitCount[x], {x, 1, z[7]}]; 
  c1 = N[FromDigits[Take[b1, {10}]/Take[b1, {2}]], 11]; 
  c2 = N[FromDigits[Take[b2, {10}]/Take[b2, {2}]], 11]; 
  c3 = N[FromDigits[Take[b3, {10}]/Take[b3, {2}]], 11]; 
  c4 = N[FromDigits[Take[b4, {10}]/Take[b4, {2}]], 11]; 
  c5 = N[FromDigits[Take[b5, {10}]/Take[b5, {2}]], 11]; 
  c6 = N[FromDigits[Take[b6, {10}]/Take[b6, {2}]], 11]; 
  c7 = N[FromDigits[Take[b7, {10}]/Take[b7, {2}]], 11]];
 d = {c1, c2, c3, c4, c5, c6, c7};
 {ListLinePlot[d, 
   PlotRange -> {{1, Automatic}, {Automatic, Automatic}}, 
   LabelingFunction -> (#1 &), ImageSize -> Large], d}]

i4

I know I need to learn a lot about these functions (Parallelize, Compile, etc) but if anyone can give a feedback of what I'm doing wrong or some hint of how I can do better I would be very grateful..!

Thank you very much!
POSTED BY: Claudio Chaib

Compile will only work with machine integers at this time. If ever it gets extended to work with bignums, the issue might stll be that the library code is bogged down handling large numbers. But it seems like excess to create these huge values to begin with. Could instead just iterate to 10^k-1 for whatever k, incrementing counts for each digit's appearances as you go. That is to say, when you encounter 32141, say, each counter for 2,3,4 gets increased by 1, and the counter for 1 gets increased by 2.
POSTED BY: Daniel Lichtblau

Thanks for the reply Daniel, I think I understand what you're telling me... Instead of counting the digits of the whole number I can count each part before joining, since the total sum of the digits are significantly smaller numbers... I will try to advance the count in the equation to a more initial position in it without having to create large numbers.
POSTED BY: Claudio Chaib
Reply to this discussion
Community posts can be styled and formatted using the Markdown syntax.
Tag limit exceeded
Note: Only the first five people you tag will receive an email notification; the other tagged names will appear as links to their profiles.
Reply Preview
Attachments
Remove
or Discard