I believe it's very unlikely that you could solve this system symbolically... I may be mistaken but see:
If you take the equation 1 and solve for x0 you have a very large solutions (which should be subsequently equated with the equation 2, also solved to x0, to then solve a definitive x1 equation). Look at equation 1 solved for "x0":
Solve[p1*a1*(-x0 + (e1b + e1l - x1)*a1)^(-2) +
p2*a2*((e1b + e1l - x1)*a2)^(-2) == (w0l +
x0*P00 - (e1b - x1)*P01)^(-2)*P01, {x0}] // InputForm

If you observe this solution in Word with Arial font and size 9, you will see that it gives 119 pages only to the symbolic solution of equation 1 for "x0":
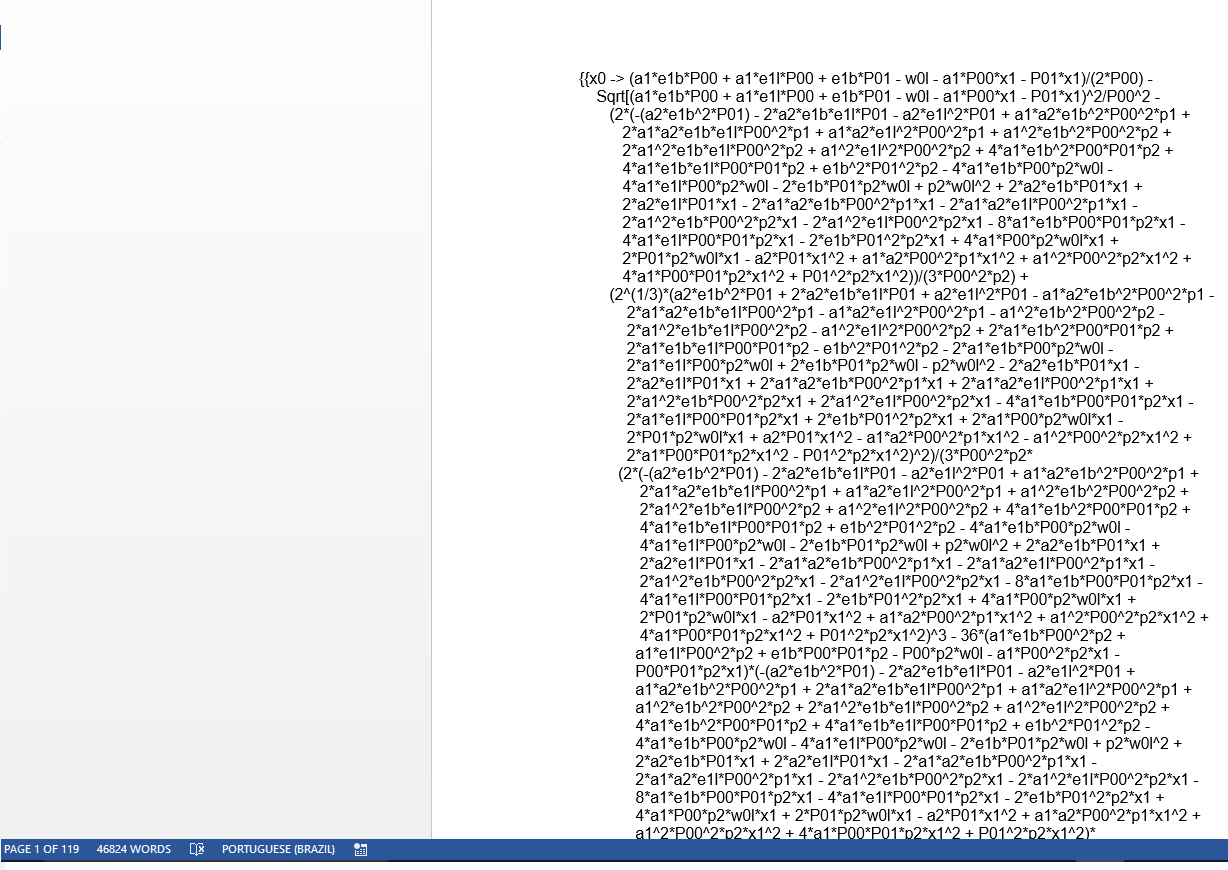
Then you would still have to isolate the x0 in equation 2 to match these solutions and solve an even more complex equation later...!
You may solve this system if you have fewer variables and more numeric values in some (many) of the positions... At least that's what I believe...