I need to cut an ellipse given by the inverse FishIM of its weight matrix, and its centre. Here are two examples of matrices, "Good" and "Bad", with various charcteristics (excentricity, length, etc).

Centre = {5.\
1800354591485186774027741688510520464782714191942012290756`29.\
825575763955253, 
   6.7652867417413797504838000079634290004451979804037147988214`29.\
825575763955253};

Good = {{0.5879689788535514100187639228053951611316223513920108533286`\
29.524545768291276, 
    0.2714648412202274168105922143507295745810643233824377825774`30.\
137549484531476}, \
{0.2714648412202274168105922143507295745810643233824377825774`30.\
137549484531476, 
    0.1520210894667726296750459918758147306490376981723983877731`29.\
56407044570504}};
Bad = {{0.4219874795337851353296839707215259074013647925209521994819`\
29.635459593034348, 
    0.3573032974632832507786050335185528535518963368910542495894`30.\
1919939283046}, \
{0.3573032974632832507786050335185528535518963368910542495894`30.\
1919939283046, 
    0.3497045407408659806173023708108825260219718227402179654922`29.\
577952677191043}};



FishIM = Good;

Print["Information matrix : ", MatrixForm[FishIM]];  
{a, b} = Sqrt[
 1/Eigenvalues@FishIM]; (* racines de VP de \[CapitalSigma]^-1  *)
Print[Style["{a,b}=", "Section"], {a, b}];

{Va, Vb} = Eigenvectors@FishIM;
\[Theta] = Min[ArcCos[{-1, 0}.Va], ArcCos[{-1, 0}.(-Va)]];
circ = N[\[Pi] (a + b)  Hypergeometric2F1[-1/2, -1/2, 1, 
    h]]; (* Gauss-Kummer formula  *)
Gr = {};
excentricité := Sqrt[1 - Min[a, b]^2/Max[a, b]^2];  (*  Mathworld  *)

h := ((a - b)/(a + b))^2;
y[x_] := b/a Sqrt[a^2 - x^2];
Print["Excentricité de l'ellipse: ", N@excentricité];
Print["Circonférence (Gauss-Kummer): ", circ, 
  " Numerical approximation : ", 
  2 N[ArcLength[{t, y[t]}, {t, -a, a}], Chif]];

Print["surface Théorique: ", N[\[Pi] a b ]];
Print@Graphics[{LightGreen, Ellipsoid[Centre, {a, b}]}, Frame -> True];
Print["surface 1: ", N@RegionMeasure[Ellipsoid[Centre, {a, b}]]];
Print@Graphics[{LightRed, Ellipsoid[Centre, Inverse@FishIM]}, 
   Frame -> True];
Print["surface 2: ", 
  N@RegionMeasure[Ellipsoid[Centre, Inverse@FishIM]]];
EllipsRef = 
 Show[Graphics[{LightGray, Ellipsoid[Centre, Inverse@FishIM]}],  
  ParametricPlot[
   Centre + RotationMatrix[\[Theta]].{t, y[t]}, {t, -a, a}, 
   PlotRange -> All, PlotPoints -> 100
   , AspectRatio -> Automatic], 
  ParametricPlot[
   Centre + RotationMatrix[\[Theta]].{t, -y[t]}, {t, -a, a}, 
   PlotRange -> All, PlotPoints -> 100
   , AspectRatio -> Automatic], 
  Graphics[{PointSize@Large, 
    Point[Centre + RotationMatrix[\[Theta]].{-a, 0}]}], 
  Graphics[{PointSize@Large, Yellow, Point[Centre]}], 
  ImageSize -> Large]

I wrote this routine to do the job for a centered ellipse:

Chif = 30(*$MachinePrecision*);

TourCir[np_, a_, b_, \[Theta]_, circ_] := 
  Block[{X, pred, sol, x, EchEllP, EchEllM, Angles, k, r, eq, u},
   eq[u_] := b/a Sqrt[a^2 - u^2];
   X = {};
   pred = -(a + 0.001);
   Do[
    sol = 
     NMinimize[{(SetPrecision[
           ArcLength[
            RotationMatrix[\[Theta]].({t, eq[t]}), {t, -a, u}], 
           Chif] - SetPrecision[k  circ/(np), Chif])^2, 
       a > u > Max[-a, pred]}, {u}, WorkingPrecision -> Chif];

    Print["Verification lengths: ", 
     np  ArcLength[
        RotationMatrix[\[Theta]].({t, eq[t]}), {t, -a, 
         u /. Last@sol}]/circ, " =?= k=", k];

    Print@Chop@sol;
    pred = u /. Last@sol;
    AppendTo[X, Chop@pred]
    , {k, np/2}];
   Print["Dim X=", Dimensions@X];
   Print["X=", X];
   EchEllP = Map[{#, eq[#]} &, X];
   EchEllM = Map[-{#, eq[#]} &, X];
   Print["Dim EchEll=", Dimensions@EchEllP];
   Print@ListPlot[MapAll[Re, Join[EchEllP, EchEllM]], 
     PlotRange -> All, PlotLabel -> "Solutions"];
   MapAll[Re, Join[EchEllP, EchEllM]]
             ];

Parameters: np is half the number of points, a is a eigenvalue of the ellipse a teta is the angle made by the corresponding eigenvector and the vector {-1,0}. From a and teta, we obtain the initial (and arbitrary) point on the ellipse. You already guessed that everything's fine with the Good ellipse: here are the initial point (black), and the centre: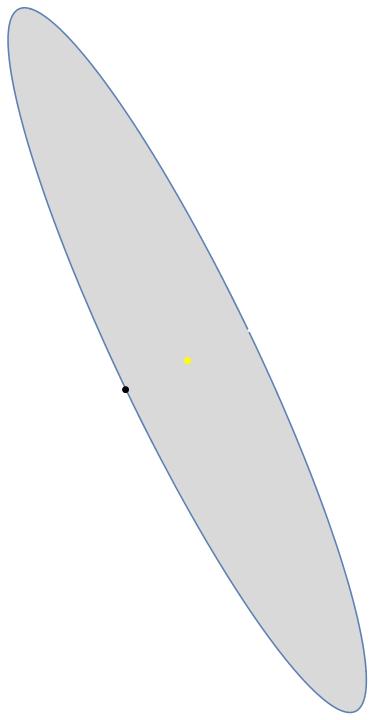

Here is the final result (np=4):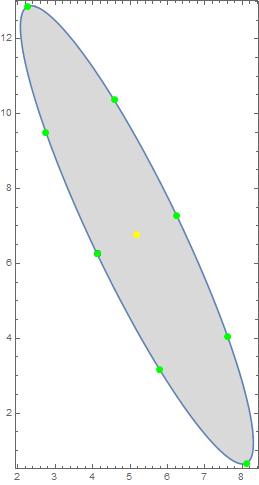

There is in the routine a verification instruction: the curvilinear abcissa associted with the k th point shoul be k;

Print["Verification lengths: ", 
  np  ArcLength[
     RotationMatrix[\[Theta]].({t, eq[t]}), {t, -a, u /. Last@sol}]/
    circ, " =?= k=", k];

This is true for the Good ellipse and false for the Bad one, because the "cut points" are ill-placed: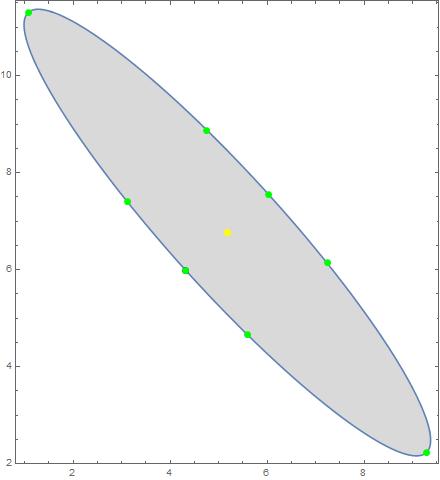

What is wrong with TourCir? I join the complete notebook.

Attachments:

SampleEllipse.nb