My research lab has used Mathematica for many years developing models for fuel cells and simulating signals we expect from experimental measurements. Many of these files were created in version 9.0 and I have been running version 11.0.1 on my personal laptop. I updated to version 12 today and the code is giving a different output from a Fourier Transform. Specifically, it is a Fourier transform of a cosine that is multiplied by a Gaussian window function and a rectangular window function. From the revision history, it seems the FourierTransform function was last changed in version 11.2.

All of this is shown in the attached file, but I will also repeat here for easy viewing. A few variables that need to be explained, ft= applied frequency, k= harmonic index, b= Gaussian window parameter, Cyc= number of signal waveforms, and nt= number of samples.

The cosine is defined by: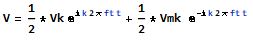
Where Vk and Vmk are complex coefficients as:
The Gaussian window function is defined as: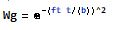

The rectangular window function is defined as: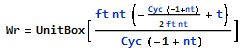

Finally, we take the Fourier transform of the windowed signal:

The (presumably correct) answer from Versions older than 11.2 is: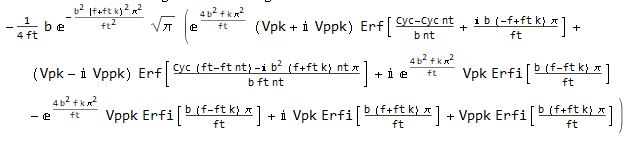

But the answer I'm getting now is: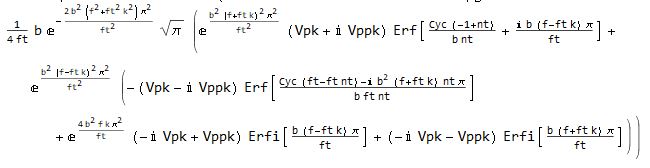

Using SameQ confirms these equations aren't equivalent. I've tinkered with the Fourier Parameters a bit, but that only seems to change the scaling coefficients. One obvious solution is reverting to pre-11.2, but I would like to avoid being stuck to a past version. Thank you in advance!

Update: The apparent errors stemmed from changes in how Mathematica handles variable precisions and underflow. Using some workarounds from @Valerio in Q170416 and @halirutan in Q69912 I've updated my notebook to a working version. I would, however, appreciate if anyone knows of more elegant solutions than what I implemented. Thank you again!

Attachments:

Fourier Transfor...nb

Fourier Transfor...nb